插值与逼近混合的三重细分法

檀结庆，朱星辰，黄丙耀，蔡蒙琪，曹宁宁

（合肥工业大学数学学院，安徽合肥230601）

细分是一种构造光滑曲线曲面的有效方法，由于其具有算法简单、易于实现的优点，被广泛运用于计算机辅助几何设计、计算机图形学、动漫制作等领域。通常分插值型细分和逼近型细分2种。插值型细分的极限曲线曲面精确地经过所有控制顶点，逼近型细分的极限曲线曲面通常不通过控制顶点。 插值型细分方便形状控制，DYN等［1］提出了经典的四点插值细分法，并证明了生成的极限曲线是C1连续的。DESLAURIERS 等［2］利用插值多项式得到了2n点b重细分法。 HASSAN等［3］构造了C2连续四点三重插值细分格式。在曲面情形，KOBBELT［4］提出了任意拓扑结构开四边形网格上的插值细分法。DYN等［5］构造了三角形网格上的一种蝶形细分法。 LI等［6］在Kobbelt插值细分法的基础上进行改进，提出了一种新的插值型细分法，其正则情形与Kobbelt细分保持一致。相关理论被推广到三重曲面细分，LI等［7］提出了插值三重曲面细分法。另一方面，逼近型细分可以达到高阶连续，HASSAN等［8］构造了三点三重逼近细分格式，SIDDIQI等［9］提出了极限曲线可以达到C6连续的逼近细分格式。 LANE等［10］指出对控制多边形进行局部平均操作可以得到任意次均匀B-样条。 将其推广到曲面情形，STAM［11］提出了生成任意次均匀B-样条曲面的细分法。类似方法运用到三角形网格，OSWALD等［12］提出了细分法。然而，存在一类带参数的混合细分格式，通过参数的不同取值，该细分既可以成为插值型细分又可以成为逼近型细分。郑红婵等［13］将单参数的四点插值细分法扩展为双参数四点二重细分法，既能构造光滑插值曲线，又能构造光滑逼近曲线。PAN等［14］利用松弛技术将插值型细分和逼近型细分相结合，构造了一类C2连续的插值与逼近型细分相结合的细分格式。檀结庆等［15］在插值细分法中引入偏移变量，提出了基于插值细分的逼近细分法。 REHAN等［16］给出了组合型四点三重细分格式。 NOVARA等［17］对组合型四点三重C2和C3收敛的范围进行了完整的描述。关于曲面情形，MAILLOT等［18］介绍了用push-back操作来渐进插值控制点。文献［19-20］通过逼近型细分来构造插值型细分。

本文提出了一种新的四点三重插值曲线细分法和一种含参数的三次B-样条曲线细分法，基于此得到了一种插值与逼近相混合的三重曲线细分法。这种混合细分法使得插值细分和逼近细分统一为同一格式。本文将这种方法推广到曲面曲线，提出了四边形网格上的1-9插值曲面细分法和张量积三次B-样条曲面细分法，利用提出的插值曲面细分法和张量积三次B-样条曲面细分法，得到了一种插值与逼近相混合的三重曲面细分法。

1 三重曲线细分法

1.1 新的四点三重插值曲线细分法

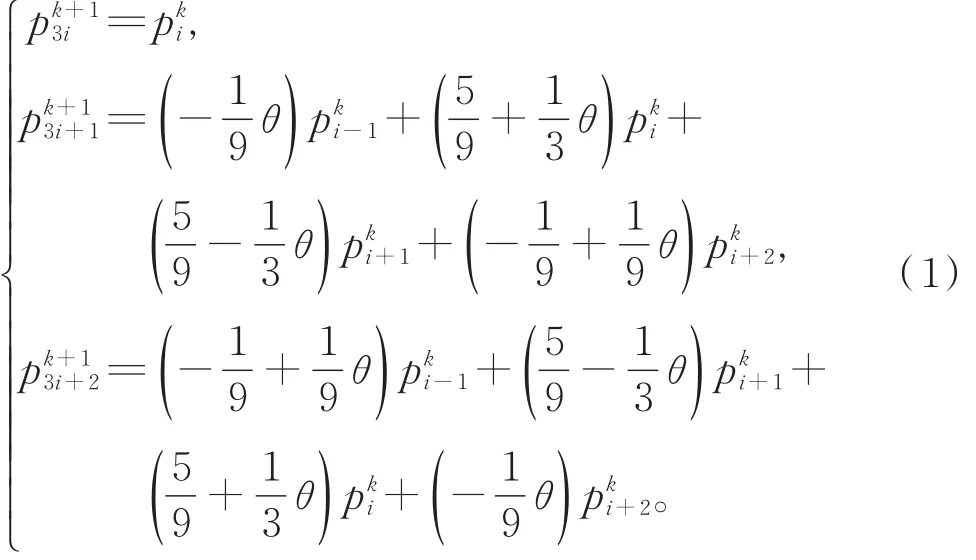
1.2 含参数的三次B-样条曲线细分法

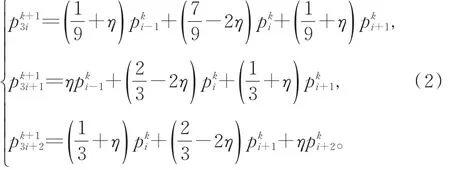
1.3 插值与逼近混合的三重曲线细分法

令

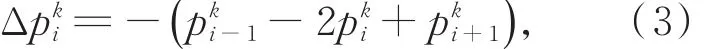
式（1）可改写为

式（2）可改写为

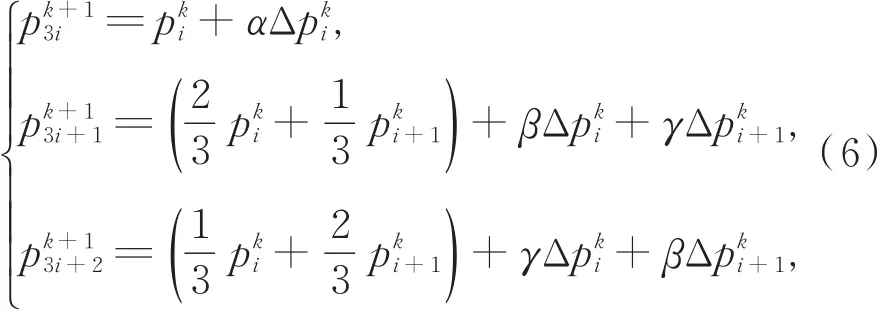
构造示意图见图1。插值与逼近混合的三重曲线细分格式定义如下：

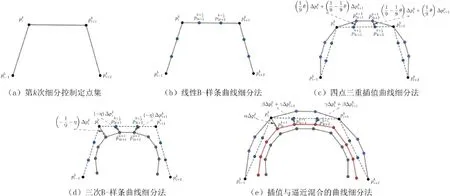
图1 构造混合三重曲线细分法的几何示意图Fig.1 The geometric sketch of constructing blending ternary subdivision scheme

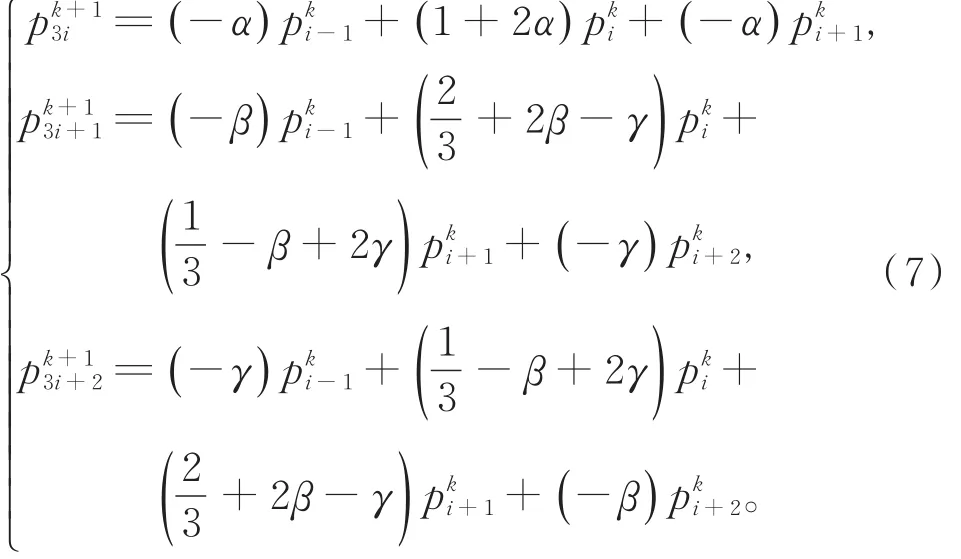
注2 当α=0时，式（7）为插值型曲线细分格式；当α≠0时，式（7）为逼近型曲线细分格式。 特别地，当时，式（7）为D-D四点三重插值格式；当时，式（7）为Hassan四点三重插值细分格式；当α=0，β=0，γ=0时，式（7）为线性B-样条细分格式；当时，式（7）为二次B-样条细分格式；当时，式（7）为三次 B-样条细分格式；当时，式（7）为四次 B-样条细分格式。

定理1 插值与逼近混合的三重曲线细分法可以达到C3连续。

证明 插值与逼近混合的三重曲线细分格式（7）的掩模

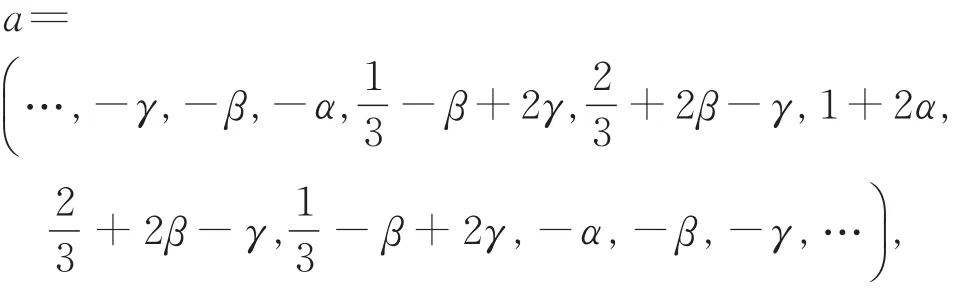
生成的多项式为

易知式（7）的j(j=1,2,3,4)阶差商格式的掩模为

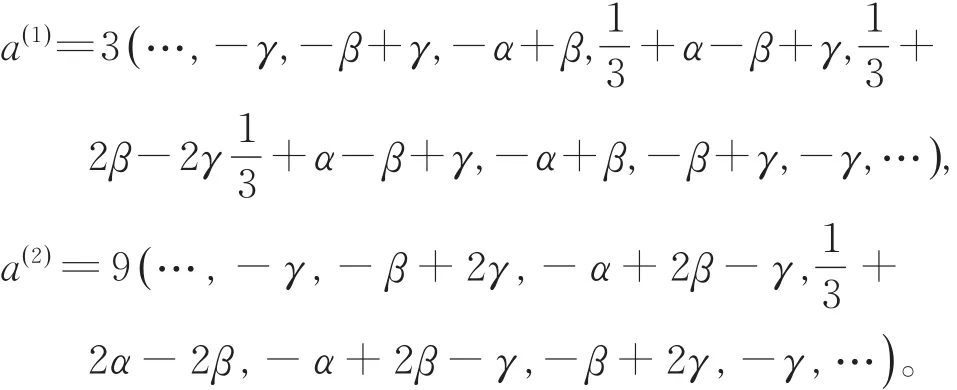
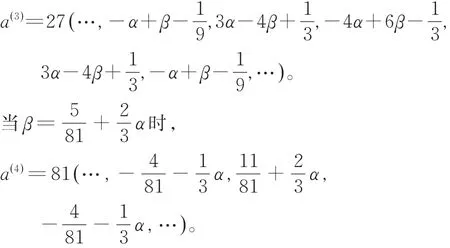
可得

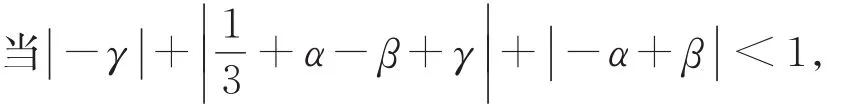
式（7）是C2连续的；

2 三重曲面细分法

2.1 四边形网格上的四点三重插值细分法

基于1.1节新的四点三重插值曲线细分法，本节将其推广到曲面情形，得到正则四边形网格上的1-9插值细分法。

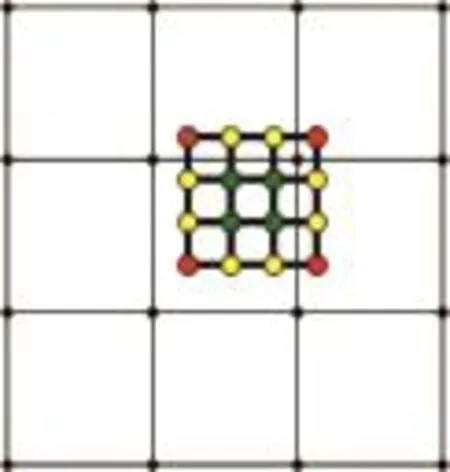
给定初始控制网格P0，设Pk为第k次细分后得到的正则四边形网格，其上的一个4×4子网格

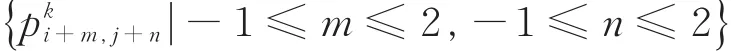
如图2所示，定义1-9插值细分规则如下：

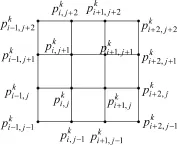
图2 正则四边形网格Pk的一个4×4子网格Fig.2 A4×4sub-mesh of the regular quadrilateral mesh

新顶点的生成规则为

新边点的生成规则为

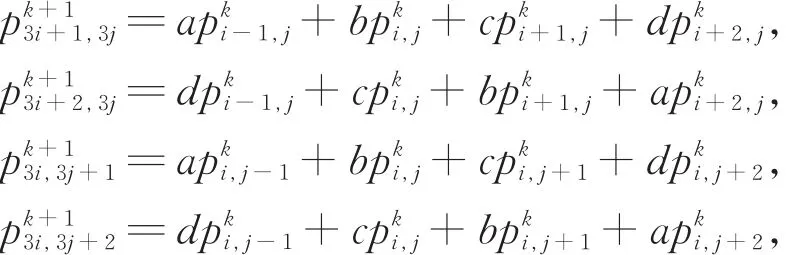
生成的示意图见图3。

新面点的生成规则为

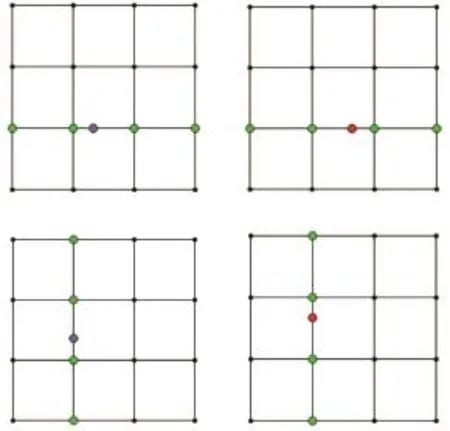
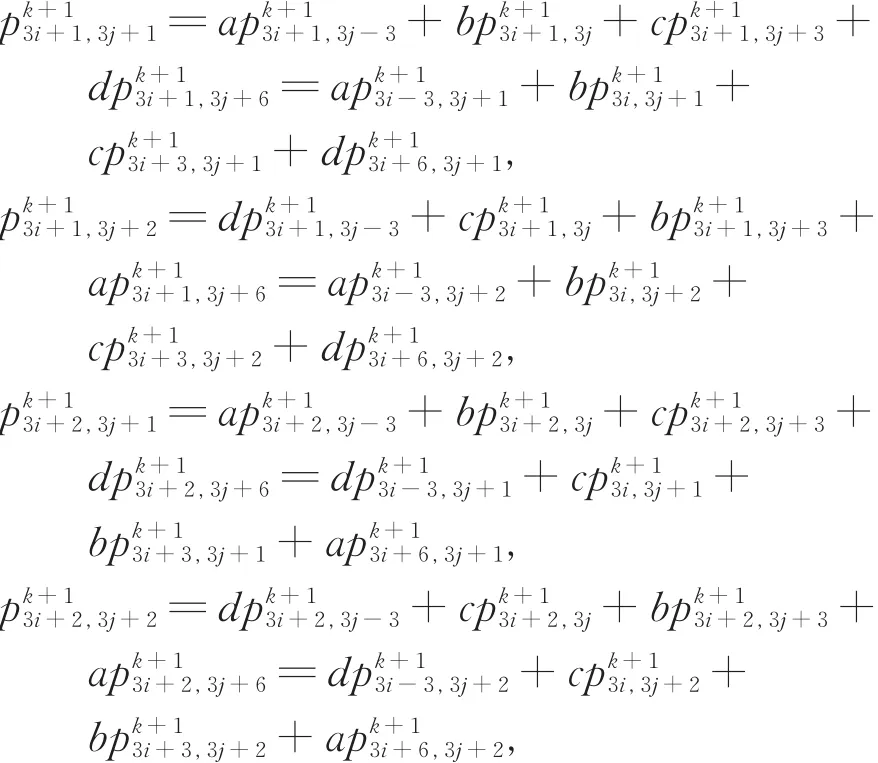
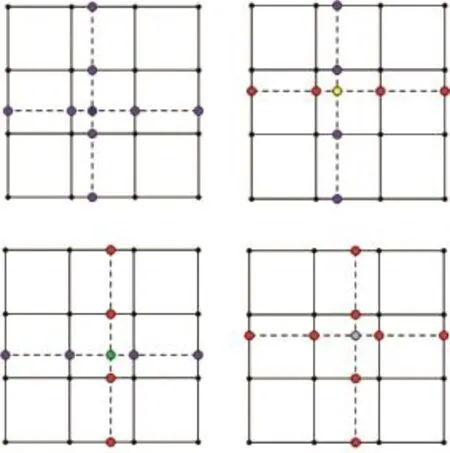
图4 生成新面点的示意图Fig.4 The sketch of computing new face vertices

从而一个四边形格子分为9个四边形格子，见图5，即为1-9插值细分法。

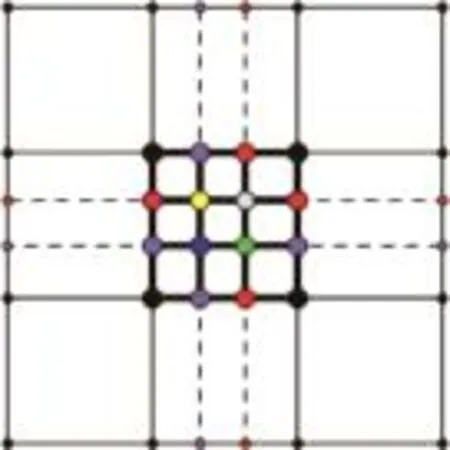
图5 1-9插值细分法Fig.5 The 1-9 interpolating subdivision scheme

2.2 张量积三次B-样条细分法

基于1.2节含参数的三次B-样条曲线细分法，本节将其推广到曲面情形，得到张量积三次B-样条曲面细分法。

给定初始控制网格P0，设Pk为第k次细分后得到的正则四边形网格。

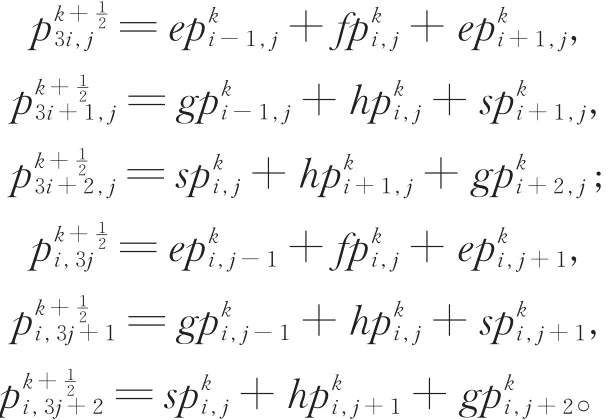
新顶点的生成规则为

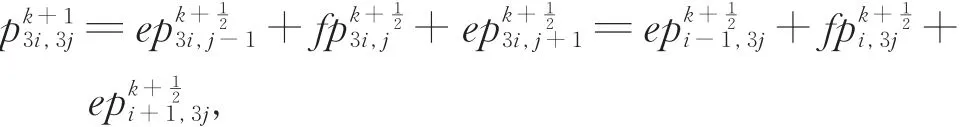
生成的示意图见图6。

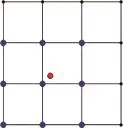
新边点的生成规则为

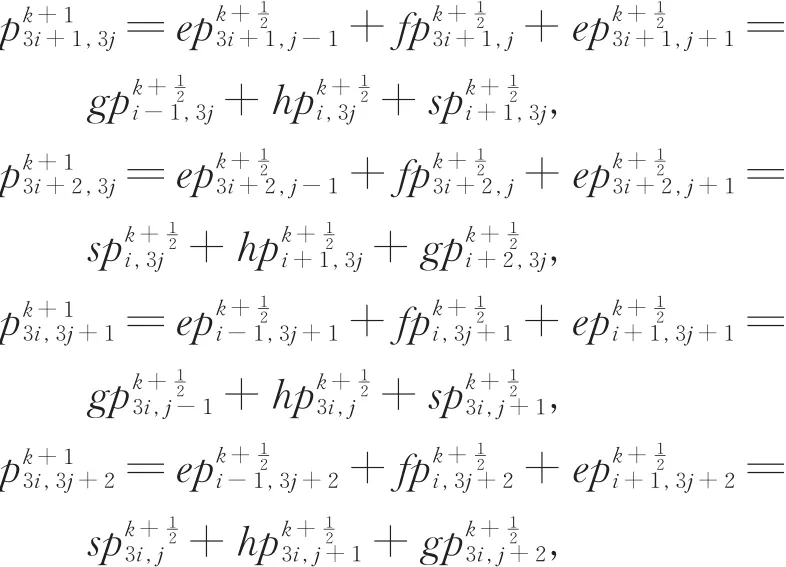
生成的示意图见7。

新面点的生成规则为

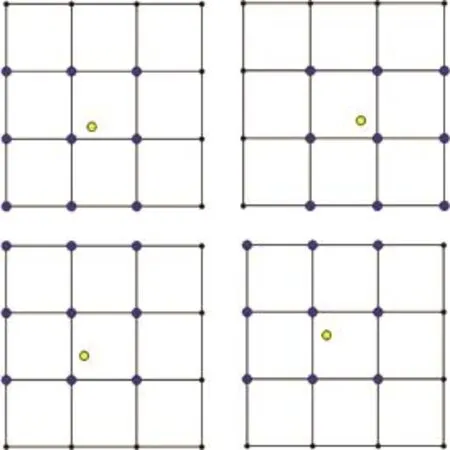
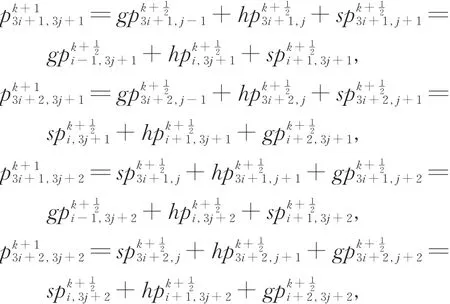
生成的示意图见8。

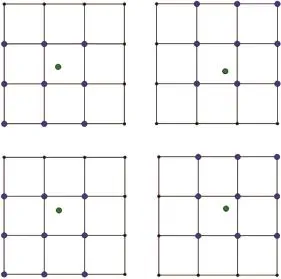
如此得到了张量积三次B-样条细分法，见图9。

2.3 插值与逼近混合的三重曲面细分法

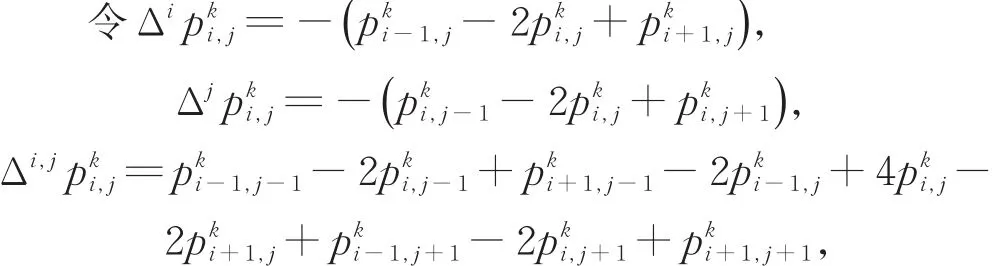
给定初始控制网格P0，设Pk为第k次细分后得到的正则四边形网格，插值与逼近混合的三重曲面细分规则定义如下：

新顶点的生成规则为

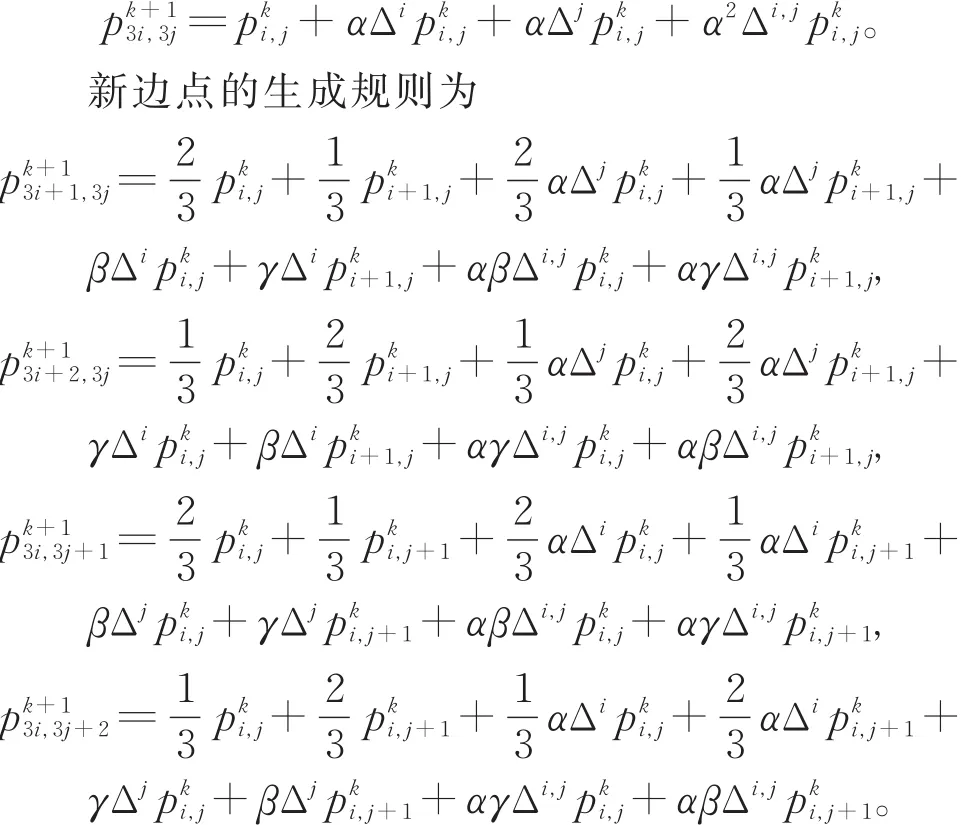
新面点的生成规则为

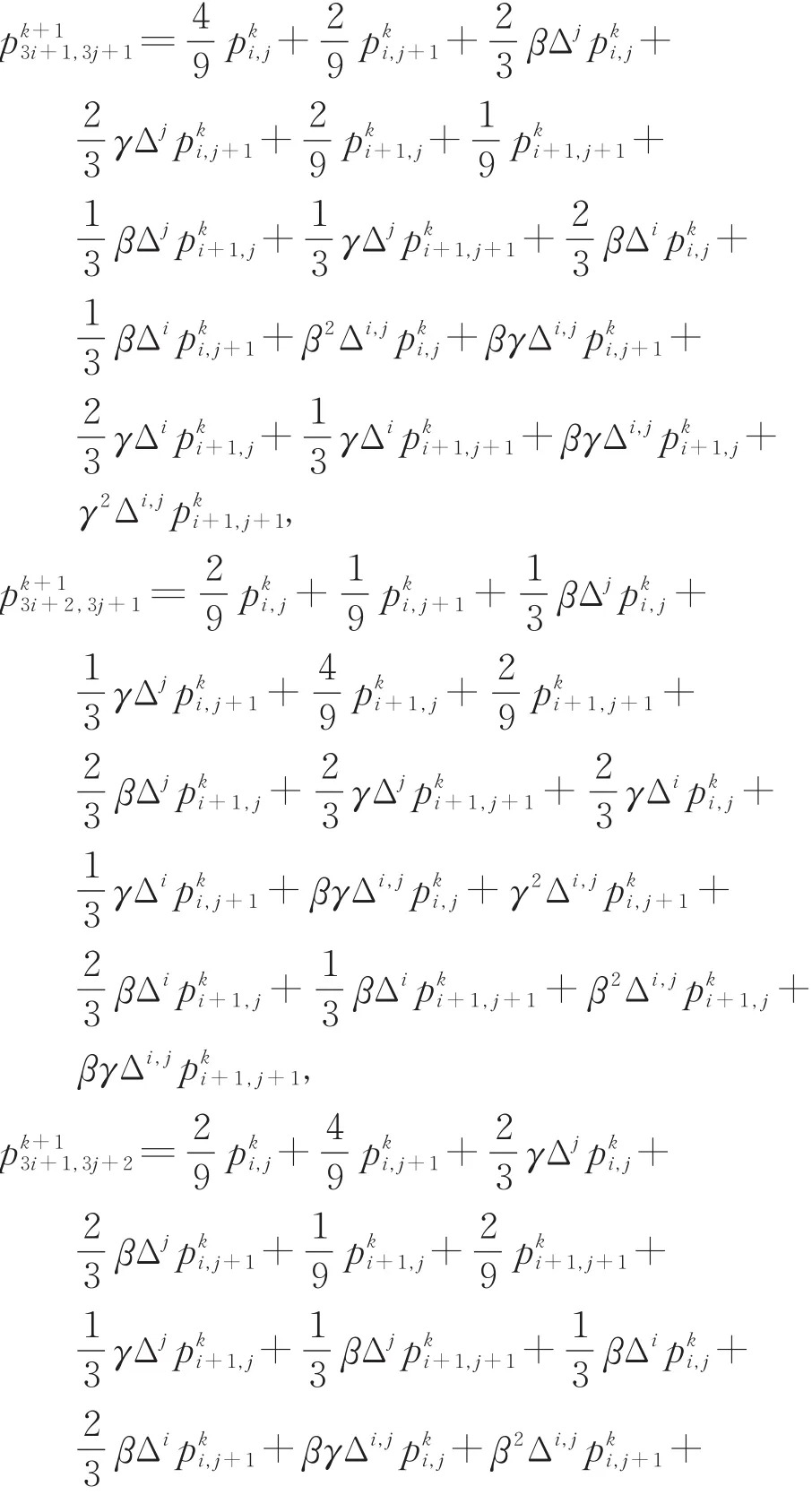
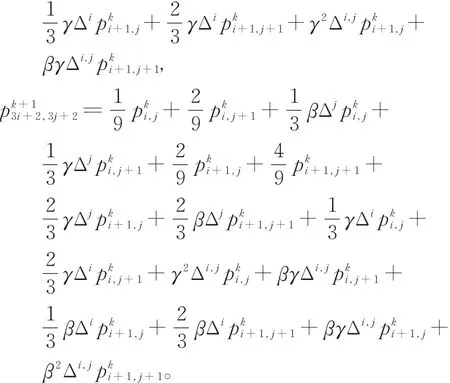
注3 当α=0时，得到插值型曲面细分法；当α≠0时，得到逼近型曲面细分法。特别地，当时，得到第2.1节1-9插值曲面细分法；当时，得到第2.2节张量积B-样条曲面细分法。

定理2 插值与逼近混合的三重曲面细分法可以达到C3连续。

证明 由定理1知，插值与逼近混合的三重曲面细分法的生成多项式为式（8），

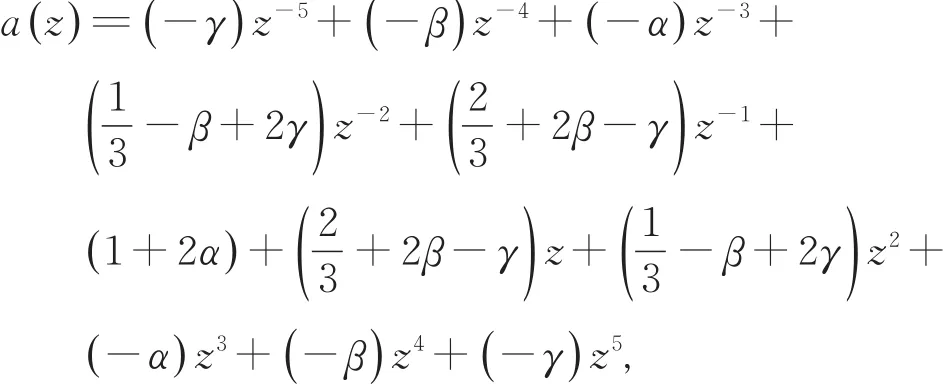
则由张量积形式推广得到的插值与逼近混合的三重曲面细分法的生成多项式为

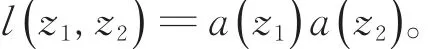
易知，

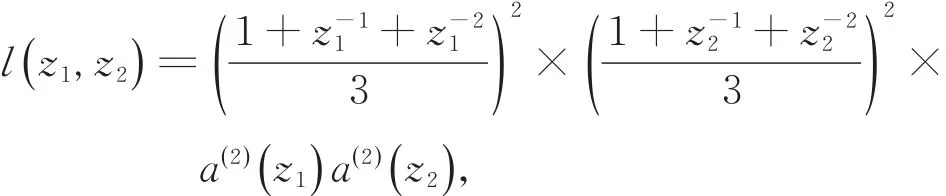
其中，

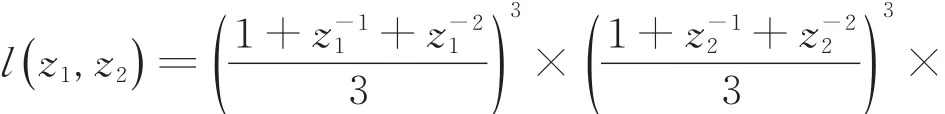
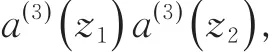
其中，

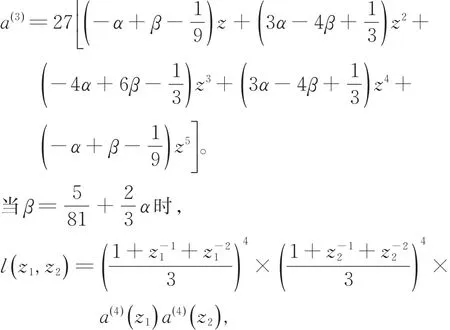
其中，

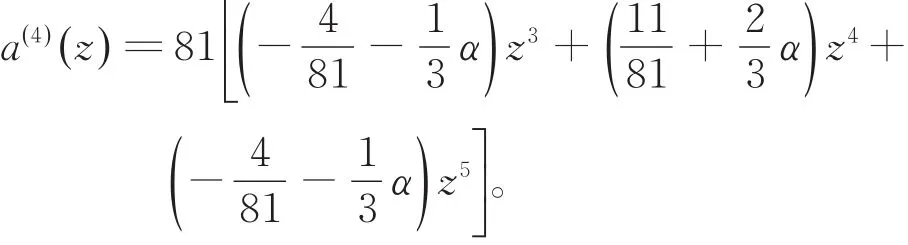
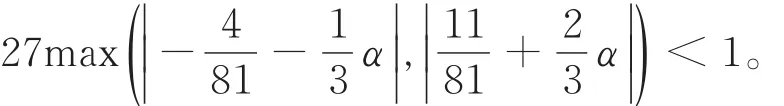
3 数值实例

利用四点三重插值曲线细分法和三次B-样条曲线细分法得到了一种插值与逼近混合的三重曲线细分法。这种混合细分法使得插值细分与逼近细分统一为一个格式。将此方法推广到曲面情形，提出四边形网格上一种1-9插值曲面细分法和一种张量积B-样条曲面细分法，利用此两种曲面细分法得到了一种插值与逼近相混合的三重混合曲面细分法。这些混合细分法所生成的极限曲线曲面，能同时达到插值细分法和逼近细分法生成曲线曲面的效果。其中，参数的取值决定了极限曲线曲面的形状。在给定初始控制顶点集的情况下，可通过选择适当的参数来调整和控制曲线曲面。图10～图13为利用本文方法生成的极限曲线曲面的数值实例。

图10为在给定初始控制顶点下分别由插值细分法和逼近细分法生成的极限曲线。其中，（a）为新的四点三重插值曲线细分格式（1）在时生成的极限曲线；（b）为含参数的三次B-样条曲线细分格式（2）在时生成的极限曲线。

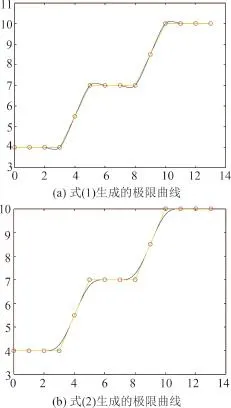
图10 由插值细分法和逼近细分法生成的极限曲线Fig.10 Limit curves generated by interpolating subdivision scheme and approximating subdivision scheme

图11显示的是当初始控制多边形为正六边形时，插值与逼近混合的三重曲线细分格式（7）中α,β,γ取不同值时对极限曲线的影响。 其中，（a）所示的极限曲线与控制多边形完全重合，此时，

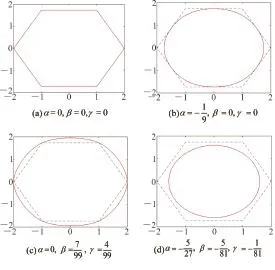
图11 参数取不同值时，式（7）生成的极限曲线Fig.11 Limit curves generated by the formula（7）when the parameter takes different values

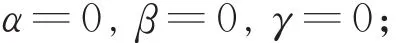
（b）所示的极限曲线与控制多边形相切，此时，

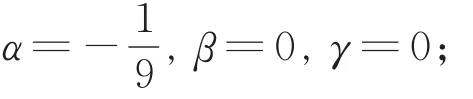
（c）所示的极限曲线精确地通过控制顶点，此时，

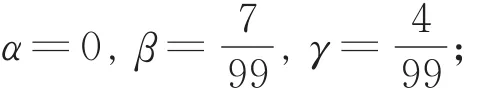
（d）所示的极限曲线逼近控制多边形，此时，

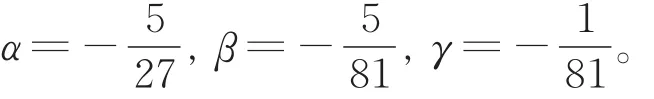
图11足以说明，混合型三重曲线格式（7）既可生成插值型极限曲线，也可生成逼近型极限曲线；适当选取参数可控制极限曲线的形状。

在给定的初始控制网格下分别由插值细分法和逼近细分法生成的曲面如图12所示。其中，（a）为初始控制网格；（b）为当时，四边形网格上的四点三重插值细分法细分2次后生成的曲面；（c）为细分3次后生成的极限曲面；（d）为当时，张量积B-样条曲面细分法细分2次后生成的曲面；（e）为细分3次后生成的极限曲面。

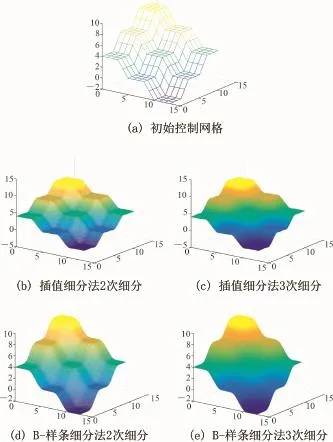
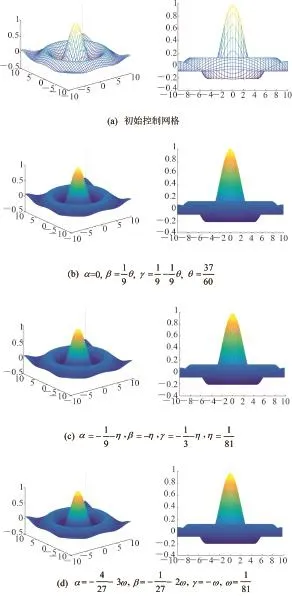
图13为在给定初始控制网格时，插值与逼近混合的三重细分法生成的曲面。其中，（a）为初始控制网格；（b）为当时生成的 极 限 曲 面 ；（c）为 当时生成的极限曲面；（d）为当α=时生成的极限曲面。

4 结 论

给出了一种新的四点三重插值曲线细分法和一种含参数的三次B-样条曲线细分法，基于此得到了一种插值与逼近相混合的三重曲线细分法。这种混合细分法使得插值细分和逼近细分统一为同一格式。本文将这种方法推广到曲面曲线，提出了四边形网格上的1-9插值曲面细分法和张量积三次B-样条曲面细分法，利用提出的曲面细分法，得到了一种插值与逼近相混合的三重曲面细分法。证明了其极限曲线曲面可以达到C3连续，较于文献［12-17］提出的细分法生成的极限曲线，具有更高的连续性。最后，用数值实例说明各参数对极限曲线曲面的影响。未来，笔者将进一步研究混合型细分法，得到更高阶连续与其他优良性质相统一的细分格式，探究非正则网格上的曲线曲面细分法。