浅谈在卡诺图中实现对偶律的方法
姜书艳 张优 卢有亮 刘科 张博

摘要:应用卡诺图来处理逻辑函数可以方便快速地使函数化简或变形。本文基于逻辑代数中的对偶律和卡诺图的化简方法,提出了在卡诺图中实现对偶律的方法:定义法,公式法,反码法。不同方法简单程度不同,反码法最为简便。
关键词:逻辑代数;对偶律;卡诺图;反码
中图分类号:G642.0 文献标志码:A 文章编号:1674-9324(2019)12-0219-02
对偶律在逻辑代数中有着非常广泛的应用。任何一个逻辑函数,都有它对应的对偶式。逻辑代数中的公式都是成对出现的,每个公式的对偶式都是成立的。这使得我们在学习逻辑代数时,只需掌握一半的公式即可用对偶律得到另一半公式,大大减少了我们的工作量。在实际应用中,正逻辑约定和负逻辑约定互为对偶关系,所以对偶律在逻辑电路中也有着很大作用。
文献1仅给出了公式法对卡诺图实现对偶律的问题的解决,较为烦琐。文献2中提出了新的概念“对偶卡诺图”,并应用它来化简最大项相与的逻辑表达式。该方法是将对偶律应用在了整个卡诺图化简的所有步骤中,对直接化简最大项相与的逻辑表达式较为有用。然而我们对最大项相与的逻辑表达式可以先对偶为最小项相或的逻辑表达式,然后使用传统方法进行化简,这样更为简单。基于以上文献的启发,本文给出卡诺图法实现对偶律的方法。
一、对偶规则
对偶规则:对于任何逻辑函数表达式Y,如果将式中所有的符号“·”换成“+”,“+”换成“·”,“1”换成“0”,“0”换成“1”,并不改变原来的运算次序,则得新的逻辑函数式YD,YD是Y的对偶式。同样,Y也是YD的对偶式。例如,F=(A+B+C)(A+B+C)(A+B+C)的对偶式为FD=ABC+ABC+ABC。该对偶规则可对公式进行化简。
二、在卡诺图中实现对偶律
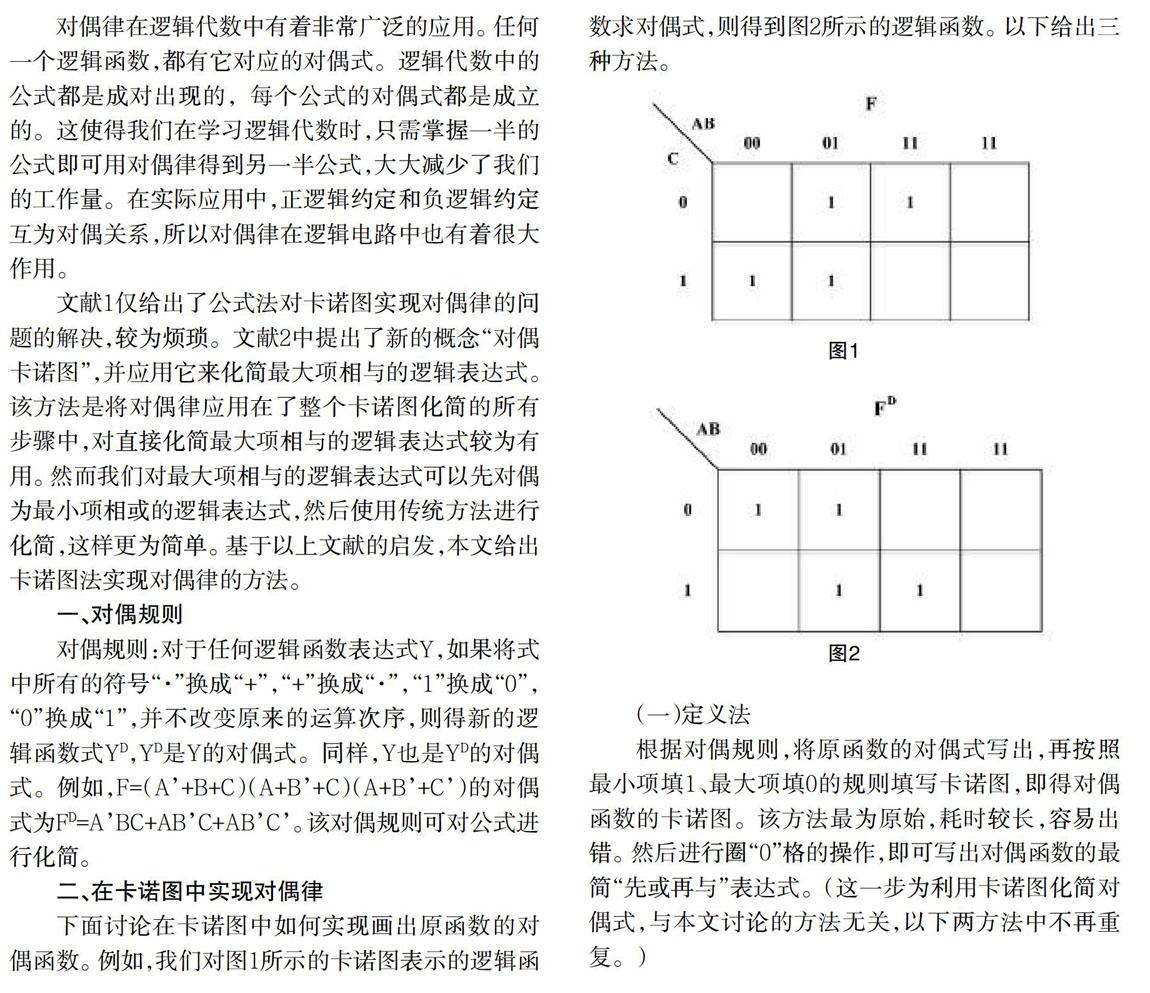
下面讨论在卡诺图中如何实现画出原函数的对偶函数。例如,我们对图1所示的卡诺图表示的逻辑函数求对偶式,则得到图2所示的逻辑函数。以下给出三种方法。
(一)定义法
根据对偶规则,将原函数的对偶式写出,再按照最小项填1、最大项填0的规则填写卡诺图,即得对偶函数的卡诺图。该方法最为原始,耗时较长,容易出错。然后进行圈“0”格的操作,即可写出对偶函数的最简“先或再与”表达式。(这一步为利用卡诺图化简对偶式,与本文讨论的方法无关,以下两方法中不再重复。)
在上例中,我们写出F的逻辑表达式,F=ABC+ABC+ABC+ABC,用卡诺图化简后为F=BC+AC,写出原函数的对偶式,为FD=(A+B+C)(A+B+C)(A+B+C)(A+B+C)。其中(A+B+C)在真值表中对应101,所以在卡诺图中ABC对应101的格子填0,其他最大项的填法以此类推,即得图2所示的卡诺图,用卡诺图化简表达式后FD=(B+C)(A+C)。
(二)公式法
首先,由原函数的卡诺图获得其全部最小项编号(即原函数卡诺图中的1格所对应编号)。用(2n-1)减去这些编号(n为函数变量个数),由此获得对偶式的全部最大项的编号,填出对应的卡诺图即可。此方法即为文献1所提到的方法,对于每一项的编号都需要进行一次运算,其间还要进行二进制与十进制的转换,较为烦琐。该方法原理如下:一个n变量函数的最小项mi,其对偶为:(mi)d=(*)那么对偶式中的最大项与原函数中的最小项一一对应,其关系为:若原函数中最小项编号为i,则对偶函数中有编号为(2n-1)-i的最大项(n为函数变量个数)。
在上例中,我们写出F的逻辑表达式,F=ABC+ABC+ABC+ABC,用最小项之和表示为FD=(A+B+C)(A+B+C)(A+B+C)(A+B+C),用卡诺图化简后为FD=(B+C)(A+C)。
(三)反码法
不难注意到,公式法中公式(*)的下标之和为2n-1,这与我们求反码的方法极为相像。我们只要将卡诺图中每一个方格所对应的二进制数取反码,在对应的格子中填入相应的逻辑值,原来是0的对应的填1,原来是1的对应的填0即可。例如,原函数中000对应的格子填的是0,那么我们应该在对偶式中111对应的格子中填1。其他格子的填法以此类推。此方法最为简便。该方法原理如下:在用二进制表达最小项时,我们把原变量写为1,反变量写为0。比如对于ABC这样的最小项,我们用二进制表达为101,它在卡诺图中对应的二进制也为101。而在用二进制表达最大项时,我们把原变量写为0,反变量写为1,与最小项的表达就是反码关系。比如,对于ABC的对偶A+B+C这样的最大项,我们用二进制表达为010,恰恰与原式的101形成反码关系。
在上例中,我们写出F的逻辑表达式,F=ABC+ABC+ABC+ABC,它的最小项用二进制原码表示为001,010,011,110。对每一项取反码之后,得到110,101,100,001,在它的对偶式的卡诺图中对应的填上0,得到对偶函数为FD=(A+B+C)(A+B+C)(A+B+C)(A+B+C),用卡诺图化简后为FD=(B+C)(A+C)。
三、结论
本文提出的三种方法都可以在卡诺图中实现對偶律,不同方法简单程度不同。定义法直接按照对偶规则写出对偶式再填卡诺图,最为原始,耗时较长,容易出错。公式法利用原函数的最小项和对偶式的最大项之间的和不变关系,对于每一项的编号都需要进行一次运算,其间还要进行二进制与十进制的转换,较为复杂。反码法只需对填1的格子对应的二维码取反码,并在新图中填0即可。相比之下反码法最为简便。
参考文献:
[1]徐兵,朱鹏远.基于卡诺图在处理逻辑函数方面的应用研究[J].昌吉学院学报,2010,(3):96-98.
[2]張迎.反演卡诺图和对偶卡诺图[J].湖州师专学报,1996,(6):31-35.
[3]姜书艳.数字逻辑设计及应用[M].电子科技大学出版社,2014.
[4]王诗兵,黄正杰.关于卡诺图法实现逻辑函数变换的研究[J].安徽职业技术学院学报,2005,(4):5-7.
[5]陈小芳.逻辑函数的卡诺图化简法[J].计算机时代,2010,(8):49-51.
[6]罗嘉庆,周世杰,徐洁.原码、反码和补码的教学探讨[J].计算机教育,2015,(10):42-45.
The Methods to Apply Duality Theorem in Karnaugh Map
JIANG Shu-yan,ZHANG You,LU You-liang,LIU Ke,ZHANG Bo
(University of Electronic Science and Technology of China,Chengdu,Sichuan 611731,China)
Abstract:Using Karnaugh map to deal with logic functions can simplify and transform logic functions fast and conveniently.The paper presents some methods to apply Duality Theorem in Karnaugh map,based on Duality Theorem in Logic Algebra and simplification method of Karnaugh map.The level of complexity varies from methods to methods.Among definition method,formula method,ones'- complement method,ones'- complement method is the simplest and most convenient one.
Key words:logic algebra;duality theorem;Karnaugh map;ones'- complement

