联合有限元法及其收敛性与精度分析

卿光辉，王博鳌

（中国民航大学航空工程学院，天津 300300）

协调位移有限元法采用了一般线性协调位移元的插值多项式，但其位移结果和应力结果的收敛速度相对较差，并存在自锁问题，而非协调位移项的引入[1-2]是改善该问题的有效方法。其次，位移法通常需利用本构关系来计算应力，由于应变-位移是微商关系，也是应力结果精度不如位移结果的原因之一。另一种单变量有限元法是基于最小余能原理的应力法，由于应力平衡元要求在张量空间中建立所需的平衡关系和正则条件都比较困难，使其并没有得到充分的发展。为了解决该问题，卞学鐄[3]于1964年从最小余能原理出发，通过拉格朗日乘子法（也可直接用H-R变分原理）建立了杂交应力有限元方法。杂交应力元的思想是保持单元内部应力的平衡，但放松了正则条件，其结果比位移法更好，且在解决体积剪切自锁问题和不可压缩材料问题上有一定的优势。但杂交应力元法为了实现位移法求解，要先对应力场变分后得到欧拉方程，利用其消去应力变量，再对位移变量变分，才能得到位移与外载荷的关系方程，因而要求对单元级的矩阵求逆。另外，杂交应力元的应力模式选择比较烦琐。

混合法是包含两类或两类以上变量的有限元方法。Herrmann[4]和Qukit等[5]最早用该方法分析板壳问题。很多学者针对混合法中不正定线性方程组的求解问题有一定研究[6]。用混合法分析板壳问题，最明显的优势是应力结果精度高，且收敛速度快，但一般混合法涉及多类变量时，对计算机的性能要求较高，计算效率不如单变量位移法。另一方面，在网格较粗的情况下，以一般插值多项式表达位移和应力变量的混合法数值结果存在较明显的振荡现象[6]。

文献[7]在“保辛”理论[8-9]的指导下，从修正的H-R变分原理出发，建立对偶变量块体混合元，该方法实质上也是位移法，但与杂交应力元法不同，没有应力模式的选取要求。

根据文献[7]的理论背景和构建过程，目前的方法可简称为联合有限元法。该方法以修正的H-R变分原理和势能原理为基础，建立线形求解方程，避免通过本构关系求解应力变量，从而提高应力计算精度、收敛度及计算效率。同时，不用放松正则条件及应力模式的选取，理论上更加严谨。通过数值算例，与ABAQUA的计算结果进行对比分析，该方法具有一定优越性。

1 理论分析

1.1 修正的H-R变分原理与部分混合元列式

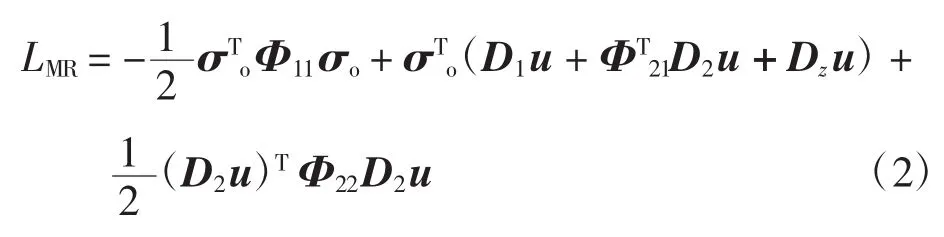
其中：σo=[σxzσyzσzz]T为平面外应力；Φ11、Φ21和 Φ22为材料参数矩阵；D1，D2和Dz为微分算子矩阵，即

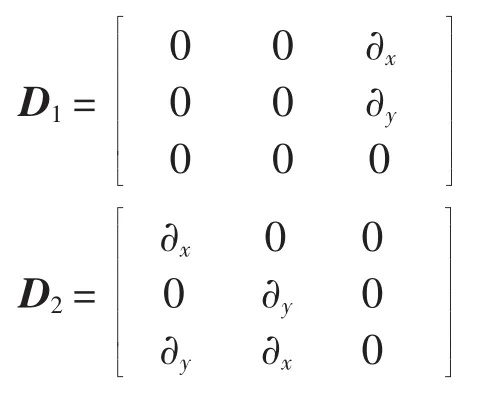
平面内应力可由平面外应力变量和位移变量表示为

为了实现结点上位移与平面外应力均“保辛”[10-11]的目标，应坚持求解各类变量的系数矩阵对称原则。设平面外应力σo和位移u在空间域内离散后的表达式为

其中：pe=[σexzσeyzσezz]T；qe=[uevewe]T；N=diag（NeNeNe），Ne为单元各结点组成的向量，Nei=（1+ξiξ）（1+ ηiη）（1+ ζiζ）/8。

将式（4）和式（5）代入式（1）可得

其中

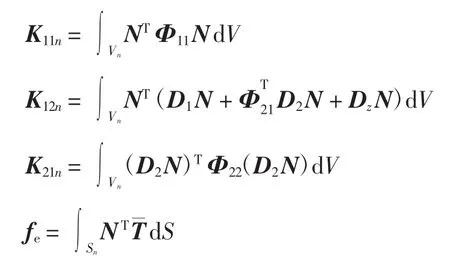
将pe和qe视为相互独立的变量，则由δΠMR（pe，qe）=0得到欧拉方程如下

文献[7]用以下公式消除欧拉方程（8）的应力与位移的耦合关系，即

将式（9）代入式（8）中，可得

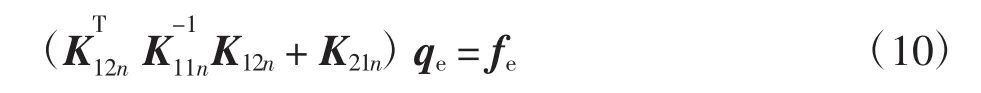
实际上，式（9）包含了对单元级的K11n求逆。在网格数增加或单元类型的单元结点数较多时，如20结点实体元，计算效率会明显下降。同时，也假设势能原理的位移条件事先满足u-=0，即

其中：D为通常位移法中的算子操作矩阵；C为材料本构关系的系数矩阵。

假设式（11）和式（1）是对同一工程结构静力学问题的表述。将式（5）代入式（11）中，有

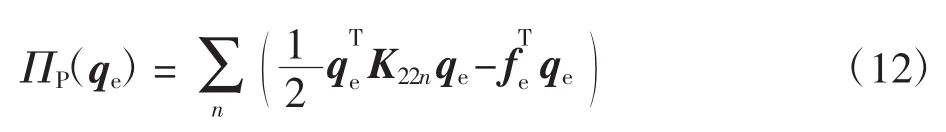
则将式（13）替代式（8），得到了关于位移变量和平面外应力变量的单元列式如下

对式（14）或式（15）两边分别求和，则问题的控制方程分别为

其中：K11= ∑K11n；K12= ∑K12n；K22= ∑K22n；p= ∑pe；q=∑qe；f= ∑fe。

与位移法同样，可先通过式（17）独立求位移的解，然后将结果代入式（16）求解平面外应力。

从以上理论的推导和最终的单元列式（14）和式（15）的形式来看：联合有限元法避免了通过较为繁琐的式（10）求解位移变量，采用较为简便的位移法求解，从而提高了计算效率；在求解应力时，没有采用计算精度较低的本构关系进行求解，而通过修正的H-R变分原理中应力计算公式计算出应力结果；将两个方程通过线形方程组形式进行同时求解，又进一步提高了计算效率。此方法可称由H-R变分原理和势能原理的欧拉方程联合得到的单元列式（14）和式（15）为联合单元列式（CEF）。

1.2 应力求解方法

1.2.1 平面外应力的求解方法

对于以联合单元列式（14）为基础的控制方程（16）来说，系数矩阵K11是对称“保辛”的。同时，与求解位移相同，便于施加平面外应力边界条件，确保了边界结点上的结果与事先给定的应力数值一致。

1.2.2 平面内应力的线性方程组方法

为了便于平面内应力边界条件的引入，可进一步考虑具体结构中同一材料的线性方程组形式。将式（4）和式（5）代入式（3）中，然后两边求和，可分别构建关于同一材料平面内应力的线性方程组为

其中：K=∑In，In是24×24的单位矩阵（假设是8结点块体元）；pi为待求的平面内应力向量；Γ=∑（Φ21pe+Φ22（DzN）qe），（DzN）矩阵需根据具体等参坐标（ξ，η，ζ）的位置代入-1，0，1 等值。构造式（18）时无需数值积分，速度快。

需进一步说明以下两点：一方面，式（18）中K只有主对角线上存在元素，理所当然对称“保辛”。另一方面，构建式（18）的前提条件是同一材料的单元必须连续（如呈层状的复合材料结构中的同一材料层）。

1.3 非协调位移联合元

根据文献[1-2，15-16]中非协调位移元法，可将位移插值表达式分为协调部分和非协调部分，即

将式（19）代入式（11）后有

对式（20）求和可得

将K′22替代式（17）的K22可得非协调位移元的方程。联合有限元方法的非协调元计算代码采用了文献[16]的理论公式。由于式（14）中的系数矩阵与式（15）的刚度矩阵相比较柔[4-5]，故没有考虑式（14）的非协调形式。

2 数值算例

已知矩形板的长和宽a=b=1.0，厚度H=0.1。材料参数[17]为 E11=10E22=10E33，G12=G13=0.6E33，G23=0.5E33，μ12= μ13= μ23=0.25。板上表面（z=0.1）受垂直向下的均布载荷q=1作用，四边简支（SSSS）。

计算程序中，每一坐标方向采用两点高斯积分。网格为12×12×4的四分之一模型，在同一台集成4核（3.2 GHz）的机器上运算，联合有限元法用时3.6 s，而文献[7]中的方法用时4.2 s。

在以下的数据对比曲线图中，8结点协调联合元简称CCFEM8，非协调联合元简称NCCFEM8，ABAQUA的8结点非协调位移元，简称NC3D8，各计算结果均进行了无量纲化处理。

图1～图6中横坐标序号与网格划分密度对应关系如表1所示，其中，网格划分密度为长×宽方向的单元数，厚度方向网格划单元数均为4。图7和图8给出沿着厚度方向应力σxy′和σyy′分布及对比结果，其中横坐标为沿着厚度方向的坐标。

图1 u′与精确解比较Fig.1 Comparison between u′and exact solution

图2 w′与精确解比较Fig.2 Comparison between w′and exact solution

图3 σxz′与精确解比较Fig.3 Comparison between σxz′and exact solution

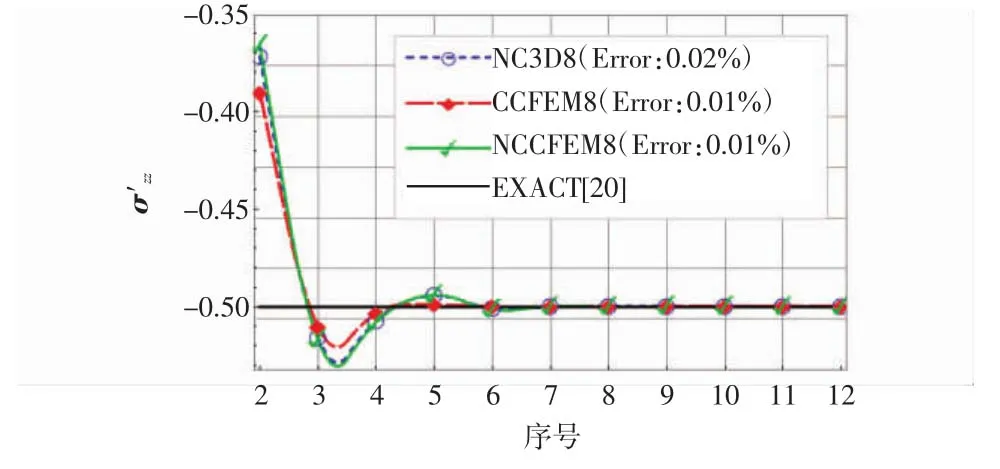
图4 σzz′与精确解比较Fig.4 Comparison between σzz′and exact solution

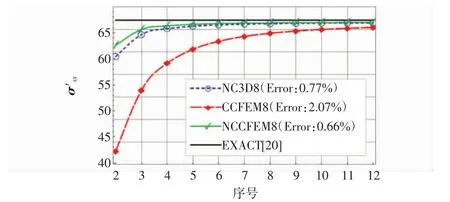
图5 σxx′与精确解比较Fig.5 Comparison between σxx′and exact solution

图 6 σxy′与精确解比较Fig.6 Comparison between σxy′and exact solution

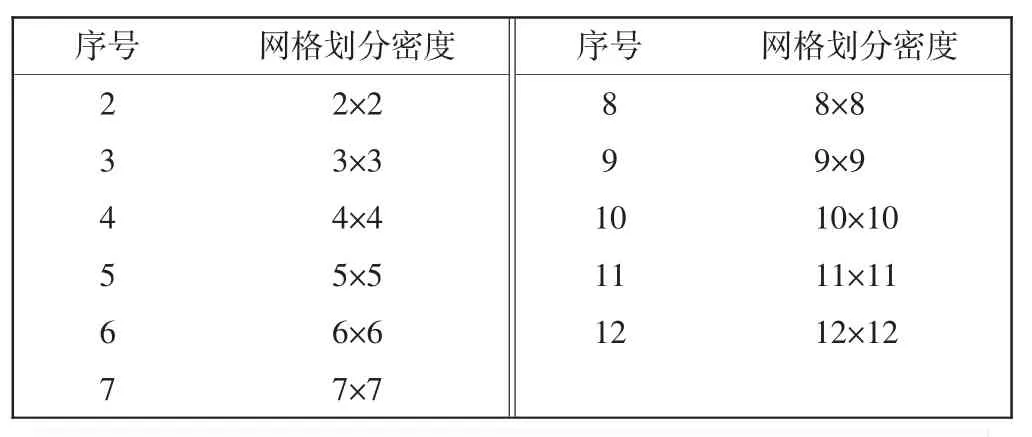
表1 网格划分的对应关系Tab.1 Corresponding relation between horizontal axis and mesh models

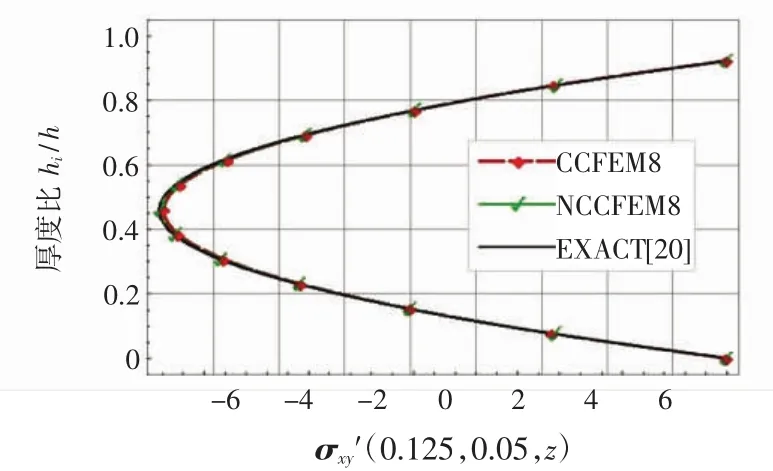
图7 σxy′沿厚度方向的分布Fig.7 Distribution of stress σxy′along thickness direction

图8 σyy′沿厚方向的分布Fig.8 Distribution of stress σyy′along thickness direction

以变量靠近最大值与最小值位置为原则，关于位移和应力的比较位置点（参见图1～图6）为

图1～图6中的误差值是在网格12×12×4模型下各单元结果与精确解的比较。从以上数据曲线图可得如下结果。

1）协调联合元 CCFEM8 的位移 u′、w′和平面内应力 σxx′、σxy′的结果不如 ABAQUS 中非协调位移元NC3D8。实质上，因为线性的协调位移元刚度矩阵的刚度大于真实材料的刚度，而引入了内部结点非协调位移项的非协调位移元的插值多项式完备，因而其刚度矩阵的刚度更真实。所以，协调位移元的应力精度是不太可能超越非协调位移元的应力精度的。但对于协调元，联合有限元方法的其他应力结果均优于NC3D8。CCFEM8元的应力结果收敛稳定性相当明显，且各变量的收敛速度比较均衡。

2）NCCFEM8的位移和应力结果均优于NC3D8的结果，且收敛速度很快，尤其是其平面外应力σxz′与NC3D8的结果比较，收敛优势明显。从上述图1～图6可看出，NCCFEM8的位移和应力结果的收敛速度和精确度基本一致；同时从图7～图8可看出，沿厚度方向各结点，应力结果的精确度也同精确解基本一致。

3）对横观材料或正交各异性材料而言，一般有限元法的平面外应力σxz′结果相对较差。实践表明，若网格进一步细分，NCCFEM8的位移和应力结果均可逼近精确解，而NC3D8的平面外应力σxz′要逼近精确解却可能需要更细的网格划分（图3）。

4）σzz′处于中性面的中间位置，3 种单元的 σzz′收敛速度快，其精度没有明显的区别（图4）。

3 结语

联合有限元方法是通过位移与外载荷关系的欧拉方程得到较精确的位移结果后，再用H-R变分原理关于应力变量变分后的欧拉方程替代本构关系求解应力。因而，避免直接用本构关系方程求解应力，提高了应力数值的精确度。

位移变量求解采用刚度矩阵对称的线性方程组求解，应力变量求解采用系数矩阵对称的线性方程组求解。对于求应力的线性方程可方便地引入应力边界条件。

从NCCFEM8的数值结果来看，其主要意义在于位移和应力的快速收敛和结果的精确性，且位移和应力的收敛速度和精确度基本一致。以有关板壳理论的H-R变分原理和势能原理为基础，同样可简便地演化出与联合有限元方法相对应的有限元方法。