基于身份的无证书双线性对密钥协商方案

顾兆军 ，刘东楠

（中国民航大学a.信息安全测评中心；b.计算机科学与技术学院，天津 300300）

通信科技的进步使信息安全的重要性逐渐凸显，会话阶段参与信息交互的双方协商一个安全可靠的密钥尤为重要。早期的密钥协商协议不仅要使用证书，还需将密钥进行托管[1]，不具备前向安全性等属性，极大程度地占据了系统资源，且证书保存及密钥托管给系统安全性带来了极大威胁。随着通信技术和无线网络的发展，需要一种新型、轻量级、安全度高的密钥协商方案，并将其应用到密钥协商协议当中，这就出现了建立在强安全性数学运算上的无证书密钥协商协议。常见的密钥协商算法有D-H算法、Shamir算法、COMSET算法等[2]，密钥协商协议主要基于某种数学难题，如DL问题、DH问题、CDH问题等，算法的设计主要结合椭圆曲线密码技术、双线性对技术等数学方法。

1976年，Diffie等[1]提出了第1个密钥协商方案。直到21世纪，Al-Riyami等[3]才提出第1个双线性对无证书两方认证密钥协商协议。Bonech等[4]提出了第1个经形式化证明的安全实用的加密机制。2006年，Gentry[5]提出了首个基于身份的加密方案。王圣宝[6]基于Gentry的身份基加密方案提出了带密钥托管及无密钥托管两种密钥协商方案，即IDAK协议（ID-based augmented key-agreement protocol），但 IDAK 协议不具备PKG前向安全性等安全属性。随后，其他研究者提出了IDAK协议的缺点并对其进行了分析与改进[7-11]，但改进协议又不具备密钥协商协议所需的全部安全属性。

为解决IDAK协议不具备PKG前向安全性以及改进的IDAK协议不满足密钥协商阶段全部安全属性的问题，结合双线性对技术，提出一种新的基于身份的无证书无托管双线性对密钥协商方案，该方案不仅能有效解决上述问题，还能实现无密钥托管。同时，为探究密钥协商在民航领域的应用（特别是机载天线和廊桥AP通过无线网络进行数据传输，即TWLU（ter minal wireless LAN unit）过程），首次将密钥协商算法置于特定民航信息系统中，探求不同密钥协商方案在民航领域的适用程度，将提出的方案在TWLU模拟系统中进行仿真，并与近年来的相关研究进行分析对比。

1 概述

1.1 双线性对

双线性对（Bilinear pairings):q是一个大素数，设G1是q阶循环加法群，G2是q阶循环乘法群，e:G1×G1→G2为双线性对中的一个映射，具有以下性质：

1）双线性（Bilinear）。若 g1，g2，h∈G1，有

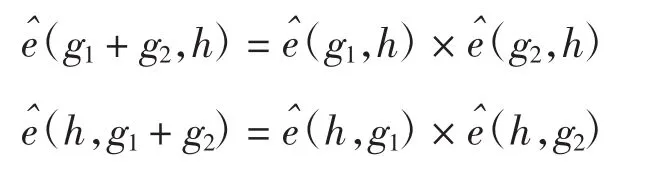
则 g，h∈G1且 a，b∈Zq，满足（ag，bh）=（g，h）ab。

2）非退化性（Non-degenerate）。若 g∈G1，则（g，g）≠1。

3）可计算性（Computability）。若 g，h∈G1，则（g，h）可计算。

1.2 数学难题

1.2.1 离散对数问题

定义1 离散对数（DL,discrete logarithm）。设G为由α生成的q阶循环群，x∈，y∈G。则满足gx=y的最小整数x，为y基于g的离散对数。

定义2 离散对数问题（DLP,discrete logarithm problem）。给定 P，Q∈G，找出 n∈，使得 P=nQ。

目前尚未找到求解DLP的多项式时间算法，解决D-H问题的关键在于求解DLP，故解决D-H问题是困难的。关于D-H问题，除了其与解决DLP难度相当，还衍生出了相关变形，如CDH问题、DDH问题、BDH问题、DBDH问题等。

1.2.2 D-H问题

定义3 计算Diffie-Hellman问题（CDH,computationalDiffie-Hellman）。设 G1为 q阶循环群，g为G1的生成元，则对于（g，ga，gb）∈G1，其中a，b∈Zq，计算gc=gab。

定义4 判定Diffie-Hellman问题（DDH，decision diffie-hellman）。设G1为q阶循环群，g为G1的生成元，则对于（g，ga，gb，gc）∈G1，其中a，b，c∈Zq，判定gc=gab是否成立。

定义5 双线性Diffie-Hellman问题（BDH,bilinear Diffie-Hellman）。设 q 阶循环群 G1，G2，g 为 G1的生成元，且：G1× G1→G2，则（g，ga，gb，gc）∈G1，其中 a，b，c∈Zq，计算（g，g）abc。

定义6 判定双线性Diffie-Hellman问题（DBDH,decision bilinear Diffie-Hellman）。设 q阶循环群 G1，G2，g 为 G1的生成元，且:G1× G1→G2，则对于（g，ga，gb，gc）∈G1和 Y∈G2，其中 a，b，c∈Zq，判定 Y=（g，g）abc是否成立。

2 基于身份的密钥协商方案

2.1 经典方案回顾

1）Diffie-Hellman密钥协商算法

在D-H算法中，参与密钥协商的双方（A和B）能够使用该算法协商出秘密密钥，算法描述如下：

Step 1 A选择一个大随机数x，发给B

X=gxmod n；

Step 2 B选择一个大随机数y，发给A

Y=gymodn；

Step 3 A计算k=Yxmod n；

Step 4 B 计算 k′=Xymod n；

∵ k=k′=gxymod n；

∴k即为A和B的秘密密钥。

2）Gentry加密方案

Gentry方案主要分为4个阶段，即系统建立（Setup）、私钥生成（KGen）、加密（Encrypt）及解密（Decrypt），描述如下。

Step 1(Setup) PKG 选择 g，h，t∈G1，g，h，t是 G1的生成元，α∈Zp，g1=gα∈G1。公共参数为，主私钥为α。

Step 2(KGen) PKG选择rID∈Zp，计算长期私钥dID=，其中hID=（ht-rID）1/（α-ID），对于不同的身份，具有特定的rID。

Step 3(Encrypt) 选取随机数s∈Zp，计算密文C=

Step 4(Decrypt) 接收者收到密文 C=（α，β，θ）后，计算 m= θ·（α，hID）βrID，得到原始消息。

2.2 基于身份的无证书双线性对密钥协商方案

在基于身份的密码体制中，不需要使用证书，从而节省大量系统资源，需由可信第三方，即私钥生成中心（PKG,private key generator）生成私钥。传统密钥协商协议使用PKG托管用户私钥，而一旦发生PKG私钥泄露，攻击者可利用窃取的私钥生成其它信息，故大部分传统密钥协商协议不具备PKG前向安全性。结合IDAK协议，使用双线性对提出一种基于身份的无证书无托管密钥协商方案。

2.2.1 参数说明

方案使用的参数如表1所示。

表1 参数说明Tab.1 Parameter explanation

2.2.2 方案描述

本方案中，密钥协商需经过3个阶段和2次交互，3个阶段分别是系统建立（Setup）、私钥生成（KGen）和密钥协商（KAgreement），描述如下。

Step 1(Setup) PKG 选择 g，h，t∈G1，g，h，t是 G1的生成元；α∈Zp；g1=gα∈G1；公共参数为；主私钥为α。

Step 2(KGen) PKG选择rID∈Zp，计算长期私钥dID=，其中hID=（ht-rID）1/（α-ID），对于不同的身份，具有特定的rID。若只有两方进行协商，令

Step 3(KAgreement) 参与密钥协商的两方分别选择一个临时私钥x，y∈Zp，计算以及

用户A计算共享密钥KAB1、KAB2，用户B计算共享密钥KBA1、KBA2，最后计算共享会话密钥，即

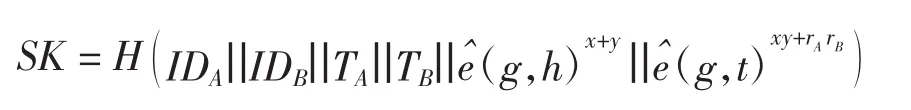
密钥协商2次交互过程如图1所示，下面使用双线性理论对该方案进行正确性证明：

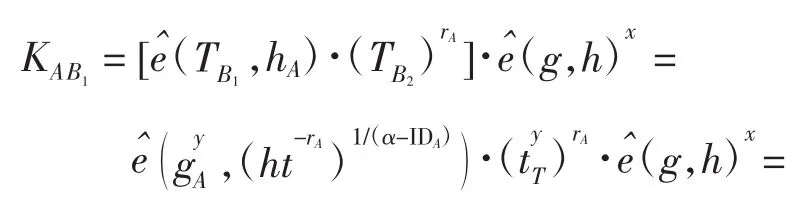
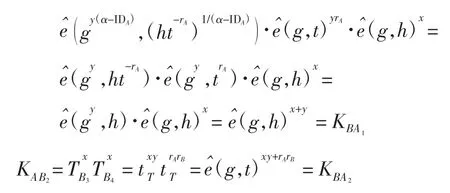
图1 提出的密钥协商过程Fig.1 Proposed key-agreement process

3 方案分析

3.1 安全属性分析

1）已知会话密钥安全（known-key security）。在该协议的每次通信中，选取不同的随机值x和y作为临时密钥，攻击者无法在使用过的密钥中找到线性关系，故本协议在随机预言模型（ROM,random oracle model）下具备已知会话密钥安全性。

2）完美前向安全性（perfect forward security）。若参与会话的某一方或两方的长期私钥或被攻击者窃取，攻击者无法通过计算得到会话密钥，因为攻击者无法通过计算得到解决本问题等同于解决 BDH问题。

3）PKG 前向安全性（forward security of PKG）。若攻击者通过某种途径得到用户主私钥α，则可通过计算得到

4）抗密钥泄露伪装攻击（key-compromise impersonation resilience）。攻击者通过某种途径窃取到A的长期私钥攻击者可伪装成A与B进行密钥协商，但无法伪装成B与A进行密钥协商，因为攻击者无法通过运算获得B的私钥，故攻击者不能得到A与B进行协商时的会话密钥。

5）抗未知密钥共享（unknownkey-share resilience）。在A和B进行密钥协商时，攻击者C试图打断该交互、强制与A或B进行协商，从而计算出会话密钥。因为在A与B的交互过程中，所传输的信息被对方公钥进行加密，C无法破解协商内容，因此C无法通过运算获得A与B进行密钥协商时的会话密钥。

6）无密钥控制（no key control）。若 A 作为“伪装者”或是攻击者，试图通过运算使协商后的会话密钥变成事先设定好的某个值，这种方法是行不通的。因为参与会话的任何一方，事先不可能知道对方的主私钥α、长期私钥dID=和临时私钥x，y。解决本问题等同于解决DBDH问题。

3.2 方案的模拟仿真

3.2.1 方案在民航领域的应用及实验环境

将第3节提出的方案应用到TWLU数据传输过程，使用无证书无托管的机制为机载无线网络传输提供方便，同时增强了密钥协商过程的安全性，为机载数据传输提供安全保障。应用背景及传输过程描述如下：飞机降落后停靠停机位时，向航空公司提交飞机健康管理数据、电子飞行包等关键数据，目前大部分机型及航空公司采用人工拷贝及GateLink（一种使用光缆及红外线进行数据传输的方式）进行数据传输。随着航电技术和无线技术的发展，Boeing等公司在新机型（如B-787）中装载了TWLU，飞机与航空公司间使用该模块和布置在廊桥上的无线接入点进行数据传输，该过程采用802.11协议。由于民航领域传输数据的特殊性，需要一种安全性更强的密钥协商机制，保证数据的安全传输。

该系统的组成有：可信的第三方私钥生成中心PKG，可由航空公司信息安全部主管；机载天线、廊桥接入点、机载数据服务器以及航空公司数据服务器。数据传输过程及网络结构如图2所示。

3.2.2 模拟仿真及效率分析

所提方案使用CPP语言实现后应用到装载上述环境的原型系统中，与近年来相关研究进行对比分析，得到以下结论。

结论1 相比其它方案，新方案满足密钥协商过程所需的全部安全属性，如表2所示。

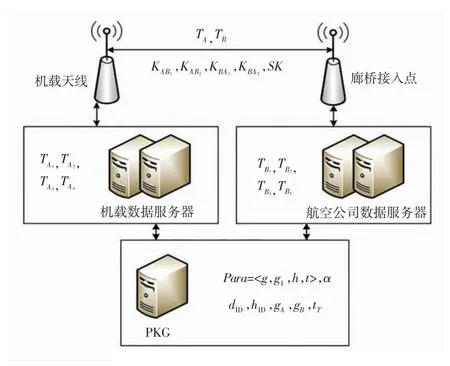
图2 方案的民航应用及实验环境Fig.2 Application in civil aviation and experimental environment

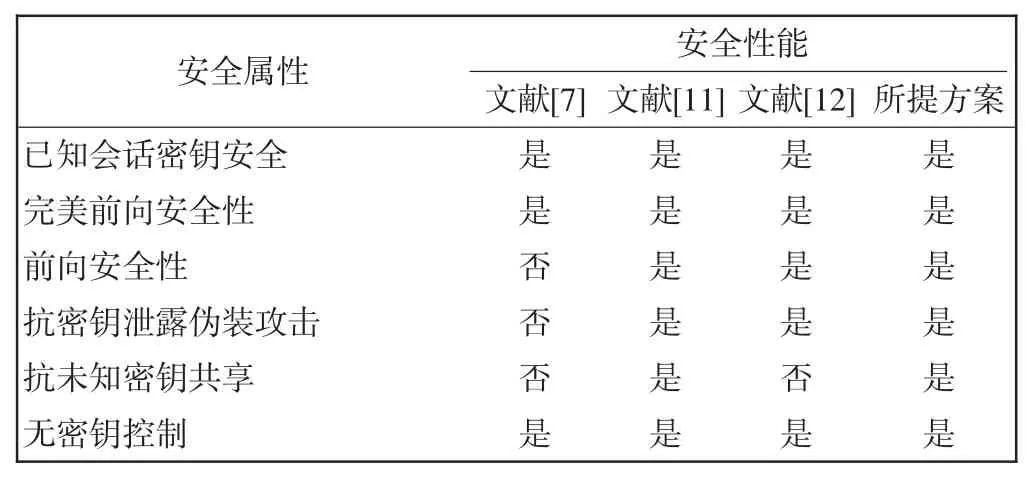
表2 安全性分析Tab.2 Security analysis

结论2 运算效率方面，设完成一次指数运算的时间为Ee，完成一次双线性运算的时间为Eb，完成一次乘法运算的时间为Em，新方案减少了双线性对运算，牺牲了指数运算（文献[11]除外），如表3所示。实验表明，一次双线性对运算所消耗的时间是正常椭圆曲线运算的20～30倍。

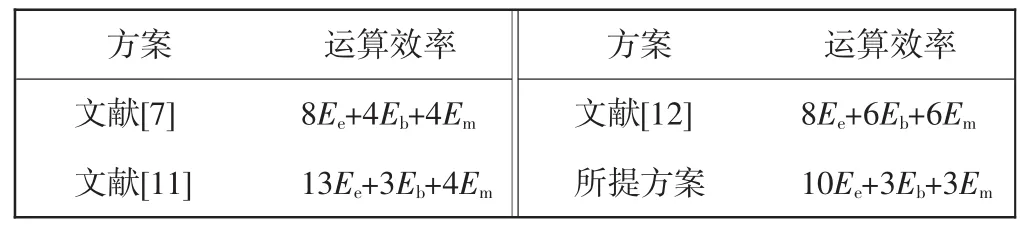
表3 效率分析Tab.3 Efficiency analysis

由表3可知，文献[11]也满足密钥协商过程中的全部安全属性，但新方案的运算效率明显高于文献[11]的方案。

综合比较文献[7，11-12]，无托管密钥SK形式如表4所示。

结论3 文献[7]的密钥方案过于简单，文献[11]和文献[12]密钥形式过于复杂，占据系统资源过多，在密钥SK中，新方案减少了指数运算和乘幂运算，并具备较高的安全性。

表4 无托管秘密密钥形式Tab.4 Form of secret key

实验表明，新方案的安全性能及最终密钥形式优于其它方案，虽增加了指数运算，但在运算性能方面减少了耗时的双线性运算。

4 结语

结合IDAK协议及近年来研究者对IDAK协议提出的改进方案，利用双线性对数学方法，提出一种新的基于身份的无证书双线性对密钥协商方案，实现了无证书无密钥托管的密钥协商，有效抵御了密钥泄漏攻击、已知/未知密钥攻击等恶意行为。将该方案置于特定民航系统中进行仿真实验，结果表明：该方案运算效率适中，与其他方案相比具有较强的安全性，更适用于民航这一特殊领域。