一种基于简化自适应SCKF的目标跟踪算法

赵 坤 徐 帆 李爱国 苗志勇 王 娜

1.北京航天自动控制研究所，北京100854 2.94402部队, 济南250002

由于机动目标的状态空间模型为非线性，因此需要采用非线性滤波算法实现目标的跟踪[1-4]。扩展卡尔曼滤波器(EKF)虽然是解决非线性估计问题的常用方法，但是EKF需要通过泰勒展开对非线性方程进行线性化处理，不但引入误差，而且Jacobian矩阵的计算也很繁琐，尤其当状态空间模型为强非线性时[5-6]。为克服EKF上述缺点，Julier S J和Uhlmann J K[7]于1997年提出无迹卡尔曼滤波器(UKF)。虽然UKF通过确定性的Sigma采样点对非线性函数的概率密度分布进行近似，有效避免了EKF的线性化过程，但是UKF没有严格的数学推导，导致其在无迹变换(Unscented Transform,UT)过程中，可能会出现负权值情况，引起滤波发散或者不稳定[8]。粒子滤波(Particle Filter, PF)虽然在精度上和稳定性上均优于UKF，但由于PF是通过随机粒子数近似非线性函数的后验密度，导致PF的计算负担过大，不利于其应用于目标的实时跟踪。此外，在PF运算过程中会出现粒子退化现象，引起PF的精度下降[9-10]。

2009年，Arasaratnam和Haykin[11]基于球面径向容积准则，经过严格的数学推导提出一种高性能非线性滤波算法—CKF(Cubature Kalman Filter)。CKF在精度上不仅高于EKF，同时由于在积分运算过程中采用等权值的容积点，因此在稳定性上要优于UKF[12-14]。但CKF在每次迭代运算过程中，都需要进行协方差矩阵的分解运算，为保证CKF在运算过程中协方差矩阵的正定性，Arasaratnam提出平方根容积卡尔曼滤波( Square-Root Cubature Kalman Filter，SRCKF)算法。但由于在目标跟踪过程中，系统噪声会受到外界干扰，造成滤波器不稳定，为进一步提高CKF在目标跟踪过程中的稳定性，同时降低运算量，本文根据跟踪目标系统的状态方程为线性的特点，提出一种简化自适应SCKF算法。该算法不需要精确知道机动目标噪声的先验统计特性，能够自适应调节目标跟踪过程中的噪声变化，有效克服外界对系统噪声干扰引起的不稳定性。 此外由于利用状态转移矩阵实现对状态变量和协方差矩阵的一步预测，有效避免了传统算法中通过容积点进行计算的复杂过程，减小了计算负担。仿真结果显示:本文提出的简化自适应SCKF在保证跟踪精度的前提下，能有效提高运算效率。

本文的结构如下：第1节介绍传统自适应SCKF算法；第2节通过对传统自适应SCKF算法时间更新环节的简化，介绍简化自适应SCKF算法；第3节通过对目标跟踪仿真验证简化自适应SCKF算法的有效性；最后给出文章的结论。

1 传统自适应SCKF算法

通常情况下，非线性系统可以表示为[9,11]：

xk=f(xk-1)+vk-1

(1)

zk=h(xk)+wk

(2)

其中，xk∈Rn表示k时刻的状态量；vk-1表示零均值过程噪声，其方差矩阵为Qk-1；wk表示零均值量测噪声，其方差矩阵为Rk；zk∈Rm表示k时刻的量测量；f(·)和h(·)分别为状态方程和量测方程的非线性函数。

在众多自适应算法中，基于Sage-Husa噪声估计器的自适应算法应用最为广泛[15]。为了更好地利用当前信息实现对系统噪声的估计，通常采用带渐消记忆的Sage-Husa噪声估计器实现对过程噪声方差矩阵Qk和量测噪声方差矩阵Rk的有效估计，此时Qk和Rk可分别表示为：

(3)

(4)

将式(3)和(4)表示的Qk和Rk，代入到SCKF中可以得到由式(1)和(2)所示非线性系统的自适应SCKF算法，具体过程可以总结如下：

第1步：根据Spherical-Radial准则计算Cubature点ξi及相应的权值ωi：

(5)

其中，[1]i为：

(6)

第2步：一步预测

计算m个Cubature点：

(7)

将Cubature点利用式(1)中的状态方程进行传播：

(8)

状态x在k时刻的预测：

(9)

过程噪声方差矩阵Qk的自适应调节

(10)

其中，dk=(1-b)/(1-bk),(0.95≤b≤0.995)。

(11)

第3步：量测更新

计算m个Cubature点：

(12)

将Cubature点利用式(2)中的量测方程进行传播：

(13)

量测z的估计：

(14)

量测噪声方差矩阵Rk的自适应调节：

(15)

自相关协方差阵Pzz的平方根为：

(16)

互相关协方差阵Pxz为：

(17)

卡尔曼增益Kk为：

(18)

更新状态量为：

(19)

更新状态误差协方差平方根：

(20)

至此，带渐消记忆的自适应SCKF算法的基本步骤介绍完毕。

2 简化自适应SCKF算法

由于在目标跟踪领域，被跟踪系统的状态方程是线性的，即式(1)改写为：

xk=Φkxk-1+vk-1

(21)

此时式(9)可以表示为[16]：

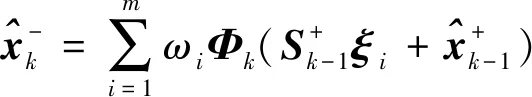
(22)

(23)

对于式(11)，由QR分解理论可以得到：

(24)

其中，H为Hermite矩阵，且HTH=I。则对式(24)进行如下运算：

(25)

式(25)左边可以表示为：

(26)

(27)

根据式(23)和(27)所示的状态变量和协方差矩阵的一步预测可知，简化自适应SCKF算法的基本流程可以表示为如图1所示。

3 简化自适应SCKF算法跟踪性能评价

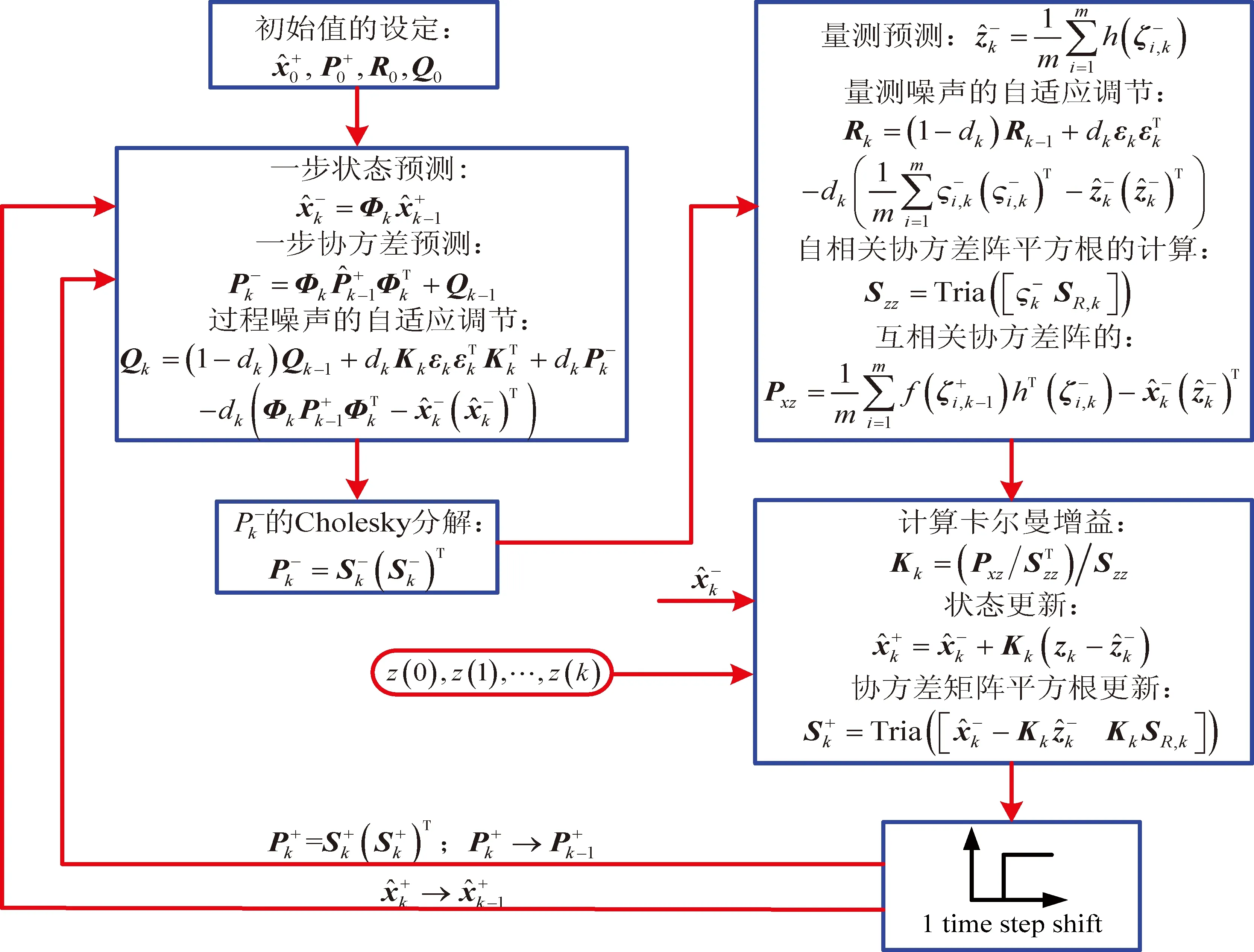
图1 自适应SCKF算法基本流程图

由于在目标跟踪过程中，量测噪声更容易受到外界环境的干扰，因此本部分在研究过程中保持过程噪声不变，同时为了全面评价简化自适应SCKF算法的性能，进行量测噪声不变和量测噪声时变2种场景的仿真分析，在每一种分析中均以传统自适应SCKF作为对比。本部分选用常用雷达目标跟踪模型，该模型的动态方程可以表示为[8,17]：

(28)

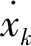
(29)

其中,q1=0.1；T=1s。

量测方程可以表示为：

(30)

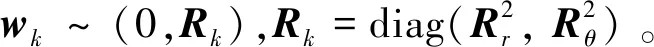
Rk=diag[100m210mrad2],1≤k≤100

(31)

(32)

状态向量的初始值设为[1000m 300m/s 1000m 0m/s]T；初始协方差矩阵设为：

评价一种滤波算法的好坏主要从精度和运算效率2个方面进行。在精度方面主要采用均方根误差(Root Mean Square Error,RMSE)作为评价因子；在运算效率方面主要从多次蒙特卡罗运算耗费的时间进行评价。上述被跟踪目标的位置、速度和转弯速率的RMSE可以分别表示为：

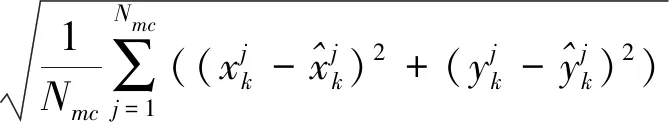
(33)

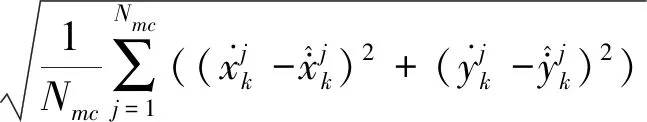
(34)

式(31)和 (32)所示的场景1和场景2 在配置内存为3GB，频率为2GHz，Intel双核处理器计算机中进行50次蒙特卡罗仿真，结果分别如图2和3所示，2种场景的RMSE因子的统计特性和所耗费的时间统计如表1所示。

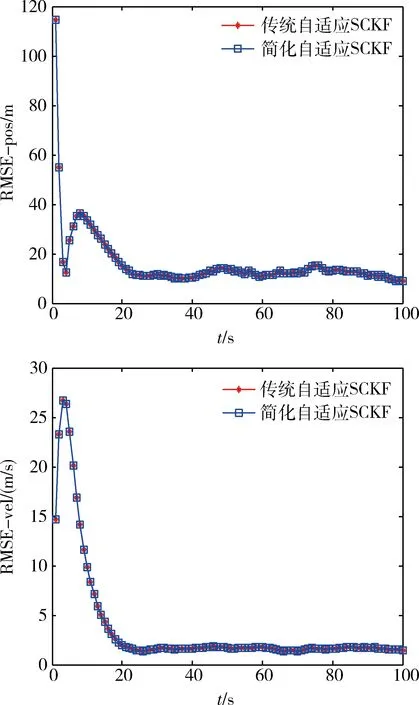
图2 场景1的仿真结果

由图2可知，在场景1中，传统自适应SCKF和简化自适应SCKF在量测噪声不变的情况下，位置的均方根误差和速度的均方根误差的收敛趋势均保持一致，这说明自适应SCKF同样适用于量测噪声不变的情况。由表2的统计特性可知，简化自适应SCKF在保证跟踪精度的前提下，有效降低了计算负担。

图3 场景2的仿真结果

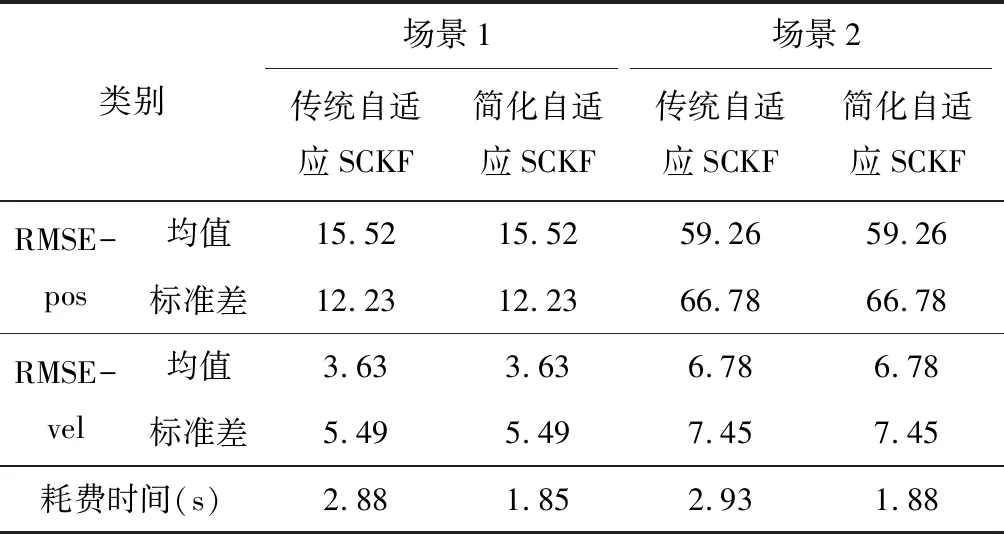
表1 场景1和场景2仿真结果统计特性

如图3所示，传统自适应SCKF和简化自适应SCKF在场景2中可以有效调节量测噪声对系统造成的影响，最终实现收敛。由表2中的统计特性可知，传统自适应SCKF和简化自适应SCKF在场景2中的跟踪精度相同，但是相比于传统自适应SCKF，简化自适应SCKF有效提高了运算效率。综上所述，本文提出的简化自适应SCKF不但能保证与传统自适应SCKF算法同样的跟踪精度，而且可以有效提高实时性。

4 结论

基于目标跟踪系统的状态方程通常为线性的，提出一种简化自适应SCKF算法，该算法直接利用状态转移矩阵代替容积点，实现对状态变量和协方差矩阵的一步预测。为有效评价该简化自适应SCKF算法的有效性，将其与传统自适应SCKF算法在量测噪声不变和量测噪声时变两种目标跟踪场景下进行仿真对比分析，结果显示：本文提出的简化自适应SCKF算法具有与传统自适应SCKF算法同样的跟踪精度，但其计算负担小于传统自适应SCKF。