基于时空域三维约束的多帧图像超分辨算法

黎海雪，林海涛，姚晓诚



基于时空域三维约束的多帧图像超分辨算法

黎海雪1，林海涛1，姚晓诚2

（1. 海军工程大学电子工程学院，武汉 430033；2. 河北省国控投资管理有限公司综合办公室，河北石家庄 050000）

对基于时空域三维正则约束的多帧图像超分辨算法进行了研究，首先在基于马尔科夫随机场的自适应正则约束的基础上，进一步引入多帧图像间的时域约束，建立了时空域三维正则约束模型，并提出了相应的超分辨方法；之后通过仿真实验对本文方法进行了仿真测试，结果表明本文方法能够取得更好的超分辨效果。

时空域 三维约束 多帧图像 超分辨算法

0 引言

单帧图像超分辨只依赖于单帧低分辨率图像对高分辨率图像进行重建，可用信息量少，重建问题的不适定性较强，因而重建结果经常出现模糊效应、振铃效应等，影响超分辨结果的视觉效果。随着相机工艺的不断提升，特别是智能手机等消费级相机的普及，人们可以随时随地随手进行拍摄。随着相机CCD阵列信噪比的不断提升，曝光时间大大缩短，使得高帧频连续拍摄成为可能。为此人们希望通过连续拍摄的多帧低分辨率图像重建得到原始场景的高分辨率图像，即多帧图像超分辨。

多帧图像超分辨问题中的多帧低分辨率输入图像一般视为同一成像条件下、同一设备对同一场景在短时间内的连续成像，由于智能手机等手持设备在连续拍摄过程中由于手部抖动等因素，造成多帧低分辨率连续成像之间存在细微的位移，如何处理多帧低分辨率图像间的位移关系，实现多帧低分辨率图像信息的有效融合，是多帧图像超分辨的关键。传统方法主要依赖于图像配准提供多帧低分辨率图像间的位移关系，但光流法[1]等图像配准方法计算量较大，同时先配准后融合的超分辨方法造成了两个环节的割裂，配准误差容易造成图像融合后产生振铃等效应；为了实现自适应的多帧低分辨率图像融合，文献[2]中提出的基于马尔科夫随机场模型的自适应正则约束进一步推广到多帧图像超分辨问题中，实现了多帧低分辨率图像的自适应融合与超分辨。

1 基于时空域三维约束的多帧图像超分辨算法

对于多帧图像超分辨来说，多帧低分辨率图像虽然提供了信息增量，与单帧图像超分辨问题相比有一定程度的适定化，但如何实现多帧低分辨率图像的融合成为影响多帧图像超分辨性能的关键。传统的多帧图像超分辨多采用两段式的处理方式，即先对多帧低分辨率图像进行图像配准，之后对高分辨图像进行迭代重建，而重建过程中的正则项只考虑单帧图像中的空域信息，多帧图像间的时域信息没有得到较好的利用。针对这一问题，本节利用马尔科夫随机场模型描述多帧图像中时空域局部邻域特性，并据此建立时空域三维自适应约束，从而在空域自适应正则化的基础上，进一步充分利用了多帧图像间的时域信息，提高了正则项的准确性，提高了多帧图像超分辨的性能。

2 时空域马尔科夫随机场模型

2.1 先验概率模型

令图像标记层的标记值表示图像像元的局部突变特性，即像元为边缘的可能性，为此定义N分类的图像标记值取值集合为：

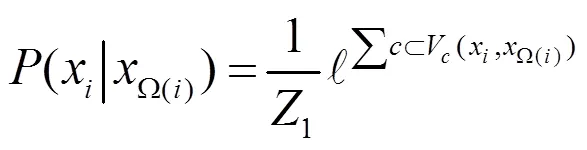
为了提高先验概率模型对图像的自适应描述能力，设计了单位置势函数与双位置势函数两种不同类型的势函数。其中单位置势函数主要以抑制图像中的高频信息为主；双位置势函数主要考虑到图像三维局部邻域空间内的一致性。得到单位置势函数与双位置势函数：

图1 三维邻域空间示意图

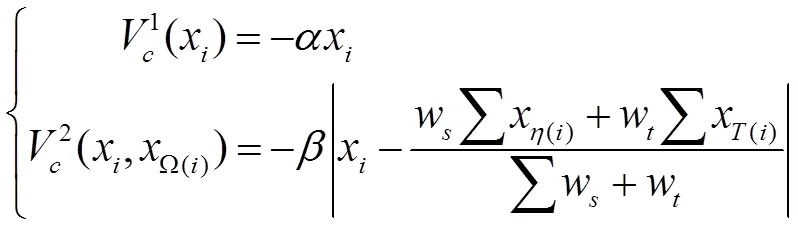
2.2 条件似然概率模型

先验概率模型建立了三维局部邻域空间内标记值间的概率关系，参考经典的马尔科夫随机场模型，得到时空域三维空间下的条件似然概率模型为：

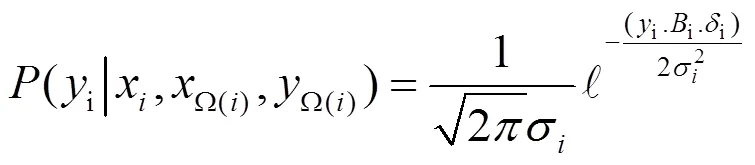
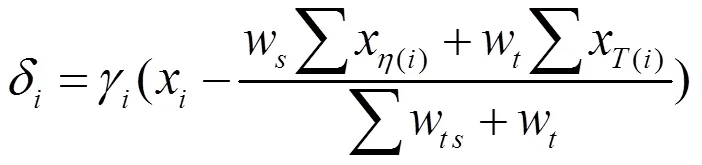
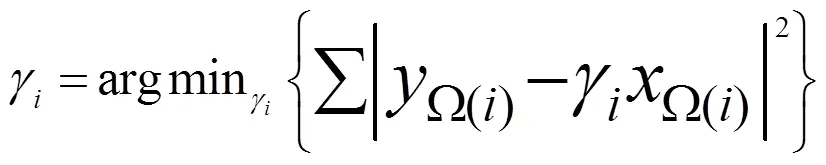
作为一个典型的二次型问题，可以解得

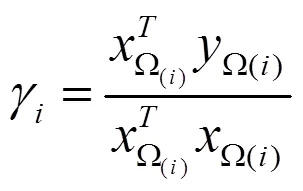
2.3 生成的马尔科夫随机场模型

得到先验概率模型与条件似然概率模型后，即可得到最终的马尔科夫随机场模型为

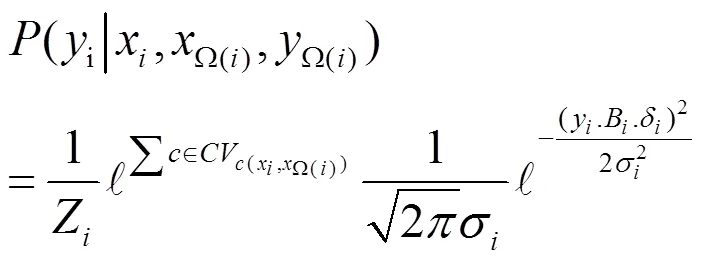
时空域三维马尔科夫随机场模型作为生成的马尔科夫随机场模型，同样需要通过迭代最大化马尔科夫随机场模型的概率值得到最终的图像标记值，因此同样需要设置收敛条件判断迭代是否需要停止。

3 基于时空域马尔科夫随机场模型的三维正则约束

参考文献[2]基于马尔科夫随机场模型的自适应正则约束，将其进一步推广至时空域三维空间，得到自适应正则约束项为：

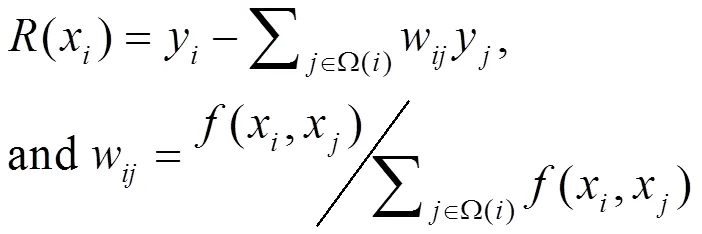
4 基于时空域三维约束的多帧图像超分辨算法

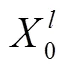
输出：多帧图像超分辨重建结果

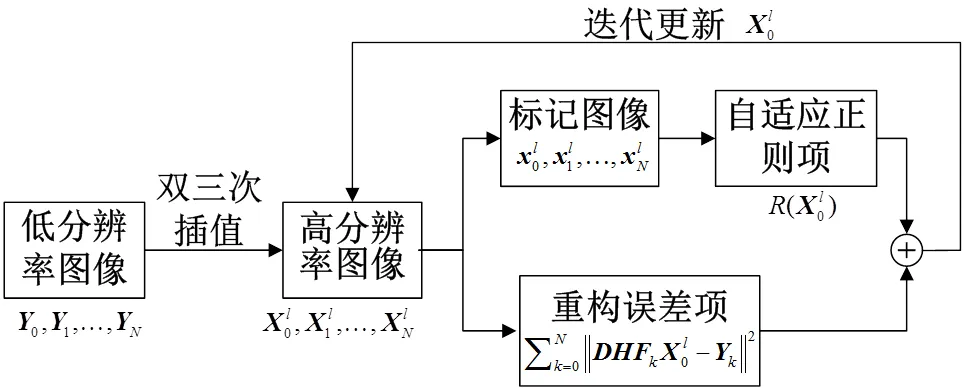
图2 算法流程图

5 仿真分析

为了验证本文提出的基于时空域三维自适应约束的多帧图像超分辨算法性能的有效性，本节对所提算法进行了大量的仿真实验。首先，利用本文所提算法与典型多帧图像超分辨算法进行了对比试验；最后对本文所提算法的鲁棒性进行了分析。在对比实验中，本节选择了经典的Tikhonov正则化多帧图像超分辨方法[3]、TV正则化多帧图像超分辨方法[4]、BTV正则化多帧图像超分辨方法[5,6]作为典型的多帧图像超分辨方法。

本节利用Set5与Set14中的原始图像作为高分辨率图像，随机生成-1个二维偏移向量(△,△)，其中△表示方向的偏移量，且△∈(-1，1)，△表示y方向的偏移量，且△∈(-1，1)这里只考虑帧间偏移量为亚像元情况，对于偏移量超过1的情况，可以先配准转换为亚像元。之后利用Matlab自带的imresize()函数在bicubic模式下对帧高分辨率图像进行缩放，得到不同缩放因子下的低分辨率图像，并将低分辨率图像作为输入，对比不同算法的超分辨性能。参照其他论文中仿真设置，本节同样只在Y通道对图像进行超分辨操作，对于CbCr通道只利用bicubic上采样进行插值放大，最后将得到YcbCr通道重新转换回RGB通道得到最终超分辨结果。

5.1 超分辨性能对比分析

多帧图像超分辨中使用低分辨率图像的帧数，空域邻域系统权重s，时域邻域系统权重w，参考其他论文中参数，=10，s=1，w=1，超分辨性能达到最佳。利用Tikhonov正则化、TV正则化多、BTV正则化作为多帧图像超分辨对比方法，在Set5与Set14两个数据集上对不同缩放因子进行了对比试验，得到不同情况下各超分辨方法的PSNR与SSIM如表1所示。

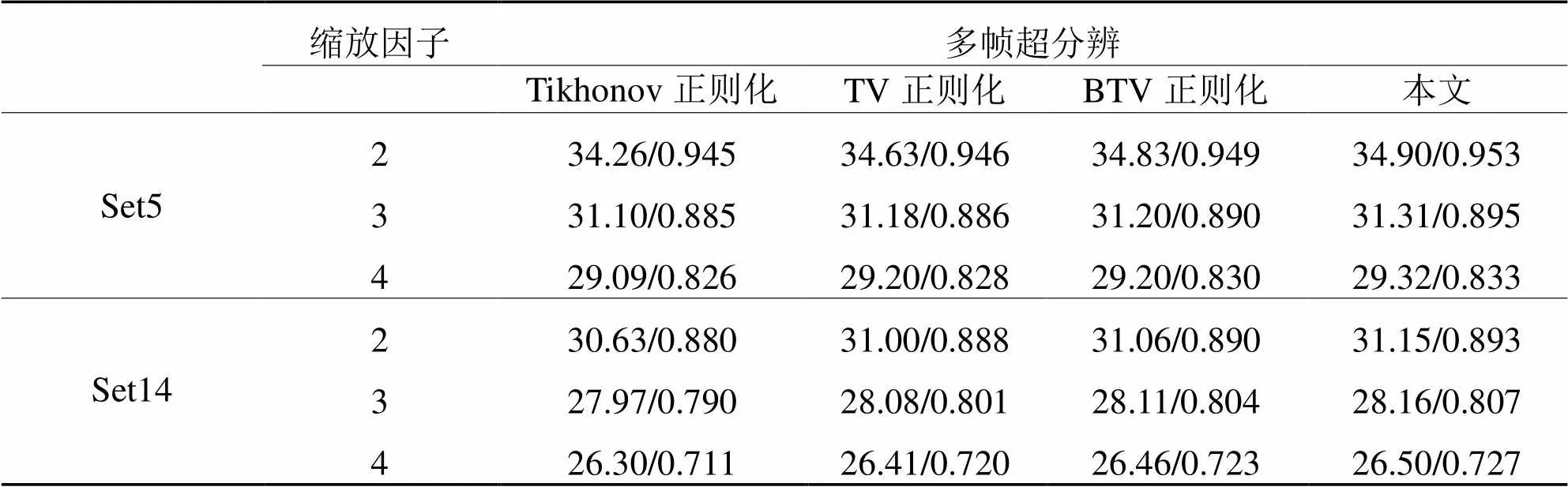
表1 不同方法超分辨性能对比

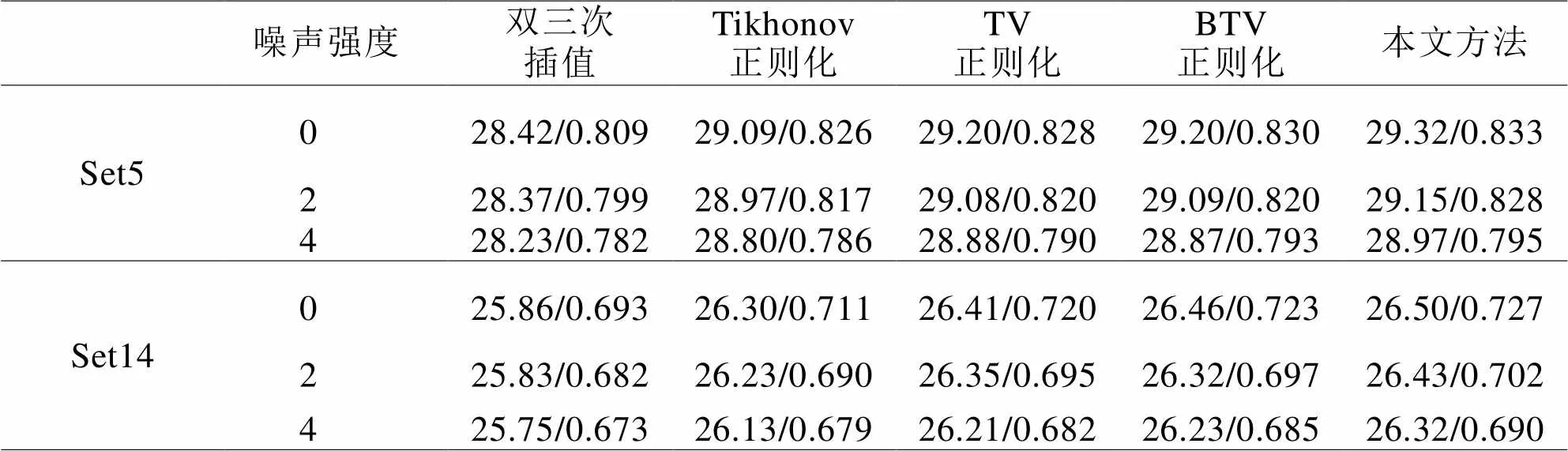
表2 不同噪声强度下不同方法超分辨性能对比

通过表1可以看出，本文提出的多帧图像超分辨方法的超分辨性能较其他多帧超分辨算法优势有明显提高。进一步对比同缩放因子下多帧图像超分辨算法的性能可以看出，本文所提方法在Set5与Set14两个数据集上均取得了较好的超分辨效果当缩放因子为2时，在Set5数据集上，本文所提方法的PSNR/SSIM值与Tikhonov正则化方法、TV正则化方法以及BTV正则化方法相比，分别提高了0.64，0.27，0.07dB；当缩放因子进一步提高到3、4时，本文所提方法仍然具有性能优势。

当缩放因子为4时，在Set5与Set14两个数据集上，统计得到本文所提算法与多帧图像超分辨对比算法的PSNR与运行时间对照图3所示。

通过图3可以看出，本文所提方法由于在超分辨过程中需要同步对马尔科夫随机场模型进行迭代，每次迭代的计算量高于TV正则方法、BTV正则方法，因此运行时间略长，但本文所提方法取得了最优的超分辨性能。整体来看，本文所提多帧图像超分辨方法在保证较高的运行效率基础上，取得了较好的超分辨效果，在实际应用中具有较高的应用价值。

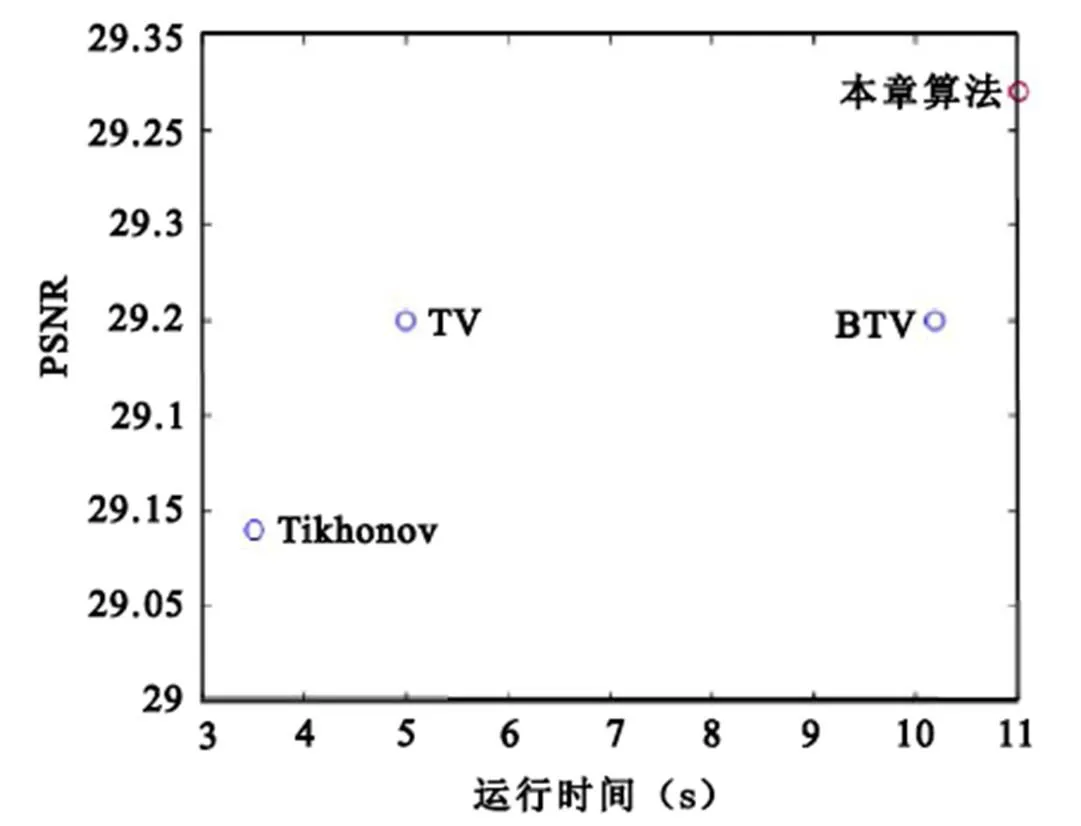
图3 不同方法超分辨性能与运行时间关系图

5.2 鲁棒性分析

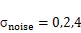
进一步通过上表可以看出，本文所提算法与其他对比算法相比，在不同噪声强度下的PSNR/SSIM值均达到最优。当噪声强度为2时，在Set5数据集上，本文所提方法的PSNR/SSIM值与双三次插值方法、Tikhonov正则化方法、TV正则化方法以及BTV正则化方法相比，分别提高了0.78，0.18，0.07，0.06 dB；当噪声强度进一步提高到4时，本文所提方法仍然具有性能优势。

6 总结

本文主要对多帧图像超分辨问题进行了研究。传统的多帧图像超分辨方法主要通过图像配准后的图像融合实现超分辨，但这种两段式的处理流程容易在图像配准环节引入误差，影响图像超分辨性能，同时传统的正则化方法难以充分利用多帧图像中的时空域信息，容易产生模糊、振铃等效应，影响超分辨的视觉效果。

[1] Strecha C, Gool L V, Fransens R. Optical flow b-ased super-resolution: A probabilistic approach[J]. Computer Vision & Image Understanding, 2007, 106(1): 106-115.

[2] 秦龙龙, 钱渊, 张晓燕等. 基于自适应约束正则HL-MRF先验模型的MAP超分辨率重建[J]. 计算机应用, 2015, 35(2): 506-509.

[3] X. Zhang, E.Y. Lam, E.X. Wu, K.K. Wong. Appl-ication of Tikhonov regularization to super-resolut-ion reconstruction of brain MRI image[J]. LectureNotes in Computer Science, 2008, 4987: 51-56.

[4] M. K. Ng, H. Shen, E. Y. Lam, L. Zhang. A total variation regularization based super-resolution reconstruction algorithm for digital video [J]. EURASIP Journal on advances in signal processing, 2007, 74585: 1-16.

[5] S. Farsiu, M. D. Robinson, M. Elad, P. Milanfar. Fast and robust multi-frame superresolution [J]. IEEE Transactions on Image Processing, 2004, 13(10): 1327-1344.

[6] 路陆, 金伟其, 王霞等. 基于低分辨率图像约束的BTV图像去模糊算法[J]. 北京理工大学学报, 2017, 37(6): 644-649.

Multi-frame Image Super-resolution Algorithm Based on Space-time Three-dimensional Constraints

Li Haixue1, Lin Haitao1, Yao Xiaocheng2

（1. School of Electronic Engineering, Naval University of Engineering, Wuhan 430033, China；2. Integrated Office of Hebei Province State Control Investment Management, Shijiazhuang 050000, Hebei, China）

TM391.41

A

1003-4862（2019）03-0057-05

2018-08-10

黎海雪（1983-），男，助理工程师。研究方向：通信与信息系统技术及应用。E-mail: 1365548@qq.com。