基于PCA-AHPSO-SVR的煤层瓦斯含量预测研究*

魏国营，裴 蒙

(1.河南理工大学 安全科学与工程学院，河南 焦作 454000;2.河南省瓦斯地质与瓦斯治理重点实验室—省部共建国家重点实验室培育基地，河南 焦作 454003)

0 引言

煤炭是我国的主体能源，占我国一次能源消费的六成以上。与此同时，煤炭事故灾害种类多且较为严重，瓦斯、水害、火灾、冲击地压等灾害一应俱全[1]，其中瓦斯事故占煤矿事故的比例较高。据统计，2006到2016年，瓦斯事故共发生1 462次，占事故总数的10.38%，死亡人数6 364人，占总死亡人数的27.31%，平均单次死亡率为4.35之多[2]。

煤层瓦斯含量是预测矿井瓦斯涌出量和煤与瓦斯突出、进行瓦斯抽放防治的重要依据之一[3-5]，准确地预测煤层瓦斯含量对煤矿瓦斯事故的防治具有重要指导意义。但煤层瓦斯含量影响因素众多，瓦斯赋存具有复杂性、非线性、动态性和随机不确定性等特性[6]，使得准确预测煤层瓦斯含量面临困难。近年来，国内外研究人员提出了许多方法来解决这一问题，如多元回归[7]、灰色理论[8]、人工神经网络[8-11]、支持向量机(Support Vector Regression，SVR)[10-12]等。其中，人工神经网络和SVR效果较好，但人工神经网络追求结构风险最小化的思路，容易出现过学习现象；而基于统计学理论的SVR，以结构风险最小化为原则，弥补了人工神经网络的不足，且具有良好的泛化能力[12]。魏建平等[9]将煤与瓦斯突出危险性预测中断层、褶皱、煤岩层倾角的定量评价方法应用到煤层瓦斯含量的BP神经网络预测模型中，取得了较好的效果；刘程程等[11]将主成分分析法(Principal Component Analysis，PCA)应用于支持向量回归机煤层瓦斯含量预测，消除影响因素之间的相关性，降低数据的维度，提高了预测的准确率；姜谙男等[12]将标准粒子群算法(Particle Swarm Optimization，PSO)用于优化支持向量机参数，避免了参数选择的盲目性。

虽然SVR对比神经网络有一定的优势，但是预测精度受参数选择影响较大。而PSO在对SVR参数寻优时存在稳定性不强的现象，并不能很好的解决SVR的参数选取问题。同时针对SVR在煤层瓦斯含量预测方面没有考虑地质构造影响的情况。本文在前人研究的基础上，综合考虑影响瓦斯赋存的多种因素，采用PCA降维，将改进的自适应混合粒子群算法(Adaptive Hybrid Particle Swarm Optimization，AHPSO)用于SVR进行参数寻优，建立回归模型。

1 PCA-AHPSO-SVR基本原理

PCA[13]是通过构建原始变量的适当线性组合来获得一系列线性无关的综合变量，从中选取若干个综合变量使其含有足够多的原始变量信息。

SVR的本质是通过核函数将低维非线性数据映射到高维空间，使其呈现线性，从而进行线性回归，以上问题可以转化为凸二次规划问题。

PSO的优点在于简单、容易实现并且调整参数不多，但在复杂函数的多峰极值问题中很容易陷入局部最优，发生早熟收敛情况，难以得到满意的最优解。这是因为标准粒子群中惯性权重w为固定值，较大的w会使粒子下一步产生较大的速度而错过最优点，较小的w会使粒子下一步产生较小的速度陷入局部最优[14]。为了避免算法早熟收敛及后期粒子在最优解附近徘徊震荡的现象，文献[15]引入1种自适应粒子群算法，如式(1)所示:

(1)

式中：wmax，wmin分别为粒子惯性权重的最大值和最小值；f为当前粒子的适应度值；favg为每代粒子的适应度值的平均值；fmin为粒子群中的最小适应度值。

该算法可以根据粒子的当前适应度值调整惯性权重，对大于平均适应度值的粒子取较小的w，使其得到保护；对小于平均适应度值的粒子取较大的w，使其更快趋向于更好地搜索空间。同时，当粒子趋于局部最优时，w增加，当粒子分散时，w减少。该算法有效地平衡了搜索和开发的能力，确保了粒子的多样性和收敛性。

为了进一步提升算法的认知能力，防止算法陷入局部最优，产生早熟现象，在自适应粒子群算法中添加位置变异算子，即选择一定比例的粒子，重新对其位置的某一维度在设定范围内随机分布。各个粒子的自适应粒子位置变异算子计算公式为：

(2)

式中：xmax,d,xmin,d为粒子的取值范围；δ为变异因子；CR为阈值。

2 PCA-AHPSO-SVR模型及评估方法

2.1 PCA-AHPSO-SVR模型

SVR的参数选取对模型结果有很大影响，在训练集相同的情况下，不同参数的选取对回归预测的结果有很大差异。本文中PCA-AHPSO-SVR模型在利用PCA消除相关变量、减少数据维度的同时，综合了AHPSO算法高效的全局搜索能力与SVR良好的泛化能力，可以有效地应用于煤层瓦斯含量预测。

PCA-AHPSO-SVR模型中采用的径向基核函数 ( Radial Basis Function，RBF) 的参数宽度g，SVR中的惩罚系数C和不敏感损失函数参数ε对建模的预测精度和泛化能力均有影响。将这3个参数分别作为自适应粒子群中粒子速度、位置和方向的3个维度，以均方根误差函数作为其对应的适应度函数，不同位置的粒子(即不同的参数组合)会反馈回来不同的适应度值，用以判断粒子位置(参数组合)的好坏。计算流程如图1所示，具体实施步骤如下：

1)读取样本数据，对数据进行预处理(归一化及PCA降维)，并产生训练集、测试集。

2)程序初始化。初始化粒子速度与位置，将SVR的3个参数(C，g，ε)作为每个粒子的三维坐标。

3)粒子适应度值计算及比较，以设定的适应度函数即均方差函数为评定函数，计算各粒子的适应度值并比较，确定群体最优适应度值。

4)更新粒子速度及位置。

5)终止条件判断。达到最大迭代次数或适应度小于给定精度时，输出最优组合参数C，g，ε，否则继续迭代。

6)根据输出最优参数，建立支持向量回归机模型，对测试集进行预测和反归一化，得到预测结果。

图1 具体计算流程Fig.1 The specific calculation flow chart

2.2 预测精度评估方法

为了评估所建立预测模型的精确度和稳定性，采用以下参数对瓦斯含量预测结果进行评估：

1)平均绝对误差MAE，反映预测值偏离真实值的大小。

2)平均相对误差MRE，反映预测值的可靠性。

3)均方根误差RMSE，反映预测值与真实值之间的离散程度。

4)预测模型的精准度FMA。

以上几个参数的计算公式如下：

(3)

(4)

(5)

(6)

式中：n为样本数；i=1,2，…，n；Xi为真实值；Xi′为预测值。

3 现场应用

3.1 影响因素的选取

根据煤层瓦斯含量的现有研究情况[8-16]，确定影响煤层瓦斯赋存的主要地质参数包括煤深、上覆基岩厚度、围岩等效系数[10]、煤厚、褶皱复杂系数、断层复杂系数和煤岩层倾角系数[17]。

煤层瓦斯含量预测训练样本用X表示，样本为：

(7)

式中：Khl为瓦斯含量，m3/t；Kms为埋深，m；Kjy为上覆基岩厚度，m；Kwy为围岩等效系数；Kmh为煤厚，m；Kzz为褶皱复杂系数；Kdc为断层复杂系数；Kqj为煤岩层倾角复杂系数。

断层复杂程度系数Kdc反映了统计单元内断层对整个单元的破坏程度，其计算公式如下：

(8)

式中：S为统计单元面积，m2；H为断距，m；L为统计单元内断层的延伸长度，m；α为断层倾角，(°)。

褶皱复杂程度系数计算公式为：

(9)

式中：Lmax为计算单元内弯曲度最大的等高线的长度，m；Lmaxo为计算单元内弯曲度最大的等高线两端点间的最短距离，m。

倾角复杂程度系数的计算公式为：

(10)

式中：αmax为统计单元内煤层最大倾角，(°)；αmin为统计单元内煤层最小倾角，(°)。

以九里山矿煤样为例，提取出30组样本数据，如表1所示。

3.2 样本数据的预处理

将表1中前20组数据作为训练样本，后10组数据作为测试样本。首先对样本数据归一化，归一化函数采用MATLAB中的mapminmax函数，归一化区间为[-1,1],将归一化后的数据进行PCA降维处理，结果如图2所示。为了尽可能多地保留原数据所持有的信息，选取90%以上的累积贡献率，即选取前5个主成分作为模型的输入。

样本序号瓦斯含量/(m3·t-1)埋深/m基岩厚度/m煤厚/m围岩等效系数断层系数褶皱系数倾角系数131.01305.42207.995.390.339 40.173 80.000 20.040 3225.63327.96191.745.740.450 80.306 20.000 10.035 4327.63530.00334.4110.590.410 50.042 10.000 40.042 1415.72485.78281.146.640.538 10.097 70.000 10.029 059.67284.00144.485.620.300 00.033 80.001 20.016 6612.53400.92256.233.610.774 00.026 40.004 80.019 3716.71400.92256.233.610.774 00.026 40.004 80.027 8812.74400.92256.233.610.774 00.000 90.000 10.031 5927.86309.48174.285.800.315 80.148 00.000 80.030 21013.38474.73306.272.660.371 80.001 50.000 50.022 21125.32350.41209.546.080.900 00.141 60.181 20.019 11213.36334.80206.453.060.356 30.000 60.019 60.053 81326.43449.32265.313.250.900 00.198 40.011 90.023 5146.99286.04163.382.160.512 50.007 50.002 30.024 81511.14350.35234.836.520.367 60.002 50.000 10.024 61612.62379.35245.306.850.810 00.001 50.000 20.021 41717.01407.12254.096.440.418 50.000 80.000 50.019 81811.28303.55177.697.930.431 70.393 50.001 60.022 71922.19283.03157.777.410.300 00.033 20.000 60.029 0209.13284.00144.485.620.300 00.033 80.001 40.023 52115.27438.26241.674.840.400 00.001 60.000 10.021 32217.72500.97308.555.350.300 00.006 40.000 10.014 82318.99363.62219.255.790.566 30.100 30.000 40.044 02417.20324.24192.015.500.484 80.292 40.000 80.014 22511.20295.22157.956.570.300 00.000 50.000 90.021 12616.96176.4472.108.130.390 30.000 50.000 50.021 22720.83274.15165.953.180.352 40.209 70.006 90.027 82810.29332.63201.185.430.300 00.000 90.089 30.019 32917.12156.8252.847.790.423 10.103 80.000 30.022 63015.65221.50107.586.680.669 80.000 80.000 60.016 6

3.3 模型参数的设置

把预处理后的样本数据作为模型的输入，基于MATLAB平台编写程序，详细流程如图1，设定APSO参数如下：粒子规模设置为40，迭代次数设置为300次，加速常数C1，C2设置值为1.494 45，惯性权重w根据适应度值更新，将ε-SVR的3个参数作为粒子群速度和方向的3个维度，参数C，g的寻优边界设置为[2-10，210]，ε的寻优边界设置为 [10-4，1]。

3.4 模型训练与预测结果分析

为了验证PCA-AHPSO-SVR模型对煤层瓦斯含量的预测性能，选用PSO-SVR模型和PCA-PSO-SVR模型进行比较，3个模型均采用RBF核函数，PSO算法和AHPSO算法设置相同的参数。由于PSO算法和AHPSO算法都是启发式算法，因此具有一定的随机性，单次运行结果并不能很好地表明三者的区别，因此在相同的运行环境下，分别将3种模型运行30次。首先对各模型的最优解和实测值进行比较，并计算最优解和预测集中各样本的相对误差以验证预测精准性，其中PCA-AHPSO-SVR的最优解的寻优结果为C=145.973 6；g=1.009 5，ε=0.088 3，结果如表2所示；然后对30次运行结果基于所构建的评估方法进行评估，选取最优解、最差解和平均解来验证3种模型的性能，结果如表3所示。

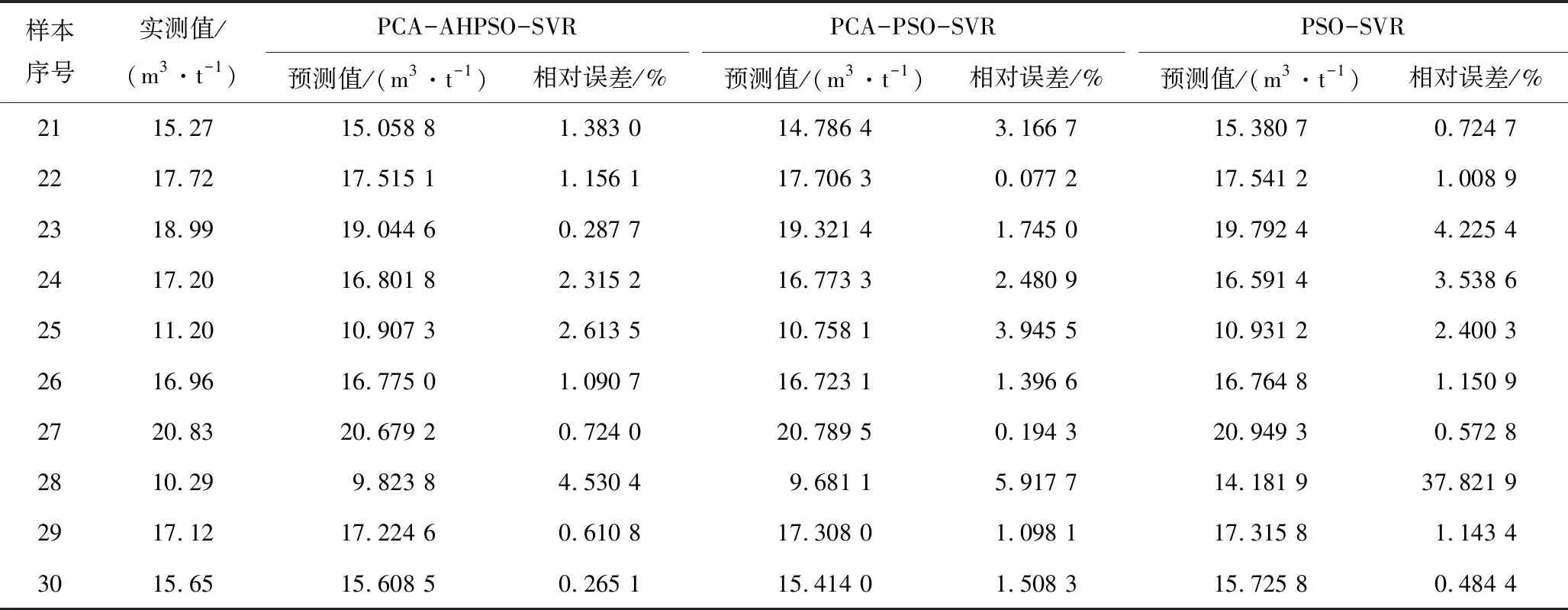
表2 预测值与相对误差Table 2 Predicted value and relative error

表3 各算法30次性能指标Table 3 30 times performance index of Each algorithm

由表2和表3数据可知，3个模型中PCA-AHPSO-SVR模型最优，预测结果更为接近实测值，PCA-PSO-SVR模型次之。

从30次运行结果看，PCA-PSO-SVR模型较PSO-SVR模型最优解和平均解均提高5%左右，由此可知，PCA降维、消除相关变量后有助于提高预测准确率，但二者对应的4个评估指标的标准差并没有显著差异，所以二者的稳定性方面并无差别；而PCA-AHPSO-SVR模型平均预测准确率达到97.18%，明显高于另外2种模型，而且对比3种模型所对应的4个评估指标30次运行结果的标准差发现，采用AHPSO算法的PCA-AHPSO-SVR模型每个指标的标准差均远小于其他2种模型，这表明AHPSO改善了PSO容易陷入局部最优的特性，是1种寻优能力更强、稳定性更佳的寻优方法，也体现了PCA-AHPSO-SVR模型良好的泛化性能、学习能力与稳定性。

4 结论

1)对粒子群算法进行了改进，构建了PCA-AHPSO-SVR煤层瓦斯含量预测模型，并应用于煤层瓦斯含量预测方面，在相同环境下与PCA-PSO-SVR模型和PSO-SVR模型分别独立运行30次，PCA-AHPSO-SVR模型计算结果平均准确率达到97.18%，明显高于另外2种模型，而且稳定性更强。

2)构建的PCA-AHPSO-SVR煤层瓦斯含量预测模型中，通过主成分分析法可以消除数据相关性，减少数据维度，降低计算难度提高预测准确率。

3)构建的PCA-AHPSO-SVR煤层瓦斯含量预测模型在学习样本附近有较高的预测精准度，大量且多样性的学习样本将有助于提高模型预测的准确性和泛化能力。