再谈椭圆和双曲线的切线的一个性质
广东韶关市九龄高级中学(512031) 何世洪
在文[1]中,齐行超老师给出了椭圆的切线的一个性质:过椭圆外一点(与焦点F1,F2共线)M作切线,切点P,则|F1M|·|F2M|=|PF1|·|PF2|+|MP|2.
在文[2]中,笔者给出了椭圆、双曲线切线的另一性质:
结论1 过椭圆=1(a>0,b>0)外一点P(x0,y0)作该椭圆的切线PA,PB,切点为A,B,则△PAB的面积为
结论2 过双曲线外一点P(x0,y0)作该双曲线的切线PA,PB,切点为A,B,则△PAB的面积为
笔者阅读文[1]、文[2]后,对严谨的论证和结论的优美倍感佩服,并深受启发,结合这两者作进一步研究,又得出了椭圆、双曲线切线的另一个性质.
性质(1)过椭圆外一点M(x0,y0)作切线,切点A,B,焦点F,则

图1
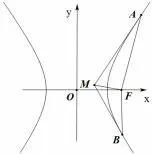
图2
证明如图1,由文[3]知,过切点A,B的直线方程为由方程组消去y,整理
得:设A(x1,y1),B(x2,y2),则

设焦点F(c,0),离心力为e,则由椭圆焦半径公式得:
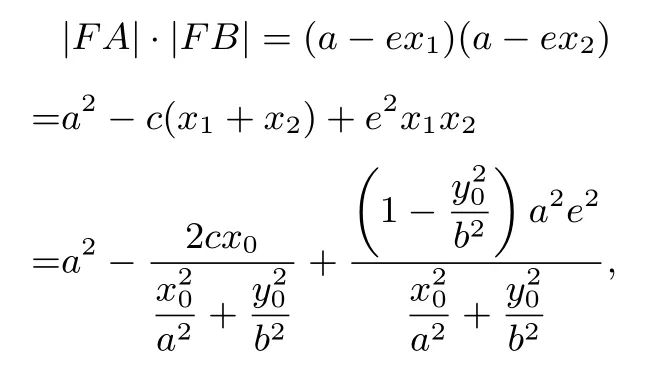
所以,
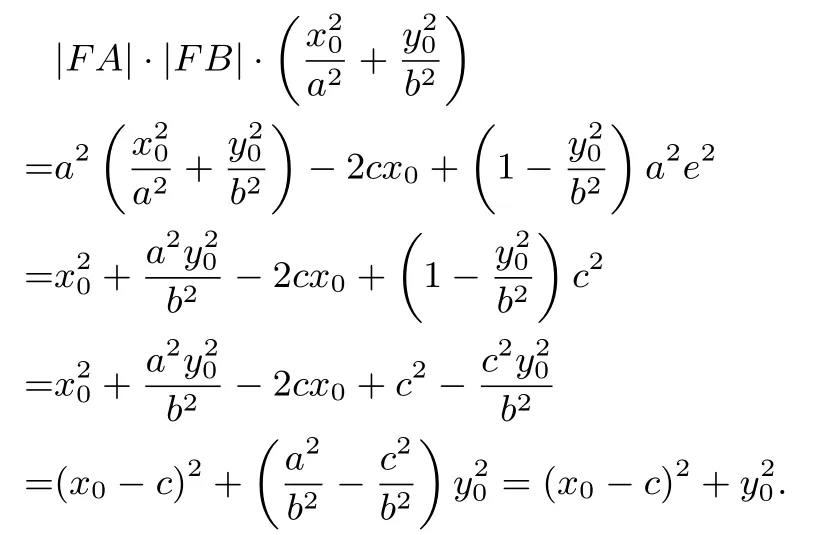
又|MF|2=(x0-c)2+y20,所以,|FA|·|FB|·|MF|2,即
(2)根据文[3]知,过切点A,B的直线方程为当切点A,B在双曲线同一支时,如图2.由消去y,整理得:

又由文[3],因直线AB与双曲线有两个同号实根,必须满足a2y20-b2x20<0,设A(x1,y1),B(x2,y2),则

设其焦点F(c,0),离心力为e,则由双曲线焦半径公式得:

因a2y20-b2x20<0,b2x20-a2y20>0,那么,

而|MF|2=(x0-c)2+y20,那么|FA|·|FB|·|MF|2,所以,
当切点A,B分别在双曲线的两支时,如图3,有上 (∗)式.由 文 [3],直 线AB与双曲线有两个异号实根,必 须0<a2y20-b2x20,b2x20-a2y20<0.同理可得,综上,有成立.

图3

