由动弦导出的向量数量积定值问题的推广

广东省湛江一中培才学校(524037) 魏 欣

题目已知椭圆的离心率为椭圆短轴的一个端点与两个焦点构成的三角形的面积为

(1)求椭圆C的标准方程;

(2)已知动直线y=k(x+1)与椭圆C相交于A,B两点.

①若线段AB中点的横坐标为求斜率k的值;

对于上述(2)的第二问,也可以这么设问：已知动直线y=k(x+1)与椭圆C相交于A.B两点.在平面上是否存在一定点M,使得为定值.若存在,请求出定点坐标及定值;若不存在,请说明理由.

1.直线所过定点在x 轴上,所对应的定点在x 轴上.

动直线l∶y=k(x-m)与椭圆b＞0)相交于A.B两点.在x轴上是否存在一定点N,使得为定值.若存在,请求出定点坐标及定值;若不存在,请说明理由.

解析设A.B两点分别为A(x1,y1).B(x2,y2),点N(n,0),则又y1y2=k(x1-m)k(x2-m)=k2[x1x2-m(x1+x2)+m2],从而消去y得关于x的一元二次方程

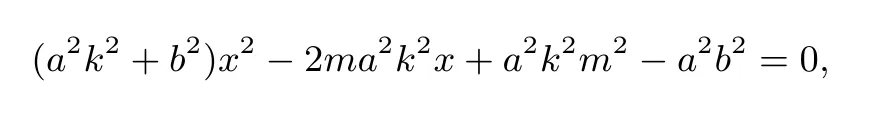
由韦达定理得

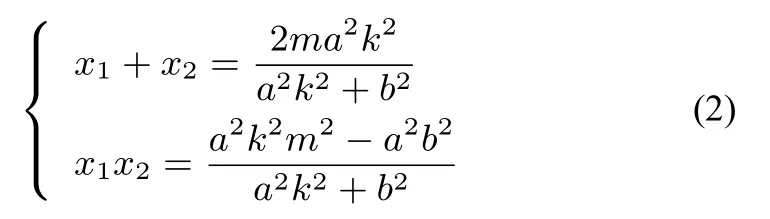
将(2)式代入(1)式得

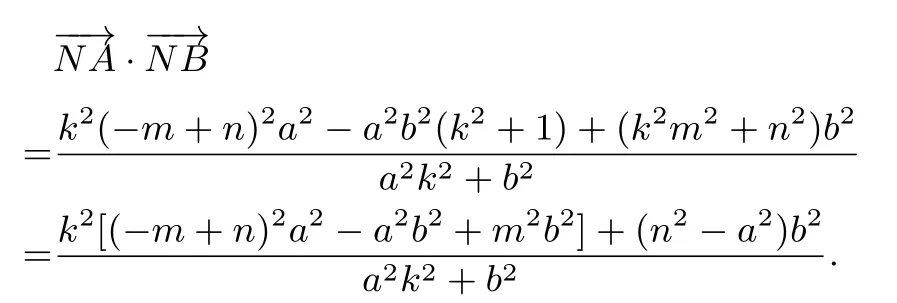
设定值为λ,则

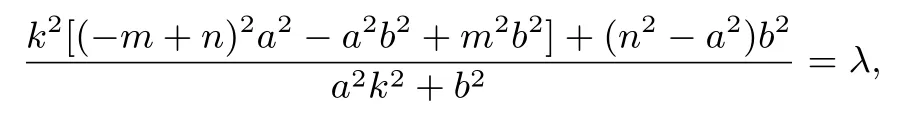
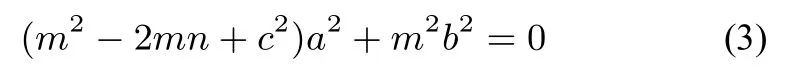
所以,当a,b,c,m,n满足(3)时,存在定点定值问题,且定点为定值为

评价对在校生的学习具有较强的指导作用，在评价中不但要遵守教学中的一般评价规则，而且要考虑如下几个方面：

2.直线所过定点在y 轴上,所对应的定点在y 轴上.

动直线l∶x=k(y-m)与椭圆b＞0)相交于A.B两点.在y轴上是否存在一定点N,使得为定值.若存在,请求出定点坐标及定值;若不存在,请说明理由.

解析设A.B两点分别为A(x1,y1).B(x2,y2),点N(0,n),则=y1y2-n(y1+y2)+n2+x1x2,又x1x2=k(y1-m)k(y2-m)=k2[y1y2-m(y1+y2)+m2],所以

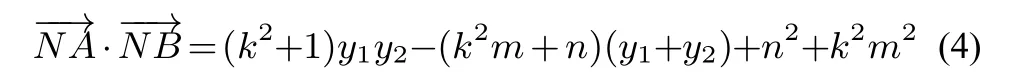
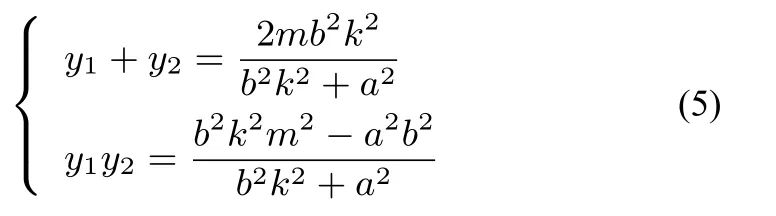
将(5)式代入(4)式得

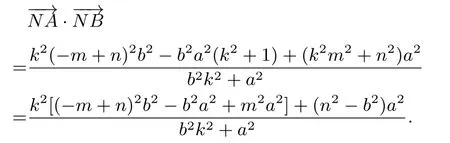
设定值为λ,则

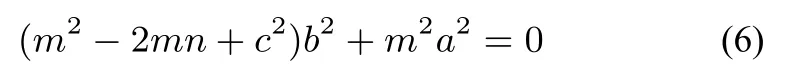
所以,当a,b,c,m,n满足(6)时,存在定点定值问题,且定点为定值为

3.一般情形.

动直线l∶y=k(x-m)+n与椭圆1(a＞b＞0)相交于A.B两点.在平面上是否存在一定点N,使得为定值.若存在,请求出定点坐标及定值;若不存在,请说明理由.

解析设A.B两点分别为A(x1,y1).B(x2,y2),点N(p,q),则又y1y2=[k(x1-m)+n][k(x2-m)+n]=k2x1x2+(kn-mk2)(x1+x2)+k2m2+n2-2mnk,y1+y2=k(x1+x2-2m)+2n,所以

将(8)式代入(7)式得

设定值为λ,得

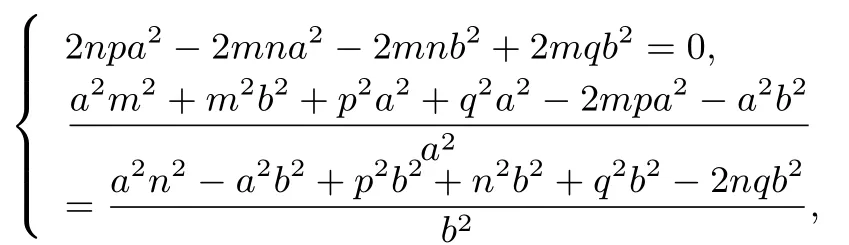
整理得,当a,b,m,n,p,q满足

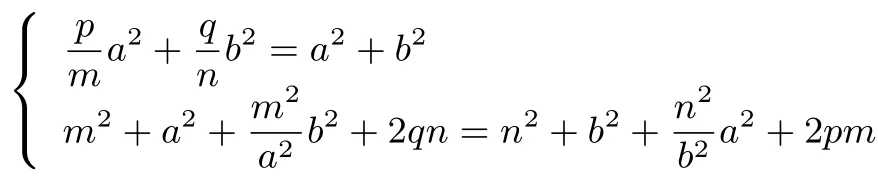
到此,本文就解决了椭圆中动弦导出的向量的数量积为定值的问题.