基于预测控制的PHEV能源管理策略∗

刘吉超，陈阳舟

(1.北京工业大学，北京市交通工程重点实验室，北京 100124； 2.北京工业大学人工智能与自动化学院，北京 100124)

前言

与内燃机汽车相比，插电式混合动力汽车(plugin hybrid electric vehicle，PHEV)在油耗和排放方面的优势得益于采用合理的能源管理策略(energy management strategy，EMS)[1]。较早被使用的EMS称为充耗-充维(charge-depleting and charge-sustaining，CDCS)EMS[2]，该策略的弊端是其节油性能会随着旅途的变长而逐渐变差。之后提出的EMS主要分为两类[1]：基于规则(rule-based，RB)的 EMS和基于优化的EMS。

RB EMS主要包括基于既定规则(deterministic RB，DRB)的 EMS和基于模糊规则(fuzzy RB，FRB)的EMS。总体上说，基于规则的策略，其规则是根据发动机Map图、人类经验和发动机的工作模式制定的，具有易实现、实时性好的优点，但它对人类经验依赖性强，很难实现油耗的优化管理。为此，后来又提出基于优化的EMS，主要包括基于全局优化的EMS和基于实时优化的EMS两类[1]。典型的基于全局优化的EMS包括：基于动态规划(dynamic programming，DP)的EMS[2]、基于庞特里亚金极小值原理(Pontryagain's minimum principle，PMP)的EMS[3]和基于遗传算法(genetic algorithm，GA)的EMS[4]。这3种EMS在旅途全局信息已知的情况下，可以实现油耗的全局最优化管理。然而，随着旅途长度的增加，它们的计算量将快速增加，严重制约了其应用的实时性；此外，在实际交通情况下，旅途的全局信息很难被提前准确获知。因此，这3种EMS可以实现离线油耗优化分析，用作其它EMS油耗优化效果的对比基准，但很难直接用于在线能源管理。相比之下，基于实时优化的EMS可实现在线油耗优化。其中，等效油耗最小化策略(equivalent consumption minimization strategy， ECMS)[5]最为典型，它主要通过调整油电等效因子来实现优化油耗的目的。然而，由于ECMS在油耗优化过程中不考虑旅途的未来信息，导致其只能实现油耗的瞬时优化。

近年来，随着预测控制研究的不断兴起，预测控制方法已成为解决复杂非线性系统优化问题的有效途径[6]。考虑到PHEV的能耗优化问题实际上属于非线性系统的优化控制问题，预测控制可将全局优化控制问题转化成在线滚动的局部优化控制问题，从而通过优化算法求解问题的最优解或近似最优解。因此，为实现PHEV能耗的在线优化，本文中提出了一种基于DP的预测控制方法。

1 车辆模型与能耗优化问题的建立

1.1 车辆模型的建立

选择并联型PHEV作为研究对象，详细的建模过程可参见文献[2]，这里直接给出车辆在离散时间状态空间内的动力学模型，即

式中：k∈[t0，tf]为行驶时间，t0和 tf为旅途的开始和结束时间；车速v(m/s)、发动机转速ωe(rad/s)、电动机转速ωm(rad/s)以及电池荷电状态SOC组成状态向量 x＝[v，ωe，ωm，SOC]T；发动机转矩 Te(N·m)和电动机转矩Tm(N·m)组成控制向量u＝[Te，Tm]T；mV，rwh，g，fr，θ，Cd，ρa和 AV分别为车辆质量(kg)、车轮半径(m)、重力加速度(m/s2)、滚阻系数、坡道角、空阻系数、空气密度(kg/m3)和迎风面积(m2)；if和ig分别为主减速器和变速器传动比；Pb，Ub，Rd，Ro和 CAh分别为电池的功率(kW)、开路电压(V)、动态内阻(Ω)、恒定内阻(Ω)和电池容量(A·h)。

式(1)中，目标转矩T与Te和Tm的关系满足：

式中ηt为总传动效率。

发动机的油耗Qf与Te和ωe的关系满足：

式中：ρf为燃油密度；Δt为当前工况持续做功时间；为制动油耗率。与Te和ωe的关系满足：

该关系可用发动机Map图描述[2]。而电动机输出功率Pm与电池输出功率Pb的关系则为

式中：ηb_dis和ηb_ch分别为电池的放电效率和充电效率；ηm为电动机的工作效率，可由关于Tm和ωm的Map图表征[2]。

1.2 能耗优化问题建立

由文献[2]可知，PHEV的能耗包括电耗和油耗。相比油耗，电耗具有零排放、低价格的优点。故以油耗作为能耗优化问题的优化目标，即

由式(3)知，Qf与Te和ωe有关。在相同的ωe下，不同的Te消耗不同的燃油。对于确定的T，可以有多种Te和Tm的组合满足式(2)，不同的Te和Tm的组合会消耗不同的电能和燃油。因此，油耗优化问题的目标就是在满足车速的前提下，确定出最优的Te和Tm的组合使J最小。

由于DP容易出现“维数灾难”和旅途全局信息在实际情况下很难获得的原因，导致其不能直接用于油耗的在线优化。故采用预测控制的思路，如图1所示，通过一个预测窗口，将油耗的全局优化问题转化成油耗的局部优化问题。于是，式(6)的最优化问题可进一步表示为

式中l为预测窗口的尺度。预测控制的目的就是在线情况下，利用DP求解出预测窗口内的最优控制量 U∗(k)使 J(k)最小，即

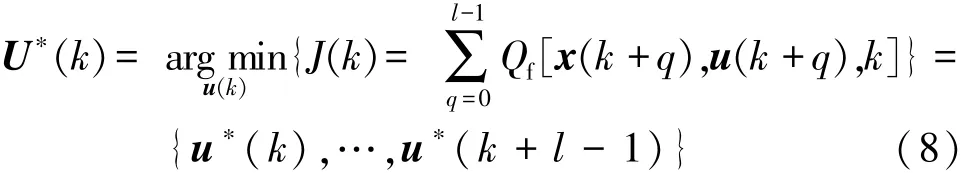
图1 预测控制思路

为实现上述控制目标，预测窗口内的车速须提前确定，下面将通过构造旅途预测模型来预测车速。

2 旅途预测模型

2.1 旅途预测原理

在实际交通环境下，单辆车的速度受到其自身运动状态和所在路段的交通状态的影响。这里选择车速v、加速度a和路段交通流速度表征车辆旅途工况的特征参数，于是得到图2(a)所示的旅途工况预测原理图。假设当前时刻为k，车辆利用由车载GPS 获得的(k)，v(k)和 a(k)去预测从第 k＋1 s到第k＋l之间的工况信息(即一个预测窗口)。这个过程中，预测窗口的工况信息可通过各个参数的预测转移关系得到，即交通流速度传输函数、车速传输函数fv和加速度传输函数fa，如图2(b)所示。因此，旅途工况预测问题可表述为

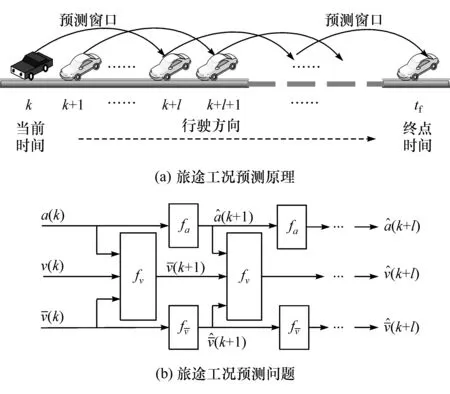
图2 旅途工况预测过程

2.2 旅途预测模型建立

由文献[7]可知，城市交通状况的混沌特性导致fv，fa和很难通过数学解析方式建立。这里以文献[7]中图1所示的北京市一条路径为例进行分析。图3给出了行驶在该路径上的某辆车从2016.7.20－2016.8.20 早高峰(7：00－9：00)时段内采集的工况信息。可以看出，v，a和的变化趋势呈高度非线性。根据文献[7]，采用反向传播神经网络(back propagation neural network， BPNN)构建 fv，fa和。由式(9)所示的fv，fa和的输入量与输出量的个数关系，确定三者的BPNN结构分别为3－5－1，1－5－1 和 1－5－1，如图 4 所示。 其中，Whi和 Who为输入层到隐含层的权值矩阵和隐含层到输出层的权值矩阵，θhi和θho为隐含层节点阈值矩阵和输出层节点阈值矩阵。为较好地表达fv，fa和的非线性特征，隐含层节点和输出层节点的传递函数分别选择tansig和purlin，于是三者的输入输出关系可表示为

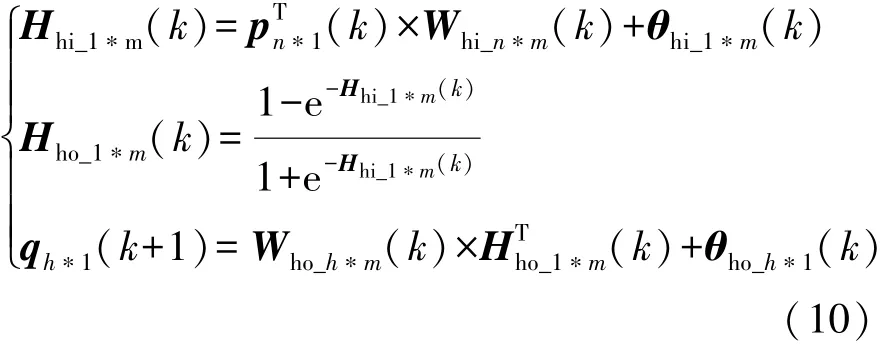
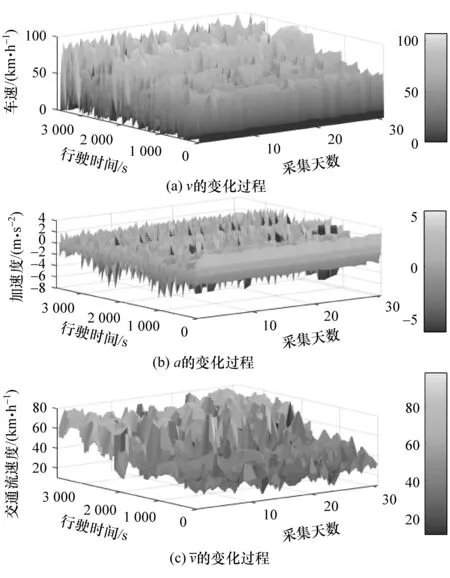
图3 采集的特征参数信息

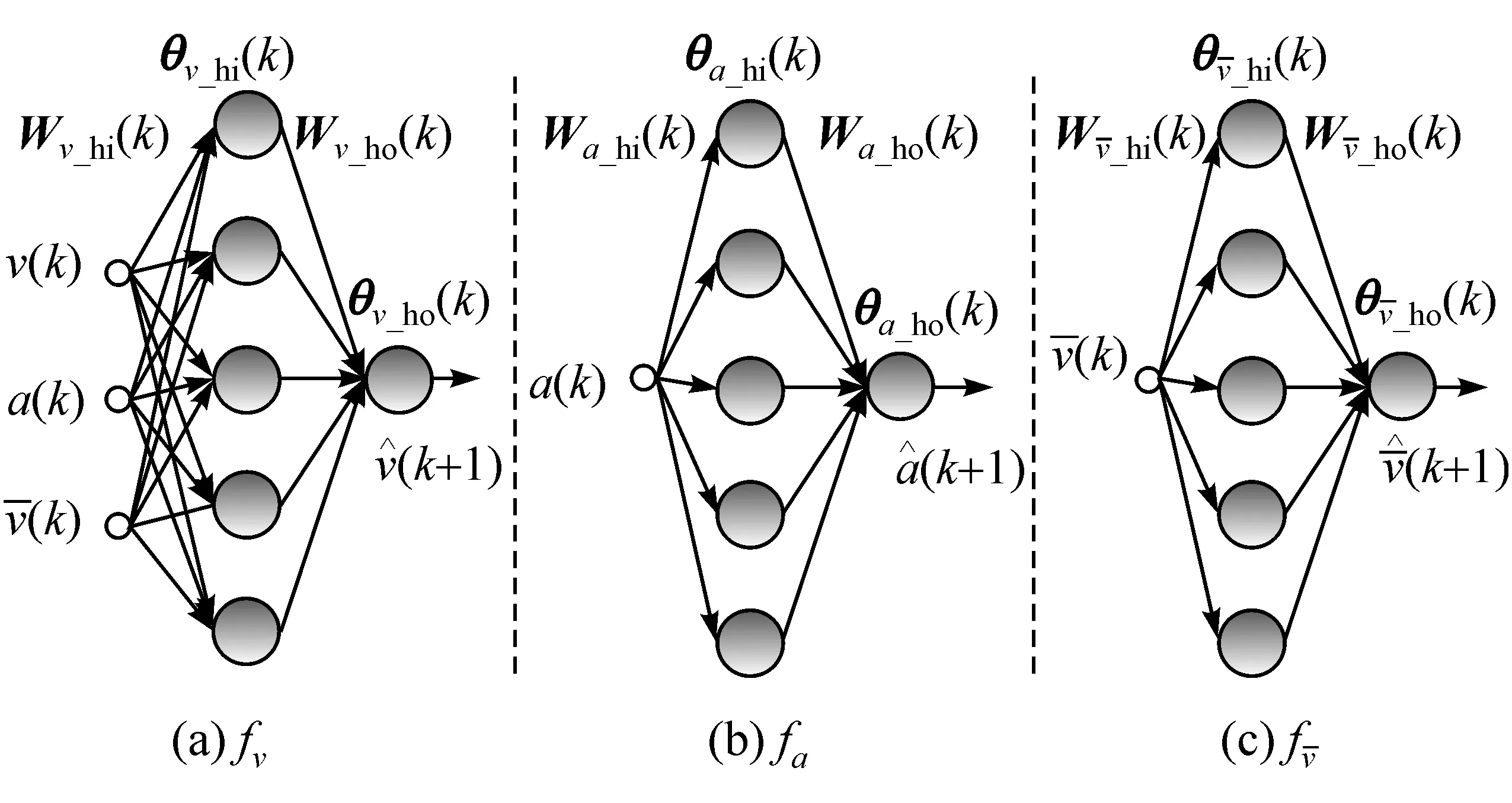
图4 fv，f v－和fa的BPNN结构

式中：pn∗1＝ [p1∗1，…，pn∗1]T∈ℝn和 qh∗1＝ [q1∗1，…，qh∗1]T∈ℝh分别为网络的输入量矩阵和输出量矩阵；m，n和h分别为隐含层、输入层和输出层的节点数。

当结构确定后，fv，fa和即可利用样本对各自的权值和阈值进行训练，直到各自的网络训练误差E满足如下条件：

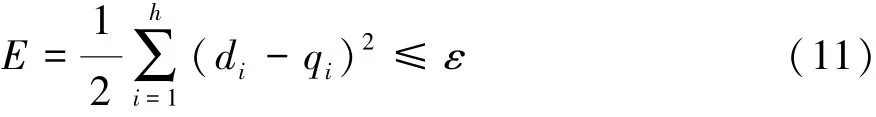
式中：di和qi分别为样本的实际值和网络的计算值；ε为网络的训练目标误差。选择带动量的梯度下降法对网络权值和阈值进行更新：

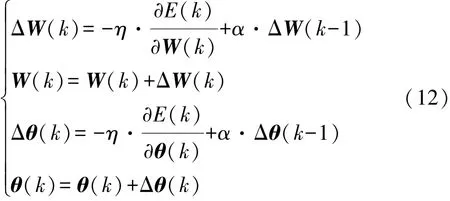
式中：η∈(0，1]和 α∈(0，1]分别为学习因子和动量因子；θ 和 W 分别为 θhi，θho和 Whi，Who的统一表示形式。通过上述方式确定出fv，fa和后，旅途预测模型便随之确定，利用此模型即可对预测窗口内的车速进行预测。

此外，根据BPNN的特性可知，fv，fa和在进行首次训练时，须对各自的权值和阈值进行初始赋值，不同的初始权值和阈值最终会影响预测模型的训练精度。为寻找最优的初始权值和阈值，采用文献[7]中提出的遗传(GA)－粒子群(particle swarm optimization，PSO)混合优化算法对fv，fa和的初始权值和阈值进行优化处理，以提高预测模型的预测精度。由于篇幅的限制，GA-PSO混合优化算法的实现原理、推导过程和具体优化流程参见文献[7]，这里不再赘述。

当基于GA-PSO的旅途预测模型确定后，即可为式(8)的求解提供预测车速。由此，预测控制即可根据求出的最优策略对预测窗口内的能源进行在线管理。

3 基于DP的预测控制策略

由上述分析可知，当车速确定后，DP即可采用后向迭代算法寻找预测窗口内的最优控制量。然而，在迭代过程中，DP的计算量会随l的增加而快速增加，导致策略的实时性变差。因此，确定合理的l和优化DP的计算过程非常重要。关于l的选择，在下一节借助具体的实验进行确定；至于DP优化算法的具体分析和实现过程参见文献[2]第4节，这里不再赘述。

此外，初始的工况预测模型是通过离线数据训练得到的。为保持预测模型对多变的交通状况的适应性，利用车载GPS在线采集的工况信息对预测模型进行在线训练更新。故设置了如图5所示的训练窗口，其中为训练窗口的尺度，表示预测模型每次完成在线训练时所需要的样本数。换句话说，当k＝时，预测模型进行在线训练更新。

图5 旅途工况预测模型在线训练原理

综上分析，基于DP的预测控制策略的实现过程如图6所示。具体分析如下：旅途工况预测模型先根据(k)，v(k)和 a(k)预测出(k)；接着，基于SOC搜索范围优化算法的 DP利用(k)计算出U∗(k)，并选择出u∗(k)送入PHEV执行，车辆随即向前行驶，k＝k＋1；同时，保存新产生的(k)，v(k)和a(k)，并判断是否需要对预测模型进行在线训练。以上过程重复执行，直至车辆到达终点。

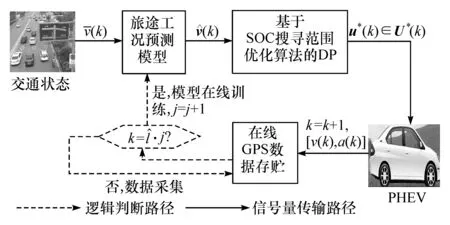
图6 基于DP的预测控制策略的实现过程

4 实验分析

4.1 实验设置

4.1.1 实验路径和样本选择

实验路径为文献[7]中的路径，fv，fa和fv－的样本如图3所示，其中训练样本和测试样本分别占70%和30%。为消除计算误差，样本在使用前进行－1～1的归一化。

4.1.2 实验参数设置

取式(12)中 BPNN 的 α＝0.05，η＝0.95，基于GA-PSO混合优化算法的初始值参见文献[7]，PHEV的参数如文献[2]中的表2所示。

4.1.3 误差评价方法

采用4种误差评价方法评价旅途预测模型的车速预测结果，即绝对误差AE、平均绝对误差MAE、均方根误差RMSE和平均相对误差MRE，具体表达式参见文献[2]中的式(32)。

4.2 车速预测分析

为验证旅途预测模型在车速预测方面的有效性，分别利用基于BPNN的旅途预测模型(模型1)、基于GA-BPNN的旅途预测模型(模型 2)、基于PSO-BPNN的旅途预测模型(模型3)和本文中设计的旅途预测模型(模型4)去预测车速。由于篇幅的限制，主要对实验路径2016年8月23－24日连续2天的早高峰时段的行车速度进行预测。经过实验，图7(a)给出真实车速与预测车速的曲线；二者之间的AE曲线以及MAE，RMSE和MRE分别如图7(b)和表1所示。

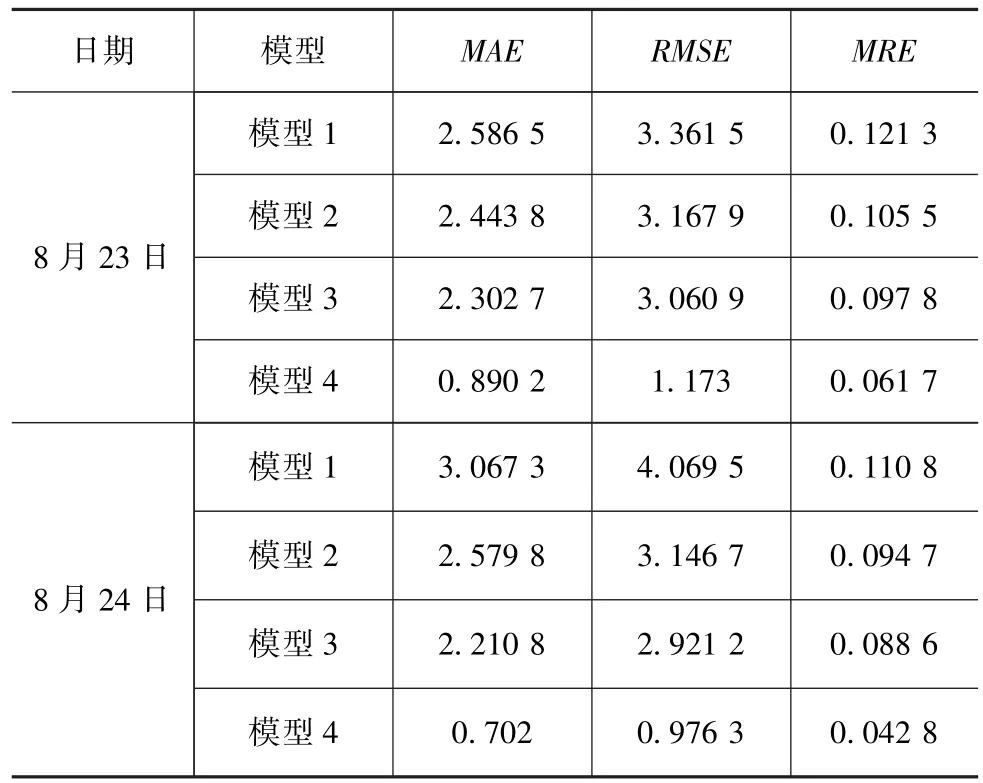
表1 预测误差

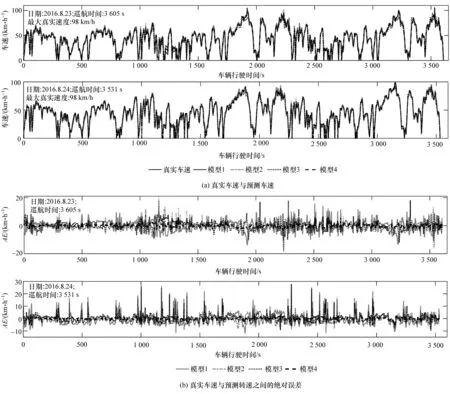
图7 真实车速与预测车速及其二者之间的绝对误差

在2个行车周期内，首先，如图7(a)所示，4种模型预测的车速变化曲线均可跟随真实速度的变化趋势。其次，从图7(b)给出的AE可知，模型1～4在8月 23日对应的 AE范围分别为[－13.71，14.98 km/h]，[－12.28，20.59 km/h]，[－18.44，18.12 km/h]和[－3.92，11.05 km/h]，在 8月 24日对应的 AE 分别为[－11.75，26.93 km/h]，[－9.26，11.24 km/h]，[－10，27.89 km/h]和 [－6.05，3.68 km/h]；相比之下，模型4的AE明显比其它3个模型小。此外，如表1所示，模型4对应的MAE，RMSE，MRE也比另外3个模型小；以8月24日为例，相比于模型1～3，模型4的MAE，RMSE和 MRE按次序分别降低了 77.1%，72.8%，68.2%，76%，69%，66.6%，61.4%，54.8%，51.7%。 此外，模型 4在2个行车周期内的车速预测精度(即1－MRE)超过了93%。

综上分析，本文中提出的旅途预测模型可有效实现车速预测，预测精度较好。

4.3 策略性能分析

图8 l和的分析过程

4.3.2 策略分析

为验证策略的有效性，同时对CDCSEMS(记为EMS－1)，FRB EMS(记为：EMS－2)，ECMS(记为EMS－3)和基于DP的全局优化EMS(记为EMS－4)及基于DP的预测控制策略(记为EMS－5)进行了仿真，仿真结果选择图7(a)中模型4在8月23日预测的车速。SOC的初始值和期望终值分别设为0.8和0.2。经过实验，5种EMS对应的T和 T的结果如图9所示。下面对不同策略的性能进行对比分析。

表2 5种EMS的电动机和发动机的平均效率 %

其次，5种EMS对应的总能耗、电耗、油耗和排放情况如表3和表4所示。表3中的CT，CE，Cf，PDE和PDf分别表示总能耗、电耗、油耗、用于驱动的净电能量和用于驱动的净油耗能量。为进一步对比策略的性能，同时对一台70 kW/150 N·m的内燃机汽车(ICE-V)进行了仿真。

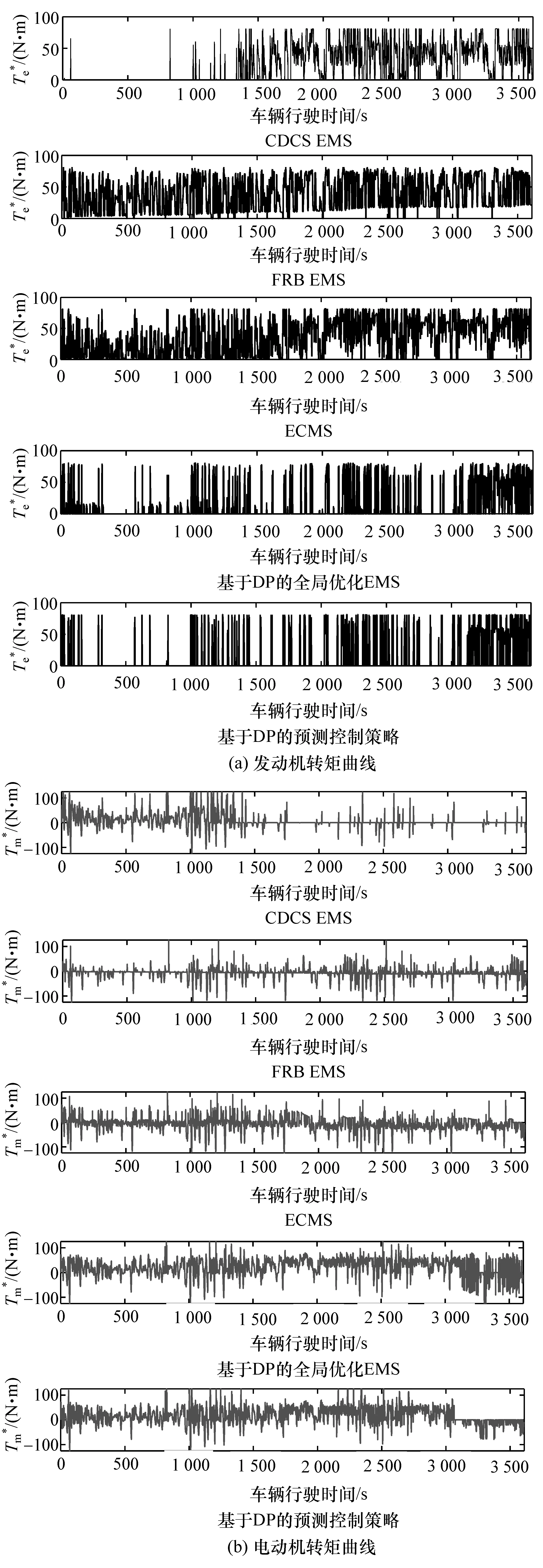
图9 5种EMS对应的T和T的结果曲线

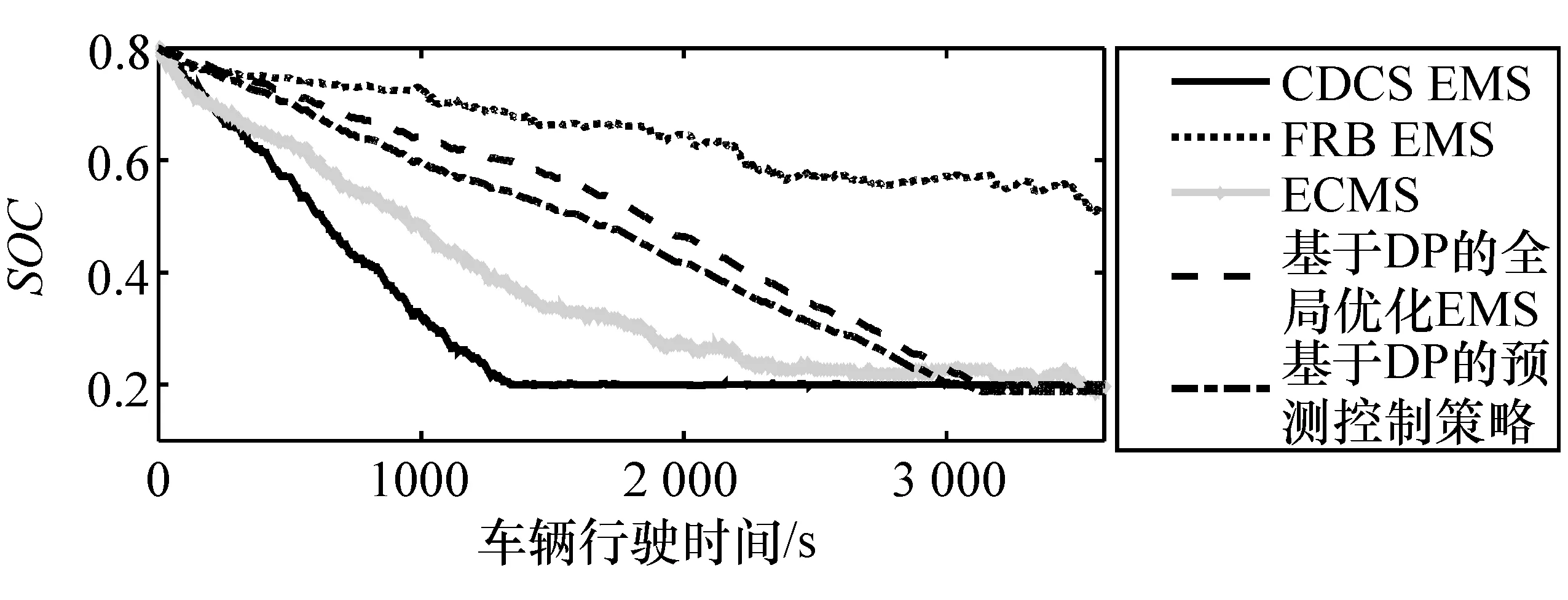
图10 5种EMS对应的SOC变化曲线

表3 5种EMS的能耗情况

表4 5种EMS的排放

由表3和表4可见，相比于ICE-V，5种EMS的油耗分别降低了 24.7%，12.5%，28.5%，36.4%和32.8%；对应地，5种 EMS的排放(即 HC，CO，NOx)也得到不同程度的降低。为分析本文中提出的策略与全局优化的EMS之间的性能差别，表3和表4分别给出了两者的能耗和排放结果。相比于基于DP的全局优化EMS，基于DP的预测控制策略的油耗增加了5.6%，且排放也有不同程度的增加；但是，基于DP的预测控制策略可在1 s内完成单个预测窗口的能耗优化，而基于DP的全局优化EMS的优化时间超过了12 h。此外，与实时策略 CDCS EMS，FRB EMS和ECMS相比，基于DP的预测控制策略的油耗分别降低了10.8%，23.3%和6%，对应的排放也有不同程度的降低。第4.2节提及模型4预测车速的精度超过了93%，为分析这不足7%的车速预测误差对策略的影响，利用所提出的EMS对8月23日和8月24日的真实车速进行了仿真。预测车速和真实车速对应的能耗和排放如表5所示。可以看出，与真实车速相比，预测车速的油耗分别高出6.88%和0.08%，对应的排放也有不同程度的增加。后经分析得知，8月23日为雨天工作日，而8月24日为晴天周末，这说明天气状况和是否为工作日对策略的优化效果产生了一定的影响，但总体而言，提出的策略可较好地反映出真实车速对应的能耗情况。

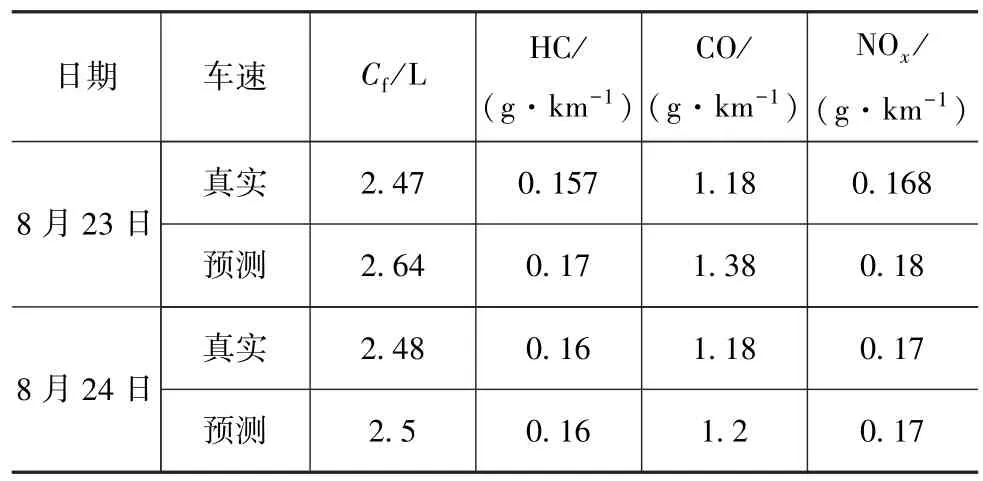
表5 预测车速与真实车速的能耗和排放

综上分析，在能够反映实际车辆能耗的前提下，所提出的策略油耗和排放虽然比基于全局优化的EMS略差，但是其具备出色的实时性；同时，与现有实时策略相比，其油耗和排放得到了改善。

5 结论

针对PHEV的能源在线优化问题，设计了基于预测控制的能源管理方法。该方法首先构造了基于GA-PSO混合优化算法的旅途预测模型；在此基础上，设计了基于DP的预测控制策略。经过实测数据仿真验证，得到以下结论。

(1)设计的旅途预测模型可有效地实现车速预测，预测精度达到93%以上；且该模型的预测车速对应的能耗可有效反映出真实车速的能耗情况。

(2)相比于全局优化EMS，虽然设计的EMS很难实现全局能耗优化，但它具有良好的实时性，方便PHEV的在线应用；同时，其油耗和排放比现有的实时策略低，有效地改善了PHEV的能耗表现。