十二平均律三四度循环分律法
文/郑怀杰
钢琴作为击弦类键盘乐器,所采用的律制是十二平均律。在钢琴调律过程中,基准音组分律的准确程度,将决定整台钢琴的音准是否能符合要求。
如果基准音组分律不准确,向高音区和低音区扩张过程中的过渡性、和谐性、准确性将会受到很大影响。因此,作为钢琴调律工作者,无不把基准音组十二平均律的划分作为一项极其重要的环节加以重视。
自从18世纪以来,人们开始了在乐器上采用十二平均律,律学实践者在十二平均律划分中做出许多探索和研究,力求把理论数据在听觉效果上作出充分体现,从而在钢琴调律过程中出现了多种基准音组的划分方法。诸如:四五度调律、三六度检验法、三六度调律、四五度检验法等,试图寻找最科学合理切实可行的分律法。这些分律手段尽管方式不一,其目的也较为一致,每种分律法都有其合理性,在实践中也可行,但也各有不足之处。在以往的有关钢琴调律方面的文献中有所记载,这些方法经常会不同程度出现音高和音程关系上混乱的现象。长期的调律实践中,我发现采用十二平均律三四度循环分律法更为科学、合理,会有效避免音程交叉进行时,听觉混乱现象的产生。在此我提出个人看法,供同行参考,请大家指正。
1.以往对音高的标注:
如:(33F、45F、37A、43D)等,其中阿拉伯数字表示钢琴琴键位置的序号。这样的标注只是钢琴生产工艺中对琴键的排列,便于生产和装配,一般的钢琴都是88键,也有的钢琴是97键等等。所以不能说明某个序号的琴键就是代表某音的高度。在数字的后方,一般都是用大写的英文字母表示,分不清该字母代表那个音区的某个音高。
2.以往对音程的标注:
以33F—38♯A为例, 其标注音程为四度,实际为增三度。
38♯A—45F为例, 标注音程为五度,实际为减六度。
36♯G—40C,38♯A—42D为例, 其标注为大三度,实际为减四度。
这样的标注,虽说音程关系是相等的,但是音程的性质则完全不同。
3.以往对升降记号的使用:
有些调律文献中四五度分律法以上四、下五分律程序中多使用升记号。
以33F—38♯A,38♯A—45F为例。前面已经对其音程关系以及音程的性质作过表述,不再重复。现在就升降记号的使用提出不同看法。
基本乐理中有过明确表述,如果从某一律音出发向上按照五度级生律,则采用升记号;而从某一律音出发向下按照五度级生律,则采用降记号。谱例中明确表示是以上四、下五进行基准音组分律的,其中上四也就等同于下五,因此在记谱中应该使用降记号而不是升记号。反之,基准音组分律中采用上五、下四的分律方法则应该采用升记号。
这种关于音高、音程以及升降记号的标注方法,只有钢琴生产人员以及钢琴调律人员知道其中意思,可是作为音乐工作者来讲并不能明白其中含义。因此,我认为所有关于音高、音程以及升降记号的标注一定要规范科学,更不能有概念性错误,我在本文中有关音高、音程以及升降记号的标注都做了改变。在此基础上,我总结出一种更加合理更加有效的十二平均律三四度循环分律方法(见图1)。
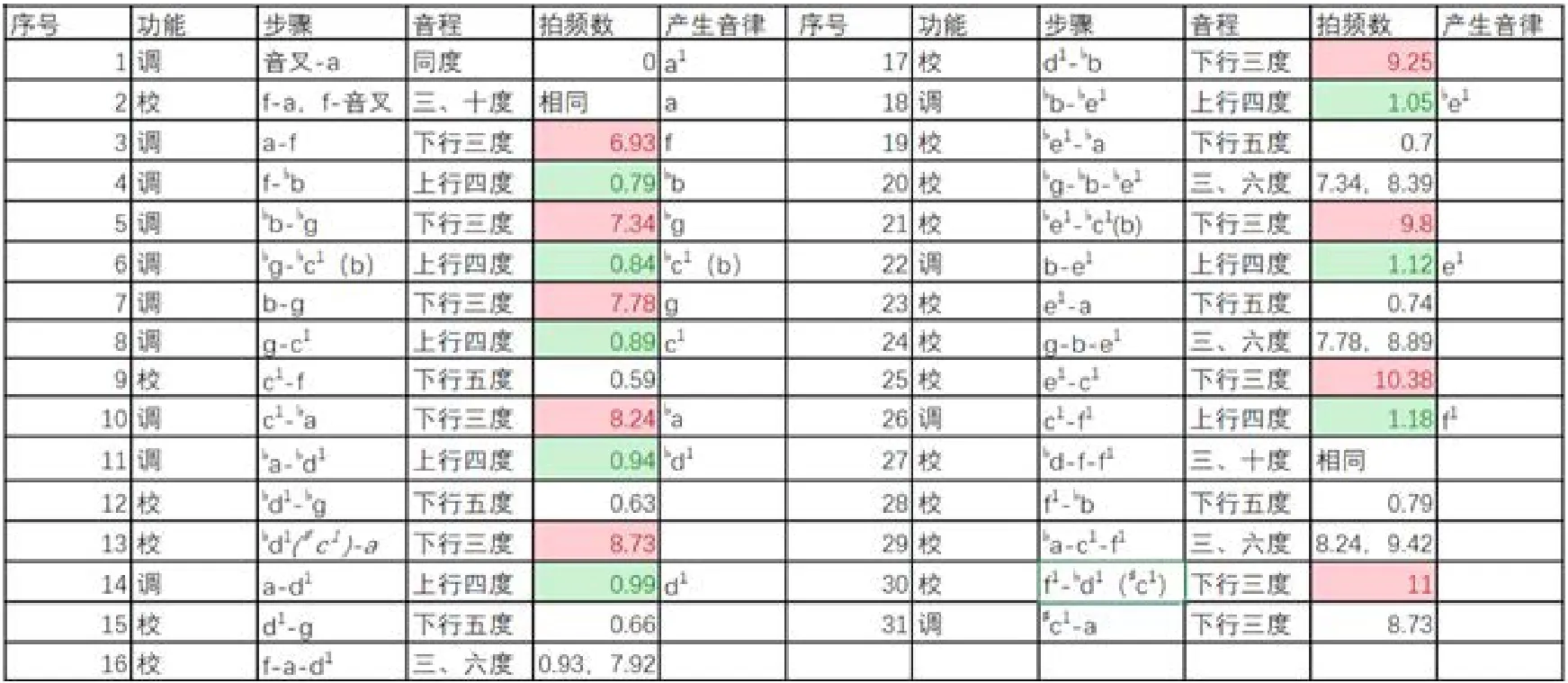
图1
从图一我们可以清晰地看到,三四度分律法的所有程序。为了能证明此种分律法既符合十二平均律的理论,同时又具有实际操作的可行性,我从以下几个方面进行论述。
(一)三四度循环分律法的理论数据分析
既然是三四度循环分律法,首先要看大三度、四度在十二平均律中所处的地位及功能。先了解一下大三度(见图2)。
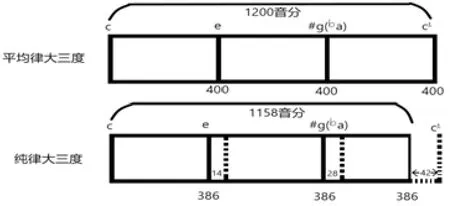
图2
十二平均律大三度是400音分,400×3=1200音分,也就是说三个大三度构成一个八度。纯律大三度为386音分,386×3=1158音分,(400-386=14音分)纯律大三度比平均律大三度小14音分。(1200-1158=42音分)纯律三个大三度之和比十二平均律八度小42音分。
如果我们把纯律大三度作为参考点,把纯律大三度每次增加14音分,连续3次就能构成十二平均律八度。当然,要把理论值经过听觉的调整和实际操作才能达此目的。我们在操作中需要利用纯律大三度听觉上的纯点调整到和十二平均律大三度一样的高度,将一个八度均分为3个等份。固定一个八度中c、e、♯g、(♭a)、c1的位置。但大三度有其局限性,从某一律开始按三度级的生律方法,无论怎样也生成不了十二平均律中的其它九个半音(见图3)。
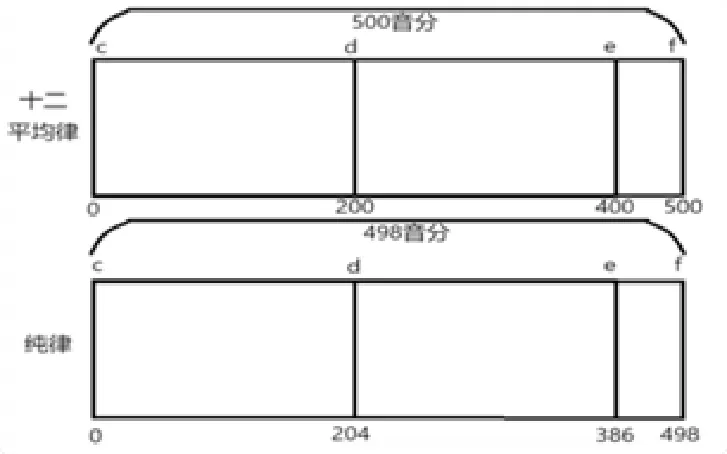
图3
十二平均律四度为500音分,纯律四度为498音分,纯律四度小于十二平均律四度2音分(“小微音差”)。如果利用纯律四度生律,从某律开始连续进行12个四度级,不能够完全回到始发律。连续生律12次,每次比十二平均律少2音分,2×12=24音分,也就是说累计少了24音分(“最大音差”)(见图4)。
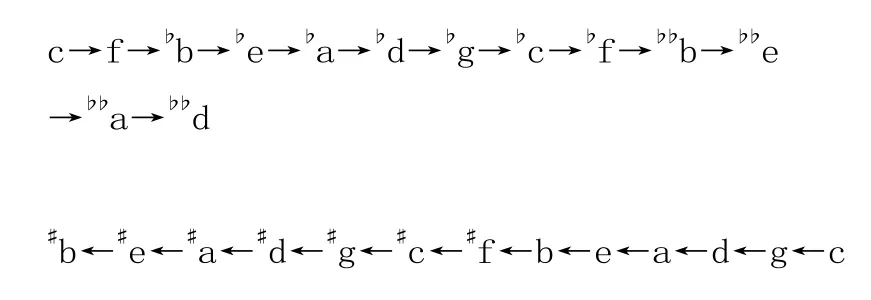
图4 四度生律
用纯四度分律时,为了达到十二平均律的音高要求,就必须每次进行一个四度就需要增加2音分,经过12次生律后就生成了十二平均律的12个半音,归纳在一个八度内构成十二平均律所需的音准高度。
四度生律优点在于:1.四度音程是五度音程的转位音程,从某音上行生成四度,实际就是从某音开始向下生成一个五度。用四度生律可以回到始发律,完成循环过程。2.在循环生律过程中可以生成十二平均律所需的十二个半音。3.在基准音组分律过程中,平均律四度在听觉上属于协和音程。拍频在每秒1拍左右,便于听辨。
我们得知:利用大三度生律3次可以回到始发律,建立一个八度内三度音的固定位置。利用四度生律12次不但可以回到始发律,而且可以生成十二平均律所需的十二个半音。大三度、四度、五度、大六度这四种音程是基准组分律中常用的调整和检验的音程。利用三四度分律法进行分律过程中已知音程有大三度、四度,同时我们知道四度的转位音程是五度,大三度加四度构成大六度,满足了分律过程中所需要的条件。综上所述,三四度分律法具有为十二平均律分律的可靠理论依据。
(二)三四度循环分律法的循环联接实践
任何一种分律方法,除了具备理论依据外,还必须能够形成循环联接。我们这里所讲的循环还有别于理论上的循环,是在实践过程中的循环。要完成十二平均律分律,首先需要选择合适的音区,在一个八度内完成此项工作。无论哪种分律法,都必须遵循一个原则,那就是“循环”。所谓“循环”就是说从某一律音开始,经过多个步骤后必须回到始发音。以往多种分律法都具备了这一条件,但是在完成“循环”的过程中,有些步骤是跳跃性的。这些步骤都对操作循环的流畅性、听觉上的过渡自然性以及对拍频的把控有一定困难。用三四度音程交替进行,可以形成有效的循环联接,操作程序合理,实用性强。
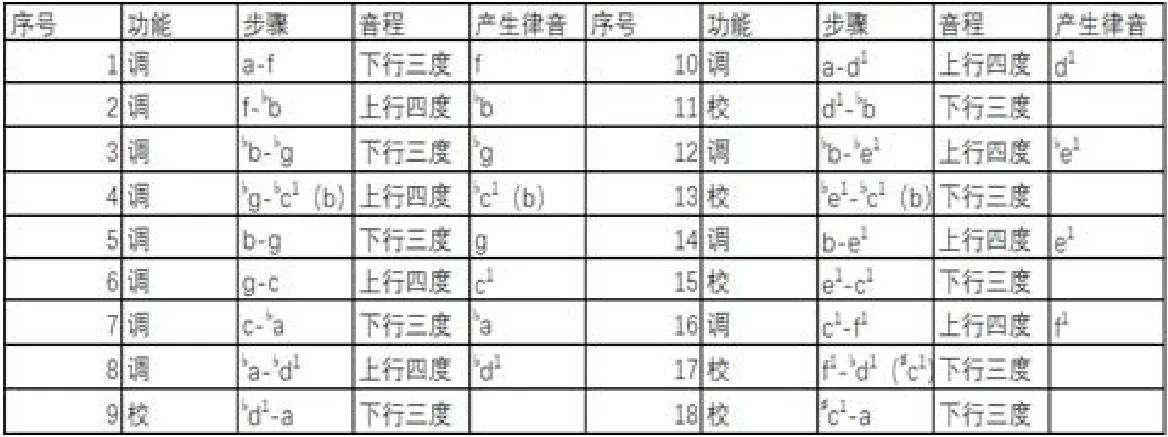
图5

图6
上图表明,三四度分律,从a开始,经过18次程序(不包括有些检验程序)生成了12个半音,其中6个核对程序是借助已经生成的律音再生下一律音的。
在分律进行过程中,按照下行三度、上行四度原则进行的逐步推进,音程没有跳跃性,保证了听觉上的自然过渡。
从某音开始生律,始终按照下三度,上四度的规律进行,环环相扣,形成循环联接。
以上三点说明:三四度分律法循环联接合理、生律规律性强。
(三)三四度循环分律法的拍频渐进特征
在实践过程中,我们是利用听觉来辨别该音所处的位置,音程的大小,在理论上是用音分来区别的,但是在听觉上,调律师是借助拍频来体现的。让我们来看一看平均律大三度、四度的拍频是怎样产生的。
我们已知纯律大三度频率比是5/4,如果以a1的频率440Hz为标准音,根据八度的频率比1/2的原则,要得知a的频率。就以440×1/2=220(Hz)要求得a的下方大三度的频率,已知条件:a=220Hz;f=174.614Hz。频率比:5/4,220×4-174.614×5=880-873.070=6.93.平均律大三度大于纯律大三度。因此平均律大三度的拍频是+6.93拍/秒
求f的上方四度的拍频:已知条件:f=174.614Hz,♭b=233.082,频率比为4/3,就以233.082×3-174.614×4=699.246-698.456=0.790(Hz),十二平均律四度大于纯律四度。因此平均律的拍频是+0.79拍/秒。
查看图7不难发现,一个八度内共有9个大三度,其中大三度从第一个f-a(拍频6.93)到第九个♯c1-f1(拍频11.00)。一个八度内共有八个四度,从第一个f-♭b(拍频0.79)到第八个c-f1(拍频1.18)。
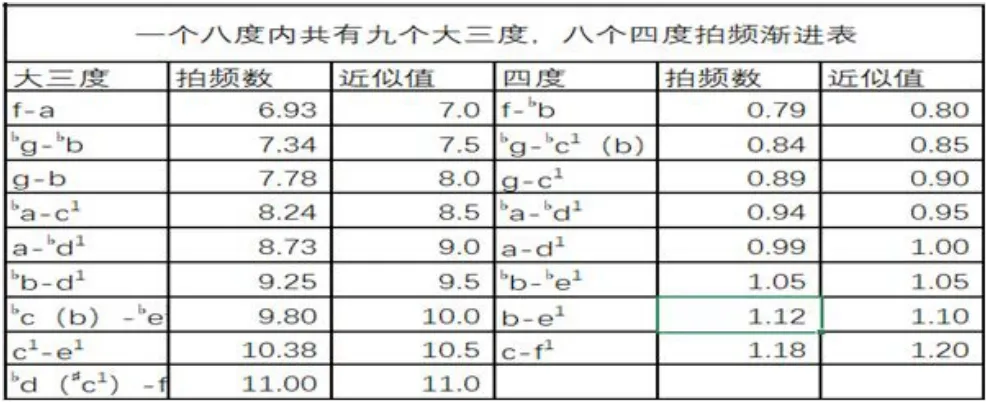
图7
每个半音向上大三度或四度的拍频都依次渐快,很有规律。我们在实践过程的分律程序也是依次从f-f1进行的。也就是说,三四度分律法的程序和三四度拍频速度是渐进的,为我们更好的掌握此项技术提供了便捷的途径。
我们看到上图中十二平均律中各音程的拍频数,虽然有一定的规律性,但是要做到如此准确,在实际操作中还是很困难的。我在表中拍频数一栏的后面加上一栏,其中把各音程的拍频数进行简化。比如大三度f-a的拍频数6.93简化为7.00,后面的大三度音程依次为7.50、8.00、8.50……,以0.5递增。四度音程的拍频也做了同样的处理,相邻半音向上四度,每级以0.05递增,以便于调律师在实际操作过程中更好的把握各音程的拍频。
图七表格中计算的各音程拍频,是理想条件下得出的理论数据。现实情况中,钢琴的尺寸,弦列设计以及结构的差异,都会不同程度地对各音程的拍频产生影响。所以此表格仅作为理论参考,调律师应在保证大三度和纯四度音程拍频递进的情况下,根据钢琴音响的实际状况对部分音程的拍频进行适当的修正,以达到更好的音准效果。
(四)三四度循环分律法检验程序的效果
任何一种分律方法,都要有充分的检验程序。在分律过程中,每当调整一律音后,必须和先前已经调整的某一律音形成有效的音程检验。检验的目的是看当下调整的律音和形成检验音程的某一律音是否符合要求,不能单看某一个律音的位置,两者都要检查。在检验过程中,不完全是听音程的协和程度,主要是听拍频的准确性,不时和邻近的音程相比较。关于检验音程及其步骤请看图8。
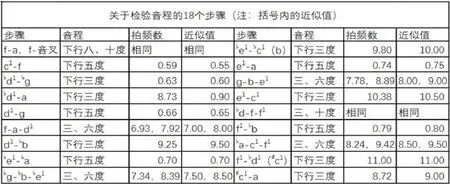
图8
在三四度循环分律法中,调整和检验的关键点是以下几个(参考图1):
1.步骤(1)确定标准音的准确性。
2.步骤(13)保证♭d1(♯c1)位置,是f-a-♭d1(♯c1)-f1连续三个大三度中的第三个关键点。♭d1(♯c1)-a(大三度),♭d1-♭g(五度),♭a-♭d1(四度)这几个音程的拍频都符合要求,则说明步骤(3)a-f(三度)中的f音律高度和其它律音高度基本不存在问题。
3.步骤(16)检验确保d1的准确性。因为f、a两音已经检验过,那么f-a-d(三六度)检验拍频符合要求,更进一步证明前面的调整和检验是成功的。
4.步骤(20)♭g-♭b-♭e1(三六度)检验,巩固了以前工作的成果。
5.步骤(24)g-b-e1(三六度)检验成立证明,b-e1(四度)e1-a(五度)和先前调整g音的高度是没有问题的。
6.步骤(27)♭d-f-f1(三、十度)检验后,可以确认f到f1的音律高度正确。
7.通过步骤(30)(31)从f1-♭d1(♯c1),c1-a,两个下行三度的检验,让♯c1-a拍频正确,再次确认♯c1音高,可以肯定在从f-a-♯c1(♭d1)-f1的大三度连续生律的第二次生律是准确的。至此,我们认为,a开始向下生一律产生f,从a开始向上生一律产生♯c1(♭d1),♯c1(♭d1)向上再生一律产生f1,和f-f1的八度音程准确,再次证明大三度分律在三四度分律法中的重要性。
在步骤(31)中♯c1-a下行三度,让从a开始一系列分律及检验程序后又回到a音,完成了循环分律的过程。
综上所述:在十二平均律基准音组分律中,调整是手段,检验是确认,准确是目的。
十二平均律三四度循环调律法,在基准音组的分律中,具有可靠的理论依据,循环联接的程序、拍频渐进的听觉效果及充分的检验手段,实属便于实操的新分律方法。
——探究李斯特钢琴曲《魔王》

