基于微地震定位和速度成像的页岩气水力压裂地面微地震监测

缪思钰,张海江,陈余宽,谭玉阳,苗园园,黄振华,王 飞,谢庆明

(1.中国科学技术大学地球和空间科学学院万泰微地震实验室,安徽合肥230026;2.安徽万泰地球物理技术有限公司,安徽合肥230026;3.重庆地质矿产研究院,重庆401120;4 重庆华地工程勘察设计院,重庆404100)

水力压裂是低渗透油气藏改造的重要手段,通过在目标储层产生新的裂缝网络,为低孔隙油气藏提供油气运移的通道[1-6]。伴随破裂区内裂缝的生成或已有断层的活化,会发生一系列微弱地震事件。对这些微地震事件进行监测,从而刻画裂缝的形态分布[7-10]及发育过程[11-13]、描述裂缝间的相互作用[14-15]、估算储层改造体积[16]、进行储层应力分析[17]和开展地震灾害评价。

微地震监测通常采用两种方式:井下监测[15,18-20]和地面监测[3,21]。对于井下微地震监测来说,受地表噪声影响较小,监测记录信噪比相对较高。但由于检波器仅分布在狭窄孔径中,且数量有限,空间覆盖范围小,导致水平方向上的分辨率有限,定位难度增加。在这种情况下,可以通过P波传播方向来确定事件方位角[22-23]。目前大多数定位方法利用P波极性来计算微地震事件方位角,并结合P波和S波到时确定事件的位置。如果压裂井附近不存在邻井,地面监测就成为唯一选择。目前,地面微地震监测主要有两种布设方式。一种方式是在地面布设大量的检波器[2]。为了达到经济和高效的双重标准,采用星状排列地表监测系统。当检波器数目一定时,该方法能更加有效地扩大检波器覆盖范围。星状地面微地震监测需要采用扫描叠加的方式提高弱事件的信噪比才能对微地震事件进行定位。除此以外,可在已知的震源区域上方采用适当增加检波器个数,提高该区域的分辨率[24]。另外一种监测方式是在浅孔中布设传感器。由于传感器埋设在浅孔中,可以大大降低噪声水平,因此采用较为稀疏的浅孔传感器台阵就可以监测微震事件并对其进行定位。与井下微地震监测相比,地面监测的定位结果水平分辨率更高,但在深度上的分辨率较差[3]。

对于水力压裂来说,确定压裂裂缝分布以及压裂储层改造体积对于油气藏开发非常重要。微地震监测资料处理的一般流程是:首先进行微地震事件检测,再对检测出的事件进行定位,最后根据微地震事件的空间分布来描述裂缝分布和估算储层改造体积[25-27]。因此,对微地震定位精度的要求较高。但由于微地震信号较弱,接收到的数据信噪比通常较低[28],造成提取初至到时存在一定误差。为了降低该误差,可以基于不同微地震事件到同一台站波形的相似性采用波形互相关技术来提高到时拾取的准确性,获得精度较高的相对到时[29]。相对于基于绝对到时的定位方法(例如网格搜索法),双差定位方法[30]可以直接利用相对到时对微地震事件进行定位,获得高精度的相对定位,使原本较为发散的定位结果变得更加收敛。在双差定位算法的基础之上,ZHANG等[31]发展了双差地震成像方法,在提高地震定位精度的同时,可以确定震源附近的速度结构。

由于微地震信号通常十分微弱,无法全部被识别出来,因此,压裂储层体积不能仅依靠微地震事件的空间分布来计算。对于水力压裂来说,在目标储层产生了裂缝,并且裂缝中充满流体或者气体,造成压裂改造后的储层物性与周围储层相比会发生明显变化。例如,由于裂缝以及流体或气体的存在,会导致地震波传播速度降低。因此,结合微地震事件的空间分布和速度成像结果可以更加可靠地估算储层改造体积。对于井下微地震监测,CHEN等[32]发展了基于微地震事件反方位角信息及到时差的双差地震成像方法,在实现定位的同时,确定了目标储层的速度结构,发现微地震事件和低速异常之间有很好的关联性。

本研究首次将双差地震成像算法应用于国内某地区页岩气水力压裂地面微地震监测数据。利用微地震事件对的相对到时,同时反演三维速度模型和震源位置。相较于传统的定位和成像方法,本文方法对震源区的速度变化约束能力更强,定位结果更精确。

1 双差地震成像算法

双差地震成像算法[31]是在双差地震定位方法[30]的基础上发展而来的。该方法在利用绝对到时确定震源绝对位置的同时,用更加精确的相对到时减少到时系统误差,能够得到更加精确的速度模型和震源位置。

(1)

(2)

式中:Δxl(l=1,2,3)和δu分别表示震源位置在三分量上的扰动和沿着射线路径的地震慢度扰动。

对于地震事件对i和j来说,(2)式表示事件i到台站k的理论与观测到时差,将(2)式减去事件j到同一台站k的理论与观测到时差,可以得到:

(3)

(4)

(5)

(5)式即为双差地震定位公式。

对于基于公式(3)的双差地震成像算法,两个相近事件的射线路径大致重合,(3)式中的速度模型扰动项在震源区外几乎可以完全去除。双差地震成像的优点是可以利用相对到时确定震源区的速度异常,而对于震源区之外的速度异常,可以采用公式(2)给出的基于绝对到时的地震成像算法确定。双差地震成像系统实际包含了公式(2)和公式(3),用绝对到时来反演震源区之外的速度结构,用相对到时来反演震源区内的精细速度结构[31]。鉴于震源位置和速度结构存在耦合效应[33],我们同时反演相对位置、绝对位置以及速度结构。双差地震成像通过调整速度结构来提高地震定位精度,再通过提高定位精度来降低反演速度模型的误差。因此,与传统的定位和成像方法相比,双差地震成像能够更加准确地反演地震位置和速度模型。

2 地面微地震监测数据

利用我国西南地区某垂直井的水力压裂地面微地震监测数据进行定位和速度成像研究。该压裂井位于一个逆冲断夹片构造带,是一口页岩气预探井,目的层平均倾角约为60°,岩性以黑色碳质页岩、灰质页岩为主,底部为一套硅质岩沉积,夹少量薄层粉砂岩和粉砂质泥岩。目的页岩层主要发育块状层理和水平层理。该井在纵向上非均质性强,岩性复杂。本次压裂施工分为5段,压裂深度范围在平均海平面以下600～1800m。

地面微地震监测系统采用了28个4.5Hz的三分量传感器,采用浅孔(大约5m)布设的方式进行安装。台站位置如图1所示,其中蓝色三角形表示检波器的布设位置,黑色圆点表示井口位置。记录的采样率为1ms。首先采用声波测井曲线建立一维速度模型,并采用射孔信号对初始速度模型进行了校正(图2)。利用长短时窗法检测出1400多个微地震事件,从中挑出了信噪比较高的962个事件进行定位和成像。

图1 地面微地震监测台站分布

在人工提取绝对到时的基础上,为了减小拾取误差对地震定位和成像的影响,我们采用波形互相关法计算了地震波之间的到时差。对于震源位置和破裂机制相似的两个地震事件,由于震源到台站射线路径相似,它们到达同一台站的波形也具有较高相似度[34]。因此,采用波形互相关可计算同一震相到达不同台站的到时差。按照人工拾取的P波到时,对地震波形记录对齐(图3a),可以看出,由于微地震信号能量小,信噪比较低,P波初至处没有明显起跳,人工拾取到时存在误差,波形并没有完全严格对齐。为了降低人工拾取到时误差,我们采用互相关法计算相对到时对齐波形。采用互相关法计算相对到时时,选取任意两个事件到达同一台站的记录,截取人工拾取P波和S波初至到时前20ms、后100ms的波形,计算两段波形的互相关函数。采用互相关函数最大值对应的时移量对到时差进行校正。图3b显示的是采用校正后的到时差对波形进行对齐后的记录。可以看出,采用互相关法对到时差进行校正后能够更好地对齐波形。

图2 用于微地震定位的初始速度模型

对于该地面微震监测数据,共得到了12557个P波绝对到时,12557个S波绝对到时。基于波形互相关分析,得到了426684个P波相对到时差数据和397601个S波相对到时差数据。我们将这些数据应用于双差地震成像。

图3 基于P波到时的波形对齐效果对比a 利用人工拾取到时进行对齐的波形记录; b 根据互相关到时差进行对齐的波形记录

3 双差地震成像结果

对于速度成像坐标系统,我们选择x坐标轴沿着东西方向,y坐标轴沿着南北方向。双差地震成像算法对模型采用的是网格点表示的方式。根据地震和台站的分布,我们选择的反演网格点在x和y方向上的网格间距是200m,范围为0～2.2km;在深度上z=-1.500,-1.000,-0.500,0,0.250,0.450,0.536,0.650,0.750,0.800,0.950,1.167,1.313,1.550,1.756,1.900,2.156,2.500km。反演采用的初始速度模型如图2所示。

根据双差地震成像法的反演步骤,对人工拾取绝对到时数据、到时差数据、互相关到时差数据采用了分级加权的方法。在反演的第一阶段赋予绝对到时较高的权值,获得较大尺度的地震事件定位结果和速度模型;之后对人工拾取到时差数据赋予更高的权值,来提高地震定位和速度模型的精度。最后对互相关到时差数据加大权值,进一步提高地震定位和速度模型的精度,从而获得精度较高的定位结果和速度模型。图4显示了反演前、后相对走时残差的分布,反演后相对走时残差从原先的19ms下降到1ms,说明数据拟合更好,模型更加准确。

图5和图6分别给出了采用传统网格搜索法和双差速度成像法得到的地震事件定位结果。对比图5和图6可以看出,采用双差地震成像方法得到的震源位置在平面和深度上更加聚集,呈现出更好的线性分布特征,表明该定位结果更加准确。采用传统网格搜索方法定位结果误差较大的原因主要有两方面:一是由于人工拾取到时存在一定误差(图3a),另一方面是由于该方法采用简单的一维速度模型,与实际地层模型存在一定误差。由图5和图6可以看出,压裂产生的微地震主要分布在压裂井的东侧,呈现出非对称分布;在深度上,微地震主要分布在第1压裂段和第3、4压裂段附近,而第2压裂段附近的微地震事件较少。

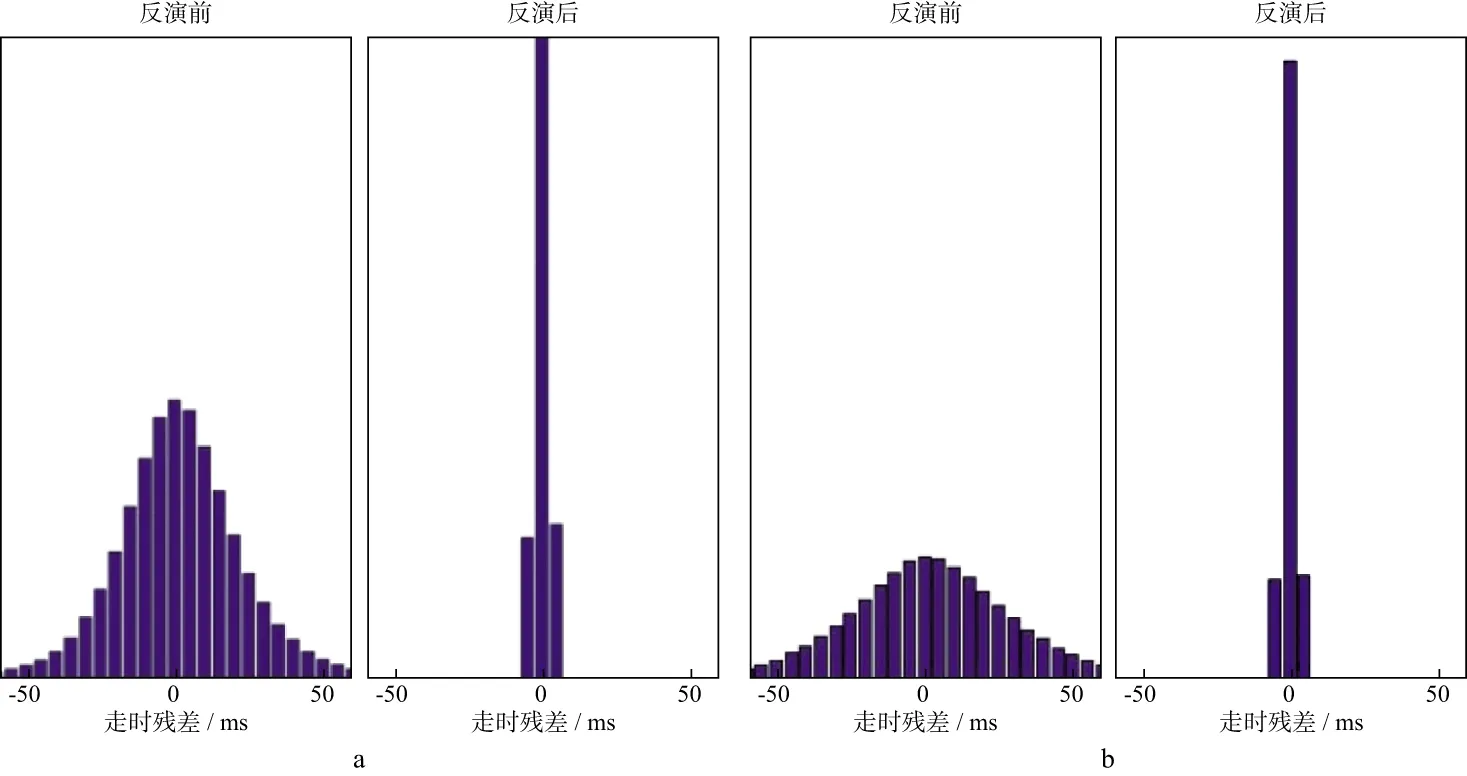
图4 P波(a)和S波(b)反演前、后相对走时残差

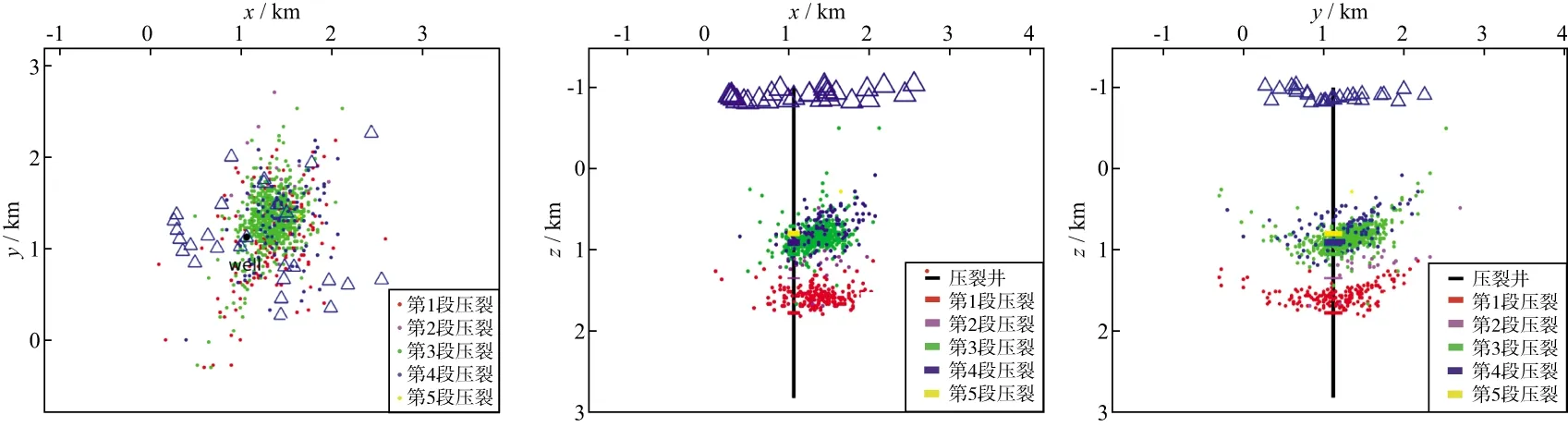
图5 传统网格搜索法定位结果

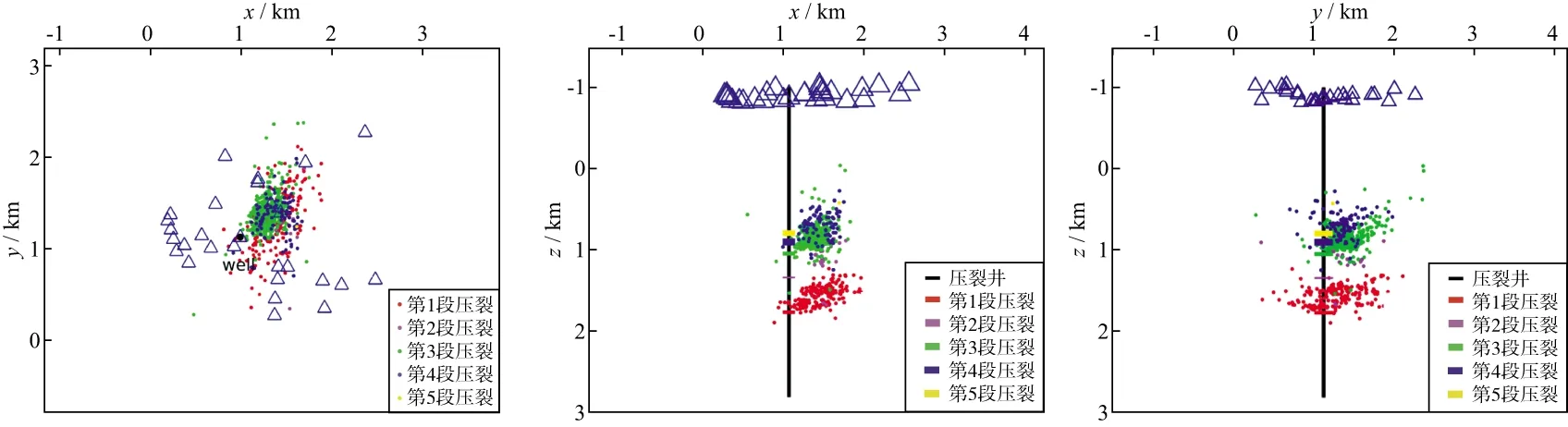
图6 双差速度成像法定位结果

图7和图8分别显示的是反演得到的研究区域内P波和S波在深度0.95km处的速度剖面(水平截面)和对应区域的棋盘分辨率测试结果。棋盘分辨率测试是对三维初始速度模型中的每一个网格点交替±5%的扰动构建棋盘速度模型;采用扰动后的速度模型正演得到理论走时数据,对理论到时添加平均值为0,标准差是2ms的高斯随机噪声;然后利用同样的反演参数对含噪声的正演数据进行反演。若得到黑白分明的相间网格说明该处的分辨率高,反演得到的速度模型可靠。从棋盘分辨率测试结果可以看出,在微地震分布区域,vP和vS模型都有较高的分辨率,与该区域射线分布比较集中有关。图9和图10分别给出了x方向上的vP和vS剖面及其对应的棋盘分辨率测试结果;图11和图12分别给出了y方向上的vP和vS剖面及其对应的棋盘分辨率测试结果。可以看出,在深度上,速度模型也有较高的分辨率。整体来说,浅部(z=0.5～1.2km)的微地震事件分布在低vP和高vS区,深部的微地震事件分布在低vP和低vS区,且浅部的微地震事件个数远多于深部。

图7 深度为0.95km处的vP(a)和vS(b)模型

图8 深度为0.95km处的vP(a)和vS(b)模型对应的棋盘分辨率测试结果

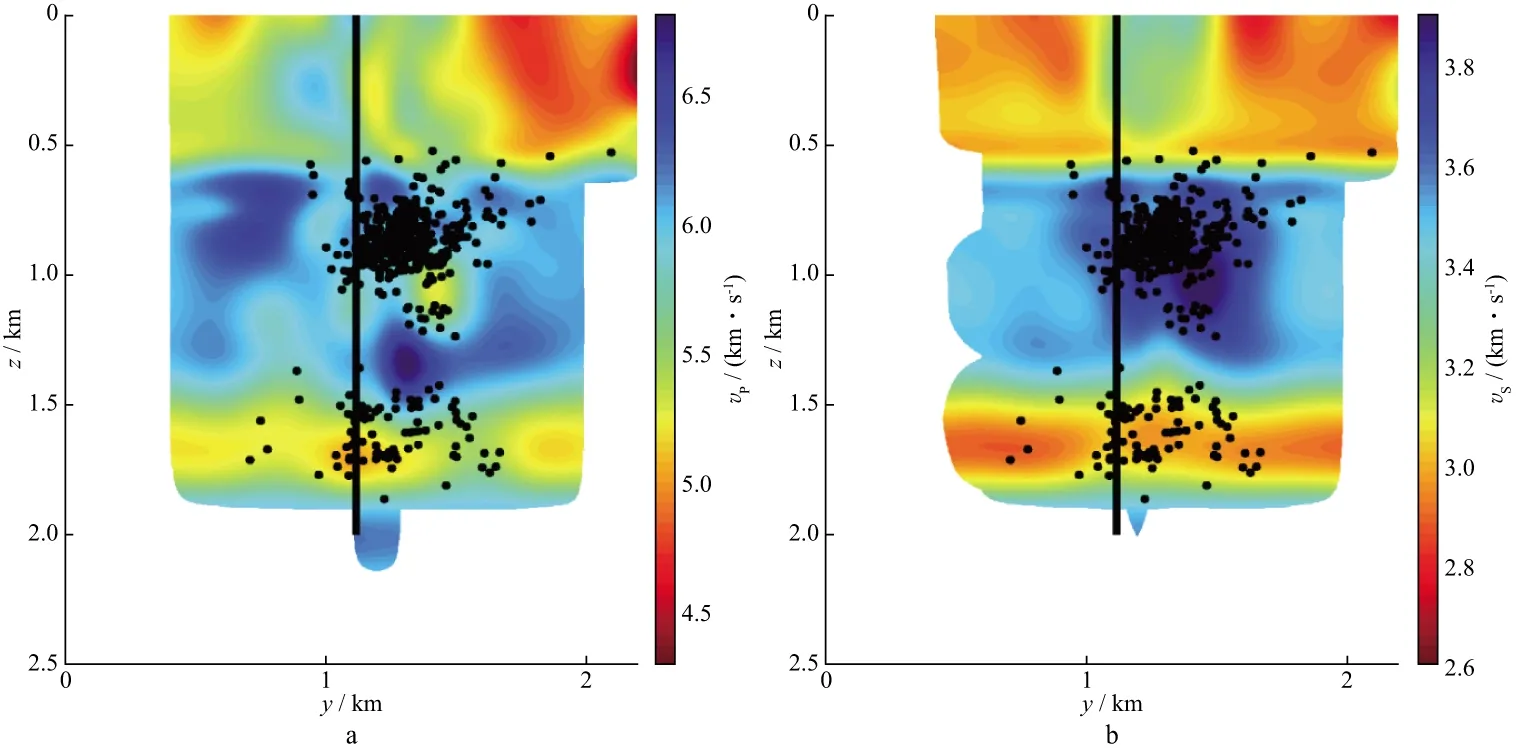
图9 x=1.4km处的vP(a)和vS(b)模型

图10 x=1.4km处的vP(a)和vS(b)模型对应的棋盘分辨率测试结果

图11 y=1.3km处的vP(a)和vS(b)模型

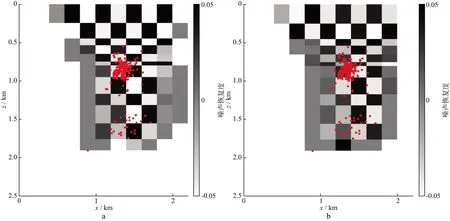
图12 y=1.3km处的vP(a)和vS(b)模型对应的棋盘分辨率测试结果

4 讨论

与大多数井下微地震监测类似,本次地面监测所得到的裂缝相对于压裂井仍然呈非对称分布(图5、图6),尤其是在浅部微地震事件几乎只位于压裂井东侧。与井下微地震监测相比较,地面监测台站的分布相对于压裂井来说几乎对称。因此,微地震事件分布的不对称性并非由观测系统分布的偏差导致。一个可能的原因是压裂井东、西两侧的储层物性存在一定差异,东侧的岩性更容易破裂[35-36];另外一个可能的原因是射孔簇的位置存在一定的偏差而导致压裂液更趋向于朝东侧压裂[37];第3种可能的原因则是压裂井的东侧裂缝较发育而导致东侧更先压开,继而导致裂缝向东侧发育,压裂液向东侧渗流[38]。

对于第1级压裂段,相对压裂井来说微地震事件虽呈现非对称分布,但是在井的两侧均有分布(图5、图6)。微地震事件主要分布在低vP和低vS区(图9至图12)。微地震事件分布在低速异常区域的原因是压裂产生的裂缝以及裂缝中流体的存在导致地震波速度降低[32]。从图7至图12可以看出,浅部的微地震事件主要分布在低vP和高vS异常区域,而且在这个深度区域发生的微地震事件几乎分布在压裂井的东侧。这说明浅部和深部的微地震事件分布区域存在非常明显的区别,意味着这两个深度处的储层物性存在一定程度的差异。岩石物理试验结果显示,由于裂缝的存在会导致P波和S波速度降低[39],但是如果在裂缝区存在气体饱和状态时,S波的速度会上升[40]。根据成像结果可以看出,浅部微地震事件分布在低vP和高vS区域,可以推断在该深度(z=0.5～1.2km)附近,天然裂缝发育而且处于气体饱和状态。由于天然裂缝的发育,在压裂的过程中受到应力扰动,在某些裂缝区域可能会重复诱发较多的微地震事件,就是所谓的重复地震[41],而重复地震的一个特点是波形具有很高的一致性。初步波形分析显示,在该垂直井压裂产生的微地震事件中,存在重复事件。图13显示的是一些记录到的重复地震波形,这些波形具有非常高的相似度,它们之间的互相关系数均大于0.95,这也进一步证明了该深度区域存在大量的裂缝。

图13 检测到的重复地震在垂向分量上的波形

需要强调的是,在水力压裂产生裂缝以及微地震事件的过程中,压裂储层及其附近的速度会随着裂缝的扩展而渐进地发生变化,因此可以利用产生的微地震事件近实时地给出储层附近的速度变化。在本研究中,我们是利用所有压裂段产生的微地震事件综合对压裂目标储层进行速度成像,因此得到的是一个平均意义上的速度变化,反映的是整体上储层由于水力压裂导致的速度变化。

5 结论

本文将双差地震成像方法应用于我国西南地区某页岩气井水力压裂地面微地震监测数据分析。利用拾取的绝对到时数据和采用波形互相关分析得到的到时差数据,可以同时获得高精度的地震定位和震源区速度成像结果。实际数据处理结果表明,与传统网格搜索方法相比,双差地震成像得到的定位精度更高,能够更加准确地刻画裂缝的形态分布。在定位的同时,双差地震成像方法可以确定由于水力压裂导致的储层速度变化情况。在深部,微地震呈非对称分布于压裂井的两侧,并对应于低vP、低vS,该现象是由于压裂产生的裂缝导致地震波速度降低。而在浅部,微地震事件几乎全部分布在压裂井的东侧,并对应低vP、高vS。结合岩石物理实验结果和波形分析,推测该区域天然裂缝发育并且气体饱和。由本研究可知,综合应用微地震事件定位和速度成像结果,可以更加准确地刻画水力压裂对储层的改造效果。