浅谈海上压缩感知地震勘探

黄小刚

(中海油研究总院有限责任公司,北京100028)

2014年,国际油价断崖式下跌,石油公司面临生存考验。地震勘探是油气勘探最主要的手段之一,其支出也是油气勘探的主要部分。地震勘探的复杂化和精细化导致采集数据量急剧增大。随着“两宽一高”(宽频、宽方位、高密度)地震的日益普及,采集、处理成本不断攀升。低油价与采集、处理高成本之间产生了巨大矛盾。海上地震勘探主要成本为地震采集,占总成本的80%以上。因此,在地震采集上进行技术革新的降本增效空间最大。

什么技术能够较为显著地降低地震采集成本,提高采集效率呢？压缩感知技术就是这样一项信号采集、处理的新技术,它被美国科技评论评为2007年十大科技进展之一。该技术理论上不再受限于使用了近百年的经典奈奎斯特采样定律,采用随机、稀疏采样,采集远小于奈奎斯特频率的信号样本即可重建信号[1-2]。地震勘探过程实质就是一个数字信号采集、处理的过程,因而该技术十分适用于地震勘探。早在2011年,马坚伟[3]就提出了利用压缩感知技术降低野外采集数据量,并进行了后续深入研究[4-5];陈生昌等[6]也给出了压缩感知高效地震采集的初步框架;周松等[7]在压缩感知观测系统设计与数据重建方面进行了许多研究,取得了一定进展;CHARLES等[8]和李成博等[9]在压缩感知地震方面进行了较多探索。同样的采集效果,压缩感知采集的成本降为原来的几分之一(减少炮线和接收线),或同样的采集成本可以在保持同样采集质量的情况下采集更大面积的数据,促进增储上产。以2014年为例,我国海上地震采集费用高达数十亿元,若按25%～30%的降本幅度估算,我国每年可因此降本数亿元。因此,压缩感知地震采集的前景十分可观。

但是,观测系统设计较难以及资料的后续处理技术较为缺乏或者不成熟,是压缩感知地震勘探目前没有全面推行的主要影响因素。

压缩感知地震所采集数据量比传统采集要小得多,但并不是可以无限小。压缩感知地震采集需要满足什么条件？如何在现有的采集设备条件下,设计压缩感知观测系统来尽可能满足这些条件？如何评价观测系统的优劣？这些都是压缩感知采集设计必须要研究的课题。

压缩感知地震采集设计、评价、实施和产业化需要配套的处理技术。压缩感知采集的地震资料有别于常规采集资料的规则性和密集性,具有很大的随机性和稀疏性。另外,多震源同时激发技术常被用于压缩感知采集以进一步提高采集效率,但同时震源激发时,炮集混叠现象显著[10],这两个原因导致常规处理方法很难应用于压缩感知地震数据的处理。开展压缩感知地震资料处理关键技术研究,不仅可以为压缩感知采集提供处理技术,而且能指导压缩感知采集设计。

本文首先归纳总结了海上压缩感知地震采集的特点、实施方案、降本增效效果,并采用模型数据验证其应用效果;之后对传统压缩感知地震规则化方法的不足进行了改进,将其应用于模型和实际资料取得了较好应用效果;最后总结了压缩感知同时震源炮集分离、噪声压制等技术的原理和进展。

1 海上压缩感知地震数据采集

压缩感知信号采集的基本思想可以总结为:如果待采集信号在某个域可以稀疏表示(即在该域中非零元素少、零元素多),则该信号可以采用某种随机方式来观测,当观测样本数量满足一定大小时,可采用一定算法较好地重建信号。压缩感知采集涉及三大关键问题[11-12]:①信号能够稀疏表示,其稀疏度决定了压缩感知采样的样本大小,越稀疏,则所需的采样样本越小;②压缩感知观测矩阵是一种随机观测矩阵,其品质可由矩阵的不相干性和受限等距性来表征;③信号的重建问题,通常可采用L1范数代替L0范数来近似表达稀疏约束,从而以阈值迭代的方式来求解一个凸优化问题。

压缩感知的数学理论对观测矩阵要求较高,高斯及伯努利随机观测矩阵理论上能够满足压缩感知采集条件,但施工难度较大。王华忠等[13]认为,只有在独立震源和独立检波器基础上形成的观测系统才能与压缩感知的随机采样方式最佳地结合在一起形成未来的地震数据采集系统。在当前硬件技术尚不满足要求的条件下,不应把精力放在基于压缩感知的随机采样上,而应该放在如何用同时震源激发提高宽方位高密度采集的效率上。显然,现有的地震采集硬件往往较难实现完美的压缩感知采集,因此MOSHER等[14]对压缩感知采集条件做了一定的松弛,采用非均匀最优化采样(NUOS)来进行压缩感知采集设计并且取得了较好的进展。

基于上述考虑,我们给出了海上压缩感知地震采集的基本原则:根据现有采集设备可实现的条件,在能够实现压缩感知随机采样的维度上使用最优化随机观测;在无法实现随机观测的维度上,采用常规观测。例如海底电缆(OBC)观测时,道间距受硬件限制,无法实现最优化随机观测,只能采用传统的观测,但在缆间距上可以实现最优化随机观测。

1.1 海上压缩感知地震数据采集的实现方式

目前海上地震采集接收设备主要有3种:拖缆、OBC和海底节点(OBN)。它们具有不同的特点和灵活度,所以在压缩感知采集的时候,具有不同的实现方式。表1给出了3种接收设备可能的压缩感知采集方式。拖缆采集由于易受海浪、洋流等影响,难以控制接收线距,尤其是大偏移距部分漂移严重,所以在接收线间距方面进行随机优化采集严重受限;OBC采集目前受硬件限制,难以实现道间距的随机优化,但接收线间距可以实现压缩感知随机优化;OBN采集的空间自由度很大,可以实现空间位置的较大随机化,因而能够较好地接近理想压缩感知采集。

表1 海上3种常见采集设备对应的压缩感知采集实现方式

1.2 优化的压缩感知采样方式

理论上,高斯及伯努利随机采样能够满足压缩感知采样要求,但这种完全随机不可避免地会产生一些较大的采样间隔,不利于信号的采集及重建。一些学者研究了优化的压缩感知随机采样方式,如Jitter采样、泊松碟采样以及最远点采样等[15]。

图1给出了3种不同欠采样结果及其对应的频谱[16]。由图1可见,当采用规则欠采样时,频谱上出现了强假频;当采用完全随机欠采样时,频谱上主频突出,假频较弱且分布较均匀,但出现了较大的采样间隔;当采用Jitter采样时,频谱上主频同样突出,假频同样较弱且分布较均匀,没有出现较大采样间隔,有利于信号的重建。因此,相较于完全随机采样,Jitter采样具有较大优势。泊松碟采样及最远点采样也是对完全随机采样的不同优化,具有不同的特点和优势。

1.3 海上压缩感知地震数据采集的降本增效分析

1.3.1 同时震源随机激发

两个及以上震源互不制约地随机激发,能够在相同的时间里采集更多的炮,对于提高采集效率、增加覆盖次数作用显著。

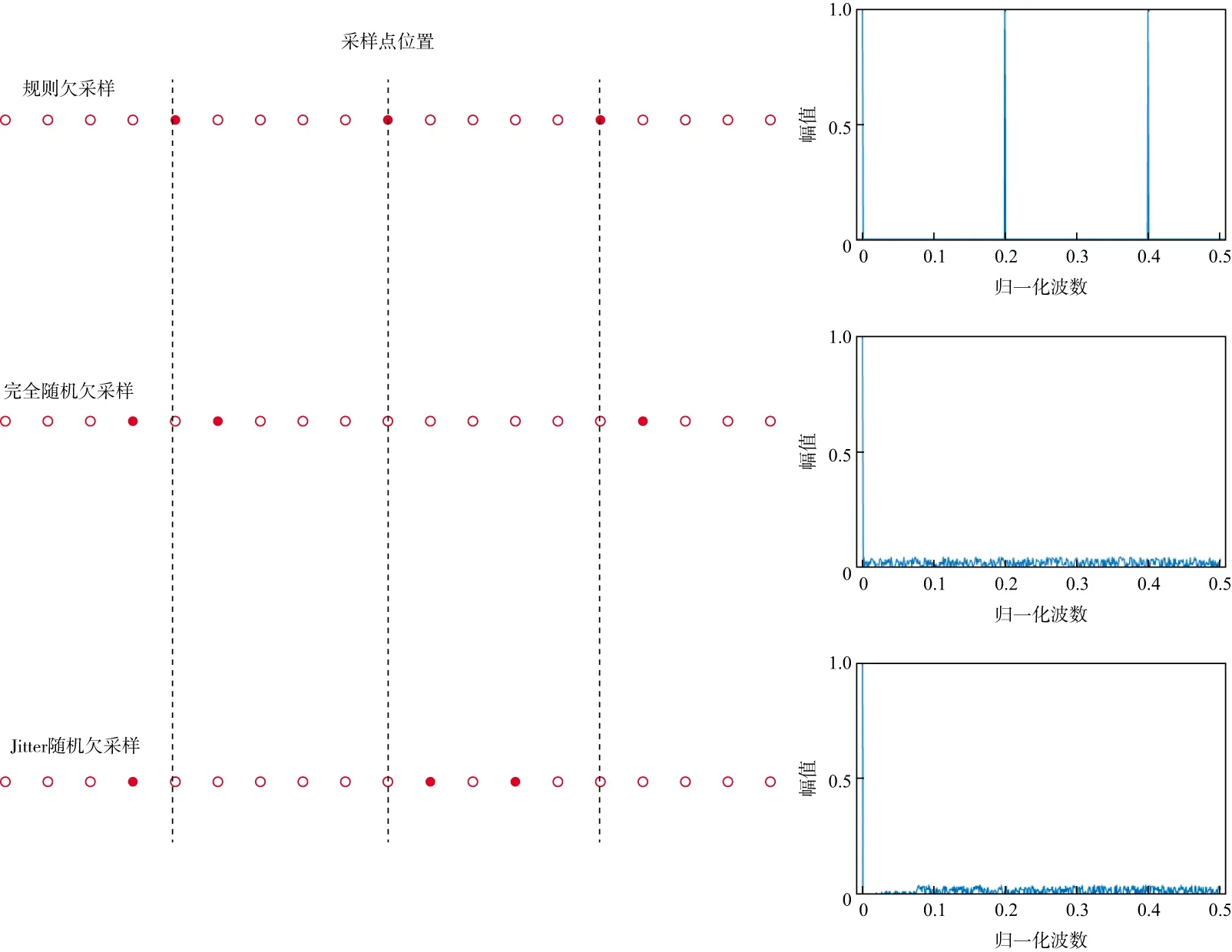
图1 3种不同欠采样结果及其对应的频谱

1.3.2 随机炮间距

不论炮间距大还是小,船都得航行一次,增加炮间距对提高采集效率作用不明显。然而,当采用随机炮间距时,平均炮间距增大,船速受气枪充气时间的限制适当降低,船速可以适当提高,采集效率能够得到一定提升。

1.3.3 随机炮线或检波线(接收线)间距

采用随机炮线间距或接收线间距,可以适度增大平均炮线间距或平均接收线间距,从而在同样采集面积情况下减少炮线或接收线数目,减少炮船的航行次数或布缆工作量,提高采集效率。

1.3.4 随机炮点或接收点空间位置

炮点和接收点空间位置随机,能够接近理想的压缩感知采集。然而在目前的采集设备情况下难以实现炮点空间位置随机。接收点空间位置随机则能够以OBN的形式来近似实现。接收点空间位置随机能够最大限度地减少投放的OBN数目。OBN是一种昂贵的采集方式,压缩感知OBN采集每减少一个OBN点的投放都意味着减少成本。

上述不同压缩感知采集方式具有不同的降本增效效果,将其结合使用时,降本增效效果更佳。“两宽一高”地震勘探优点突出,但其成本高昂。经济、高效的压缩感知地震勘探,使得大规模推行“两宽一高”变得更为可行。

1.4 海上压缩感知地震数据采集观测系统设计和评价方案

观测系统设计与评价需要尽可能利用地下信息,基于地下速度模型,进行高密度地震波场模拟,得到高密度地震数据。考虑施工可行性及压缩感知采集理论,建立初始的压缩感知观测系统,利用该观测系统对模拟的高密度地震数据进行重采样,得到模拟的压缩感知观测数据。利用常规采集观测系统对高密度地震数据进行重采样,得到模拟的常规地震数据。对模拟的压缩感知数据进行规则化处理,并将规则化后的数据与常规数据进行对比。若满足误差要求,则接受此压缩感知观测系统,否则利用误差矩阵对压缩感知观测系统进行优化,直至满足误差要求。

压缩感知观测系统的评价可以通过规则化数据的信噪比、规则化数据与理论数据的误差、观测系统的照明、覆盖次数的均匀性、偏移成像的质量等实现。

上述采集设计和评价方案较为耗时,但其成本相较于地震采集成本而言完全可以接受。对于新探区,地下先验信息往往较为匮乏。在缺少地下先验信息的情况下,假设地下介质为水平层状介质,同样能够进行上述压缩感知观测系统设计和评价。这一思想与常规采集设计、评价类似。实际上,常规采集设计也常常基于此默认假设。

1.5 模型实例

图2a为经典的overthrust三维推覆体模型。为提高高密度正演模拟的效率,降低频散并提高有限差分正演模拟的稳定性,适度地增大了浅层的速度值,减小了中深层的速度值。基于修改后的模型,用OBC的patch观测方式进行了有限差分高密度地震模拟,子波主频为20Hz。共模拟了12个patch的高密度OBC数据(P1～P12),其平面分布如图2b所示。以P4为例,图2b中红色覆盖区为炮点范围,绿色覆盖区为检波点范围。图2c为模拟得到的高密度炮集数据,对模拟的高密度数据进行了常规观测系统重采样和压缩感知观测系统重采样,具体参数如表2所示。压缩感知观测系统设计考虑了现有采集设备的可行性,例如接收线容易实现间距随机,而道间距受OBC硬件限制,无法随机。图2d给出了P4压缩感知观测系统的炮点和检波点以及覆盖次数分布;图2e给出了P4,P5,P6的压缩感知观测系统炮点和检波点以及覆盖次数综合分布。由图2e可以看到,炮点、检波点和覆盖次数分布总体较均匀,但局部存在较大的不均匀性。采用压缩感知规则化可以使之变得更为均匀(图2f)。受正演模拟的高密度观测系统限制,炮线没有采用随机间距,但炮间距和接收线间距均采用了Jitter随机,道间距受硬件限制没有随机。此情况下,采用本压缩感知观测系统,采集的数据量大约为常规采集的2/3。

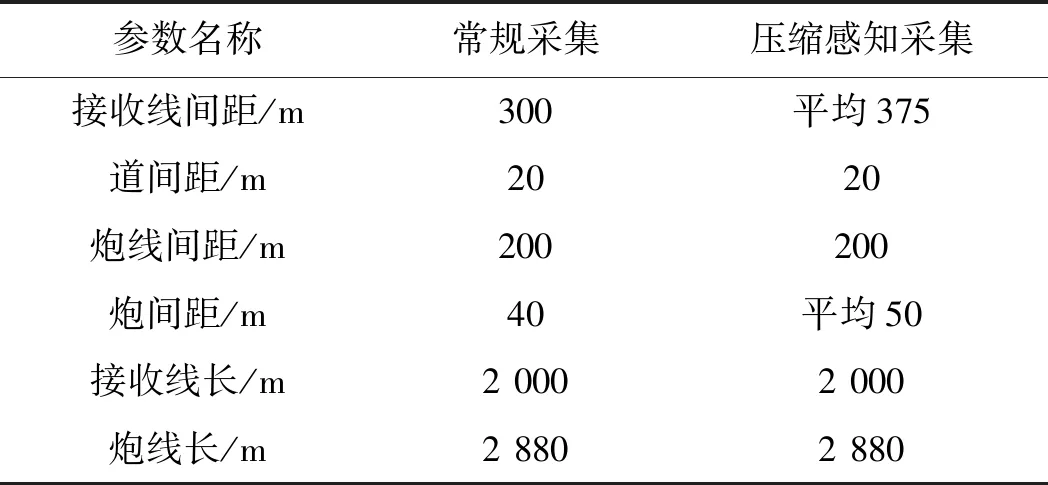
表2 主要采集参数

图3a和图3b分别给出了常规采集数据和压缩感知采集数据规则化后的克希霍夫叠前深度偏移成像结果;图3c为其速度模型剖面。对比图3a和图3b可以发现,除了细微差别外,压缩感知采集数据经过规则化后能够达到与常规采集相当的效果,但减少了1/3的采集数据量。

图2 高密度地震模拟及数据重采样a 三维推覆体速度模型; b OBC采集12个patch的分布范围; c 正演得到的高密度炮集地震数据; d P4的炮点、检波点及覆盖次数分布; e P4,P5,P6炮点、检波点及覆盖次数分布; f P4,P5,P6规则化后的炮点、检波点及覆盖次数分布

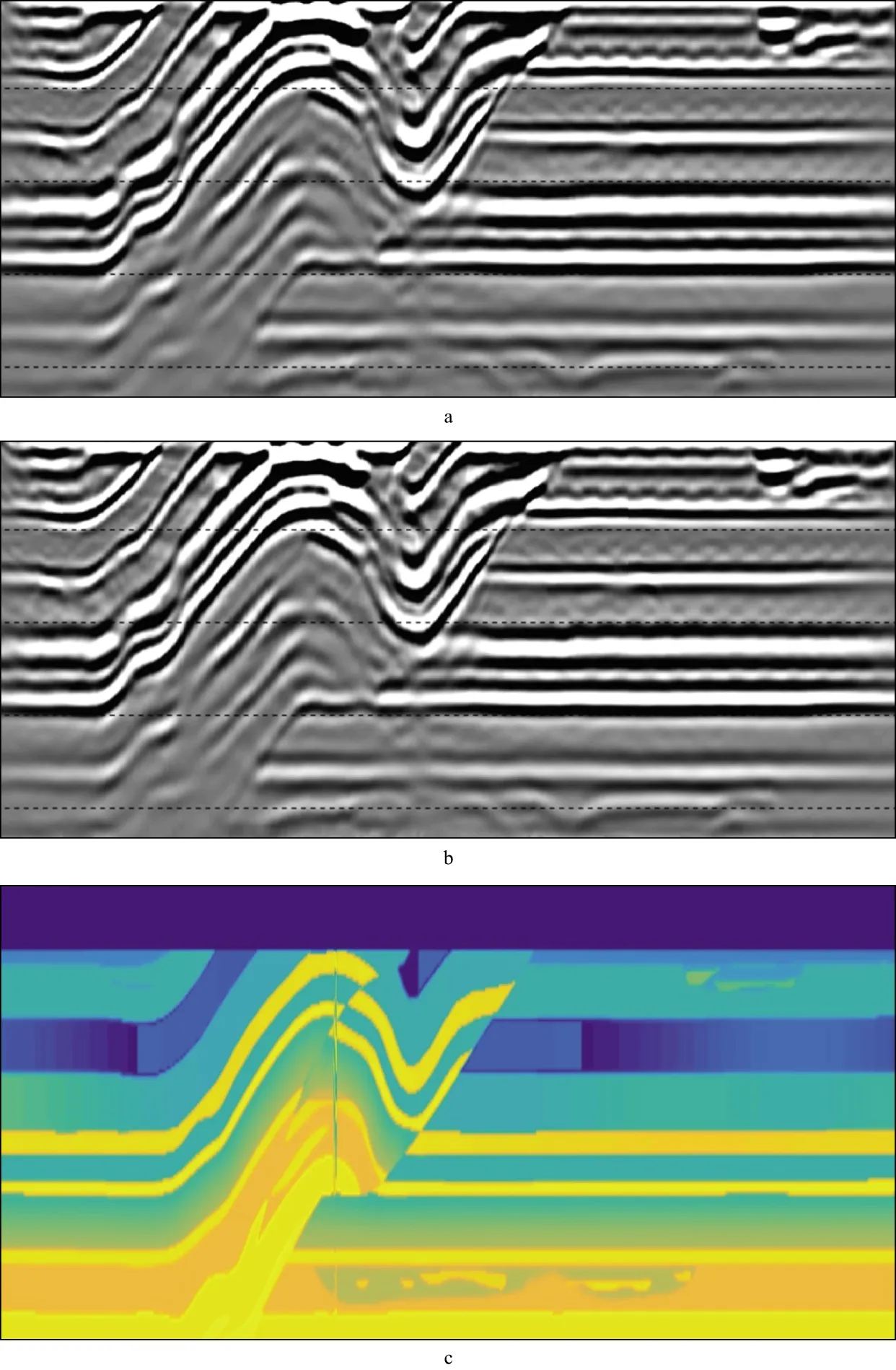
图3 常规采集与压缩感知采集的成像结果(Inline 300)a 常规采集数据成像剖面; b 压缩感知采集数据规则化后的成像剖面; c 速度模型剖面

2 海上压缩感知地震数据处理

除了用于地震数据采集外,压缩感知技术在地震资料处理中也有较大的应用空间,主要用于改善处理效果或提高处理效率。其中,压缩感知地震数据规则化是与压缩感知地震数据采集设计紧密相关的一项处理技术,它不仅搭起了压缩感知地震数据采集与后续常规处理间的桥梁,更为压缩感知地震数据采集设计提供了一种评价手段。

2.1 基于压缩感知的地震数据规则化

导致地震数据采集观测系统不规则的因素很多。例如,压缩感知采集的地震数据具有天然的不规则性。另外,由于钻井平台等障碍物的存在,潮汐、洋流等的影响,导致地震数据炮点、检波点分布也不规则。这种数据不规则对后续处理有较大影响,如果不进行规则化就很难用传统的处理方法进行处理。地震数据不规则对偏移成像、多次波压制等也有较为显著的影响[17]。

无论是压缩感知采集的数据还是常规采集数据,地震道往往不是严格地分布在规则网格上。要实现其规则化,通常有两种思路:一是采用适应非规则网格的运算,输出规则网格地震道(输入图4a地震道,运算后直接输出图4b结果)[18];二是应用插值实现规则化,即加密地震道(图4c),对地震道执行bin处理,采用规则网格的运算,输出目标规则网格地震道(如输入图4a地震道,经过图4c处理,运算后输出图4b 结果)。前者无法使用快速傅里叶变换(FFT),效率较低;后者地震道虽然增加,但可以使用FFT,效率高。

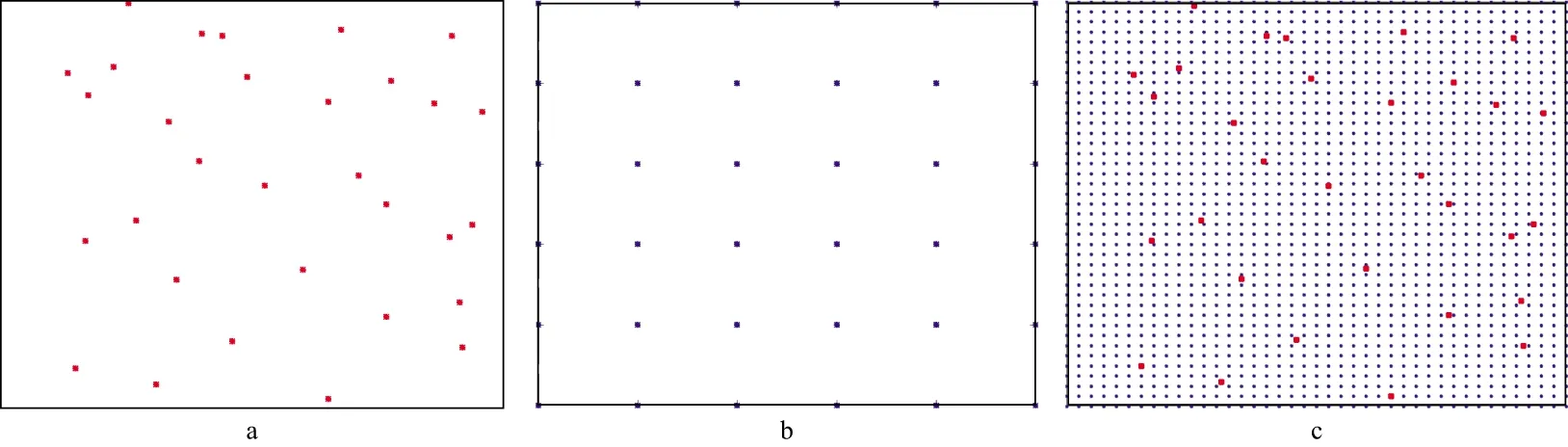
图4 压缩感知数据规则化思路a 不规则地震数据炮点或接收点分布; b 规则化输出的地震数据炮点或接收点分布; c 加密后的地震数据炮点或接收点分布

ABMA等[19]将压缩感知思想引入数据规则化领域,采用阈值迭代和稀疏反演来实现数据规则化,具有较高的计算效率,并且处理随机缺失数据效果很好,因而尤其适用于压缩感知采集的地震数据。该方法能够较好地压制随机缺失引起的非规则假频,但压制由规则缺失引起的规则强假频较为困难。而实际数据往往是随机缺失与规则缺失的叠加,因而处理较为困难。

针对上述问题,对变换域数据进行加权处理,使其能在压制随机缺失导致的随机假频的同时,也能较好地压制规则缺失引起的规则强假频。

传统压缩感知地震数据规则化方法阈值迭代求解公式[20]为:

(1)

对上述传统方法变换域的数据进行了适当的加权处理,总体思想是沿着真实频谱方向权值较大,而其它方向权值较小。修改后的迭代公式为:

(2)

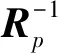
2.2 基于压缩感知的同时震源炮集分离

同时震源随机激发技术能够显著提升地震数据采集效率,但它面临混叠炮集的分离问题[10]。在炮域,干扰炮表现为规则干扰,但是在共接收点域或共偏移距域,干扰炮就类似于随机噪声[21-24]。常规处理可以使用滤波方法来压制它源干扰,但效果欠佳。一些学者应用反演策略实现同时震源的炮集分离[25-29],WASON等[30-31]将压缩感知及稀疏反演应用到同时震源的炮集分离,分离精度较好。周艳辉等[32]将机器学习与稀疏反演相结合进行同时震源的炮集分离,进一步提高了分离的精度。

基于压缩感知和稀疏反演的同时震源炮集分离的基本原理是:对于共接收点道集,假设其在某个变换域的信号稀疏,则可以用L1范数代替L0范数,建立该稀疏约束下的目标函数:

(3)

式中:d是一个检波点接收的同时震源数据;m是待恢复的无干扰炮数据;A是混叠算子,即由无干扰炮数据m生成d的算子;C是稀疏变换算子;λ是拉格朗日乘子。这是一个凸优化问题,可用类似于压缩感知规则化的求解方式进行阈值迭代求解。

2.3 基于压缩感知的地震数据噪声压制

地震数据噪声压制是地震资料处理中的一个重要环节。压噪的方法多种多样,各有其适应性。对于随机噪声而言,使用压缩感知和稀疏反演是一种有效手段。HERRMANN等[33]、NEELAMANI等[34]和HENNENFENT等[35]将曲波变换应用于压缩感知压噪,取得了较好的压噪效果;为了避免人工调节迭代过程中的阈值,曹静杰等[36]提出了一种自适应调节阈值的压噪方法。基于曲波变换的压缩感知去噪方法在去除噪声的同时使信号边缘产生了不光滑畸变,且对有效信号有损伤,因而唐刚[15]、刘伟等[37]提出一种基于压缩感知和全变差准则约束的压噪方法,取得了更好的压噪效果;南方舟等[38]提出一种基于阈值迭代和改进的冷却阈值法的压缩感知压噪方法,并将其应用于海底地震仪(OBS)数据的噪声压制;唐刚[15]将字典学习与压缩感知压噪相结合,依据地震数据特征自适应地变换稀疏变换基函数,从而取得了较好的压噪效果。

压缩感知地震数据噪声压制的基本假设是信号在变换域稀疏。基于这一稀疏假设,可以建立压缩感知噪声压制的目标函数[15,36]:

(4)

式中:y是含噪数据;x是稀疏变换域的系数;CT是稀疏逆变换算子。该问题同样是个凸优化问题,可用阈值迭代法进行求解:

(5)

式中:i表示第i次迭代;Ti是第i次迭代时的阈值。

2.4 压缩感知处理技术的应用

2.4.1 压缩感知数据规则化的应用

1) 模型数据应用。图5a给出了隔道缺失的地震数据采用传统压缩感知方法得到的规则化处理结果;图5b为其对应的频率-波数谱。由图5a和图5b可见,由于规则强假频的存在,迭代过程难以分辨真假频谱,因而重建失败。利用改进后的方法进行规则化处理,得到的结果如图5c所示;图5d为其频率-波数谱。由图5c和图5d可见,改进后的方法能够对规则缺失道进行较好的重建,压制假频。事实上,改进后的方法对于既存在随机缺失又存在规则缺失的数据也有较好的适应性,因此,该方法对于压缩感知采集数据及常规采集数据均适用。

2) 规则化仿真的压缩感知采集数据。图6a给出了真实炮集经过压缩感知重采样得到的仿真压缩感知采集数据。数据缺失道为规则缺失叠加随机缺失,因而其频率-波数谱(f-k谱)(图6b)不仅存在随机假频,还存在规则强假频。采用谱加权压缩感知规则化处理后的数据如图6c所示,其f-k谱如图6d所示。由图6c和图6d可见,随机缺失和规则缺失的道都得到了较好的重建,两种假频也均得到了较好压制。

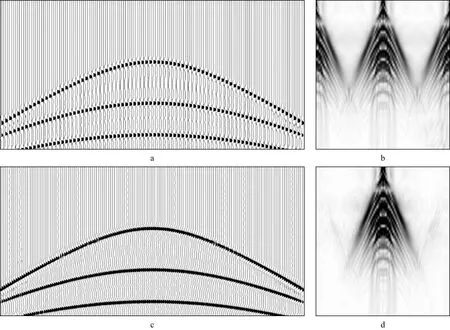
图5 隔道缺失地震数据采用改进前、后压缩感知方法得到的规则化处理结果a 采用传统压缩感知方法得到的规则化处理结果; b 图5a对应的频率-波数谱; c 采用改进方法得到的规则化处理结果; d 图5c对应的频率-波数谱

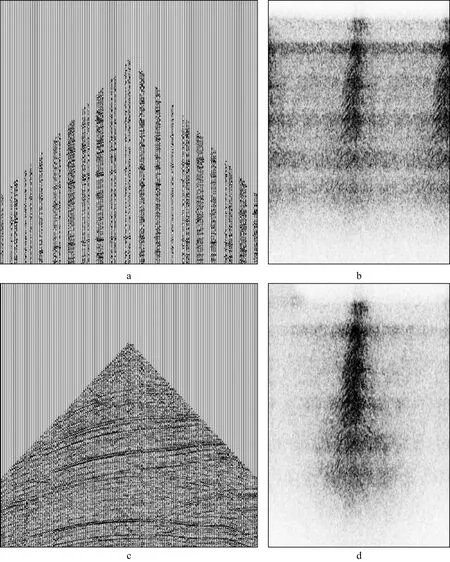
图6 仿真压缩感知数据规则化处理结果a 仿真的压缩感知采集数据; b 图6a对应的f-k谱; c 改进方法得到的规则化处理结果; d 图6c对应的f-k谱

3) 重建缺失炮。实际地震数据有时存在缺炮现象,如图7a所示,缺失左边一炮,在炮域无法将其重建。当数据分选为其它道集时(如共偏移距道集),缺失炮就变成了一些缺失道(图7b)。采用谱加权的压缩感知规则化方法进行处理,得到的道集数据如图7c 所示,可见,缺失道都得到了较好重建。将重建后的道集分选回炮域,得到如图7d所示结果。重建炮(图7d左边)与邻近炮(图7d右边)非常相似,说明该方法对于缺失炮有良好的重建效果。

4) 提高OBN时移地震可重复性。时移地震是油藏监测的重要手段,它需要前、后两次地震采集、处理尽可能保持一致,从而将差异归因于油藏本身的变化。中国海油某油田采用OBN进行了时移地震监测。OBN采集成本非常高,因而道间距往往较大。基数据采集已完成,OBN道间距为150m。为降低成本,需评估增加OBN道间距对时移地震可重复性的影响以及规则化对提高时移地震可重复性的作用。基于该油田的地下速度模型,正演模拟了150m和300m道间距的OBN地震数据。时移地震处理结果表明,300m道间距数据对基数据的时移地震可重复性不理想。图8a给出了300m道间距的OBN炮集数据。因道间距过大,要在炮域将其加密为150m的道间距,必然带来较大的误差。与拖缆不同,OBN可将其变换到共偏移距域进行插值,加密地震道。图8b 给出了其共偏移距道集。利用谱加权的压缩感知规则化处理方法在共偏移距道集上对其进行插值,将其道间距变为150m,结果如图8c所示。由图8c可见,在共偏移距域,尽管道间距很大,每两道间缺失很多道,但同相轴平直,因而可以得到较好的重建结果。图8d 是将重建结果变换回炮域的结果。由图8可见,谱加权的压缩感知规则化方法对OBN数据有较好的插值效果,因而能够提高时移地震可重复性,使其平均归一化均方根振幅值(Normalized Root-mean-square,NRMS)由0.1478降至0.1043。

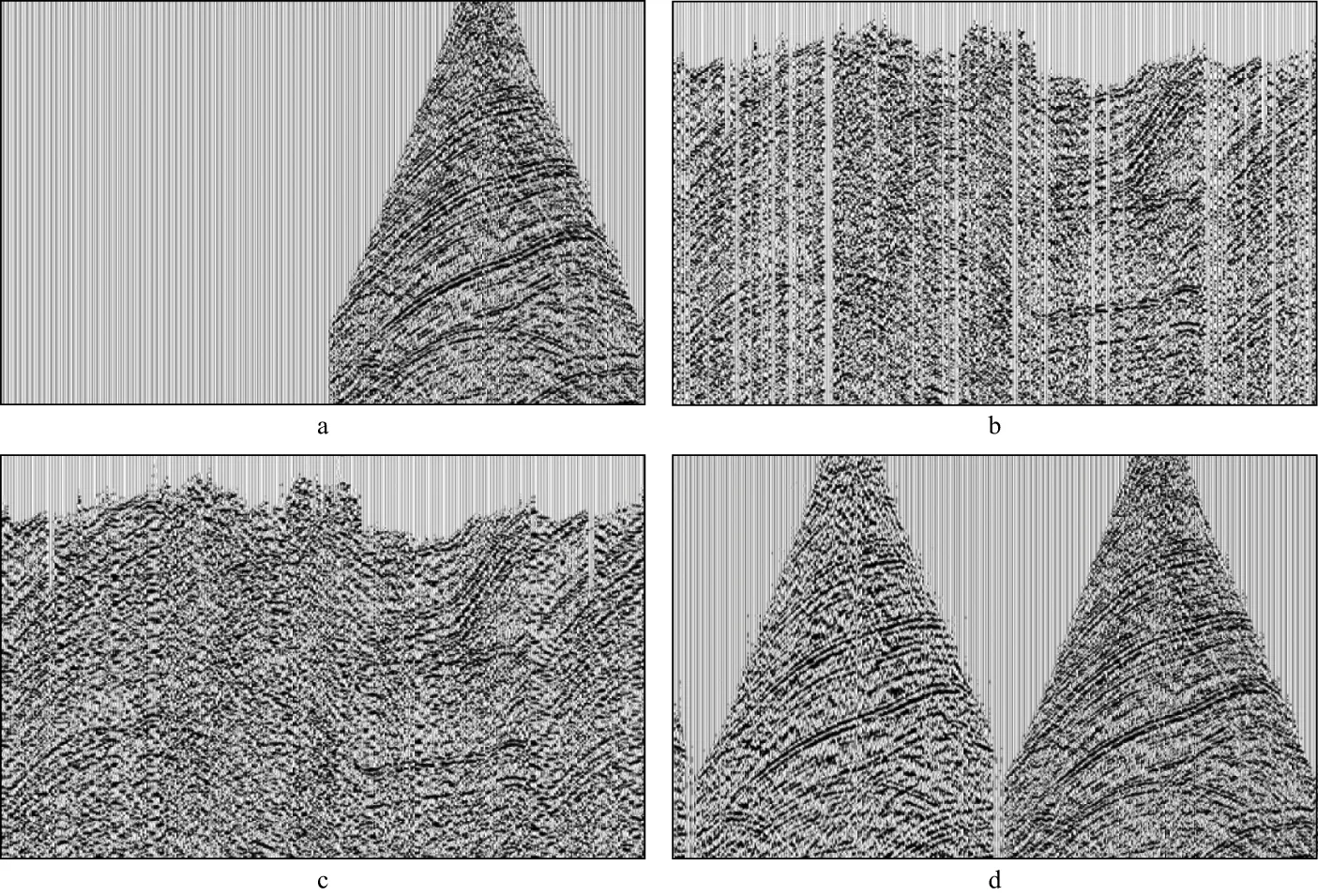
图7 缺失炮重建结果a 含缺失炮的炮集数据; b 图7a对应的共偏移距道集; c 采用改进方法对图7b进行规则化处理后的结果; d 将图7c分选回炮域的结果

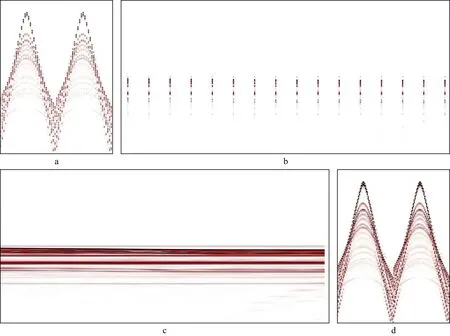
图8 改进方法加密OBN数据的结果a 300m道间距的OBN炮集数据; b 图8a的共偏移距道集数据; c 采用改进方法将图8b插值到150m 道间距的结果; d 图8c变换到炮域的结果

5) 改善偏移成像质量。数据规则化能够压制偏移划弧等假象、改善偏移成像质量。图9a给出了某三维工区共偏移距向量片(common offset vector tile,COV)道集切片。利用谱加权的压缩感知规则化方法对COV道集进行了规则化处理,得到处理后的COV道集切片如图9b所示。可以看到,规则化处理后原来的缺失道得到了较好的重建。对规则化处理前、后的数据进行偏移成像,得到的结果如图10a 和图10b所示。由图10a和图10b可见,规则化处理前,COV道集中存在许多缺失道,影响了偏移成像质量,偏移成像剖面上存在严重的偏移划弧现象;规则化处理后,偏移划弧等假象得到了有效压制,偏移成像质量得到了显著提高。

图9 采用改进的规则化方法对某三维工区地震数据进行规则化处理前(a)、后(b)的COV道集切片

图10 采用改进的规则化方法对某三维工区地震数据进行规则化处理前(a)、后(b)的偏移成像剖面

2.4.2 压缩感知压噪的应用

图11给出了某实际单炮的压缩感知压噪结果。图11a为含噪的单炮记录;图11b为采用基于压缩感知和曲波变换的压噪方法处理后的单炮记录;图11c为去除的随机噪声。从图11中可以看到,采用压缩感知压噪方法,随机噪声得到了较好的压制。

图11 某实际单炮的压缩感知压噪结果a 含噪的单炮记录; b 压缩感知压噪后的单炮记录; c 去除的噪声

3 未来发展方向展望

压缩感知技术正在引发地震勘探革命,它将深远地改变地震采集、处理、解释的面貌。海上压缩感知地震勘探的主要发展方向将体现在以下几个方面。

1) 压缩感知地震高效、经济采集。采集成本是地震勘探成本的主体,采集方面降本增效的潜力最大。压缩感知高效、经济采集始终是压缩感知地震勘探发展的最主要方向,并且它将与“两宽一高”采集相结合,实现高效、经济的“两宽一高”地震采集。压缩感知高效、经济采集的发展方向之一是利用现有采集设备,优化压缩感知采集观测系统,实现采集的降本增效;发展方向之二是促使采集硬件的更新换代,设计生产出更适合海上压缩感知地震采集的设备,例如推进OBN的常规化,生产出道间距可调的OBC,研制出空间位置控制更灵活的海面检波器等。

2) 压缩感知优质、高效处理。基于压缩感知理论,许多常规的地震处理环节都能够得以提速或改善效果。压缩感知技术能够加速波动方程偏移速度分析(WEMVA)、全波形反演(FWI)、偏移成像等计算密集型处理环节[39-40],也能够用于叠后地震数据的提高分辨率处理等。另外,不经过数据规则化,实现压缩感知数据的直接偏移成像也是压缩感知地震处理的一个重要发展方向。

3) 压缩感知海上油藏地震监测。在油气开发阶段,海上时移地震是重要的油藏监测手段。常规时移地震对基数据和监测数据的采集一致性有严格要求。压缩感知时移地震不仅能够显著降低时移地震采集的成本,更提供了一种松弛前、后两次地震采集一致性要求的可能性[41],具有巨大的潜在价值。

4 结论与认识

本文较系统地归纳总结了压缩感知技术在海上地震勘探中的初步应用情况。压缩感知地震勘探基于压缩感知理论,具有显著的稀疏性和随机性。该技术能够应用于海上地震采集、地震处理以及油藏监测等海上地震技术中。

将压缩感知技术应用于海上地震采集时,在保持相同采集质量的前提下,采集的工作量和数据量将显著小于常规地震采集;设计了OBC压缩感知观测系统,对正演模拟的高密度地震数据进行重采样,得到模拟的海上压缩感知数据,在减少1/3采集数据量的情况下,取得了与常规采集相当的处理效果,展现了压缩感知采集的良好效果。今后应加强压缩感知采集与昂贵的海上“两宽一高”地震的结合,使其尽可能地服务于日趋复杂的海上地震勘探;还应加强海上压缩感知地震采集的仪器设备、配套控制软件的研发升级,使得压缩感知地震勘探在海上变得更为灵活、可行。

将压缩感知技术应用于地震资料处理时,一方面可以将压缩感知采集的数据规则化,为后续的常规处理奠定基础;另一方面可以用于同时震源炮集分离、噪声压制、提高分辨率等改善效果的处理,也能用于提速FWI、偏移成像等计算密集型的处理环节。压缩感知数据规则化是一项承接压缩感知采集和处理的关键处理技术。基于谱加权的压缩感知数据规则化方法扩展了传统方法的适应性,模型和实际数据的应用效果展现了其有效性和实用性。目前许多基于压缩感知的处理技术尚处于理论研究阶段,今后应加强压缩感知处理技术的实用化研究,使其在生产中提升处理效率,改善处理效果。

压缩感知技术还能用于开发地震进行油藏监测,降低时移地震成本,松弛时移地震前、后两次采集的一致性要求。今后应加强时移地震采集与压缩感知采集技术的结合,使得压缩感知技术在昂贵的时移地震中发挥降本增效作用。

压缩感知作为一项前沿技术,在海上地震勘探中的应用前景已经充分体现。但该技术还刚起步,尚不成熟,要使得该技术实用化,还需进行一系列的攻关。