基于波动方程转换的时间域多尺度全波形反演速度建模

何兵红,方伍宝,刘定进,胡光辉

(1.中国石油化工股份有限公司石油物探技术研究院,江苏南京211103;2中国石油大学(北京),北京102249)

近年来,基于波动理论的全波形反演技术在深度域速度建模中发挥了重要作用,且在海洋资料处理中得到了成功应用[1-3]。但由于全波形反演强烈依赖于初始速度模型和低频地震数据,需要采用合理的反演策略来减少周波跳跃影响,防止反演陷入局部极值。频率域全波形反演可以实现从低频到高频的多尺度全波形反演,利于提高全波形反演的稳定性[4],但频率域正演计算量大、内存需求高,且需要求解矩阵方程,不适用于大规模地震数据的计算。时间域地震正演计算效率高,但不利于实现多尺度反演。SIRGUE等[5]提出了时间域正演、频率域反演的混合域全波形反演方法,充分利用了时间域正演和频率域多尺度反演的优势,但频率域反演需要谨慎选择合适的反演频率以避免出现吉普斯现象,同时,混合域全波形反演的每一次迭代需要将地震数据从时间域变换到频率域,对于大规模实际资料反演,计算量的增加不可忽视。为了实现时间域从低波数到高波数的全波形反演,一些学者通过包络反演实现低波数速度构建[6-8],在包络反演的基础上开展中高波数速度反演[9-13],形成了以包络反演为核心的一系列多尺度全波形反演方法[14-15],但实际地震数据包络的计算具有多解性。

针对时间域难以开展多尺度反演的问题,本文根据不同参数化模式下的声波方程敏感核函数和辐射模式特征,提出了一种基于时间域波动方程转换的多尺度全波形反演方法,完全在时间域进行波场模拟和反演,通过转换全波形反演参数化模式及其波动方程,实现速度模型从低波数到高波数的多尺度反演。最后通过MarmousiⅡ模型数据的测试验证了方法的有效性。

1 基于阻抗-速度波动方程的低波数速度反演

在不同的参数化模式下,波场扰动对各参数扰动的敏感度不同,敏感核函数则是连接波场扰动和参数扰动的桥梁和关键。GHOLAMI等[16]研究了垂直各向异性介质中拟声波方程的参数化模式以及敏感核函数。PRIEUX等[17]和OPERTO等[18]探讨了多分量地震数据的参数化模式。本文为了实用化,仅探讨声波方程多参数全波形反演问题。声学近似条件下,地球介质的表征参数通常包括速度、密度、阻抗、体积模量等。阻抗-速度参数化模式下速度和阻抗的敏感核函数分别为[19]:

式中:ω表示角频率,ρ表示介质密度,v表示速度,P0(x,ω)是背景波场,G0(r,ω;x)为格林函数。速度敏感核函数KIPv-v(x)表示地球介质用阻抗和速度表征时速度的相对变化量产生的扰动波场的强度。同理,阻抗敏感核函数KIPv-IP(x)表示在相同的阻抗-速度参数化模式下阻抗的相对变化量产生的扰动波场的强度。

对应的阻抗-速度辐射模式表示为[20]:

(3)

图1为阻抗-速度模式辐射图,从速度的辐射特征(红色)可以看出,速度扰动主要产生了大角度扰动波场。相应的,对于地震反问题,在阻抗-速度参数化模式下,大角度(远偏移距)地震数据反演主要得到速度更新量。由于偏移距越大低频信息越丰富,反演结果中大尺度低波数成分越能得以恢复,因此,我们首先采用阻抗-速度参数化模式建立相应的阻抗-速度波动方程,并开展波动方程地震波场数值模拟,为实现全波形反演低波数速度构建奠定基础。

图1 阻抗-速度模式辐射特征(红色代表速度,蓝色表示阻抗,0～360°代表散射角度,半径表示扰动波场强度)

根据波阻抗与速度、密度的关系,建立了基于声波假设的一阶阻抗-速度方程:

(4)

式中:p为压力场,IP为纵波阻抗,vP为地震波传播的纵波速度。vx、vy、vz为x、y、z三个方向的质点振动速度。为了消除地震波数值模拟中模型空间有限引起的边界反射,本文采用了不分裂卷积完全匹配层吸收边界条件(CPML)[21],得到了基于CPML边界条件的阻抗-速度方程:

(5)

式中,φi表示在i(i=x,y,z)方向的递归函数:

(6)

式中:χi、di和αi表示在i方向的阻尼系数;n代表迭代次数。

利用方程(5)可以实现地震波场的波动方程数据模拟。为了将模拟数据与观测数据进行匹配,本文根据模拟数据和观测数据的波场误差2范数形式建立相应的目标泛函:

(7)

式中:RF[IP,vP]表示检波点处接收到的模拟波场;dobs为观测数据。

采用伴随状态法可以得到阻抗-速度模式下的速度更新梯度:

(8)

式中:DFv[IP,vP]表示阻抗-速度方程(5)对阻抗的一阶偏导数;q为伴随波场,是波场误差的反传波场;符号〈,〉表示内积。

将方程(5)加入震源项f并表示为矩阵形式:

(9)

其中,

(10)

(11)

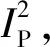
(12)

同时,将震源项转化为:

(13)

得到伪保守的波动方程:

(14)

因而在计算伴随波场q时可以采用与正演算子相同的数值求解形式,以降低计算量。

2 基于速度-密度波动方程的高波数速度反演

声波方程中速度-密度参数化模式下的速度和密度敏感核函数为[19]:

对应的速度-密度辐射模式可以表示为:

(17)

图2为速度-密度模式辐射图。可以看出,当初始速度模型不准确时,常规的速度-密度方程反演利用了大角度和小角度地震数据同时获得了低波数和高波数速度,不利于开展多尺度时间域全波形反演。当初始速度模型中已经包含丰富的低波数成分时,采用速度-密度方程进行全波形反演则主要得到高波数速度成分。

本文采用自伴随的速度-密度一阶速度-应力方程进行波场模拟:

(18)

采用CPML边界条件,得到如下自伴随方程:

(19)

由于基于速度-密度的全波形反演方法已经被广泛熟知[23-24],本文在此不再赘述。

综上所述,首先通过阻抗-速度模式拟合波场误差中远偏移距地震数据,反演得到大尺度低波数速度成分,然后利用速度-密度模式拟合近偏移距地震数据,反演小尺度高波数速度成分,从而在不增加计算步骤和计算量的情况下,实现多尺度速度模型的构建。

3 模型测试

利用MarmousiⅡ模型对本文方法进行了验证。为了提高计算效率,对原始MarmousiⅡ模型进行了重采样,深度方向和测线方向均采用10m采样间隔,炮点(131炮)和检波点(1300个检波器)均匀分布于地表。图3为真实速度模型,图4为初始速度模型。采用常规的速度-密度方程进行全波形反演速度构建时,第一次迭代的梯度中既包含低波数成分,又包含高波数成分(图5)。由于初始速度缺失低波数成分,以此为背景得到的高波数速度成分实质上与真实的高波数成分存在相位不一致的问题。即当初始速度不够准确时,直接采用常规的速度-密度方程进行低波数和高波数同时反演将导致高波数反演产生严重的周波跳跃现象(图6)。从图6还可以看出,在MarmousiⅡ模型CDP400～CDP700、深度1000～2000m范围内断层发育、构造复杂的区域,反演得到的速度结构杂乱,严重偏离真实构造特征。

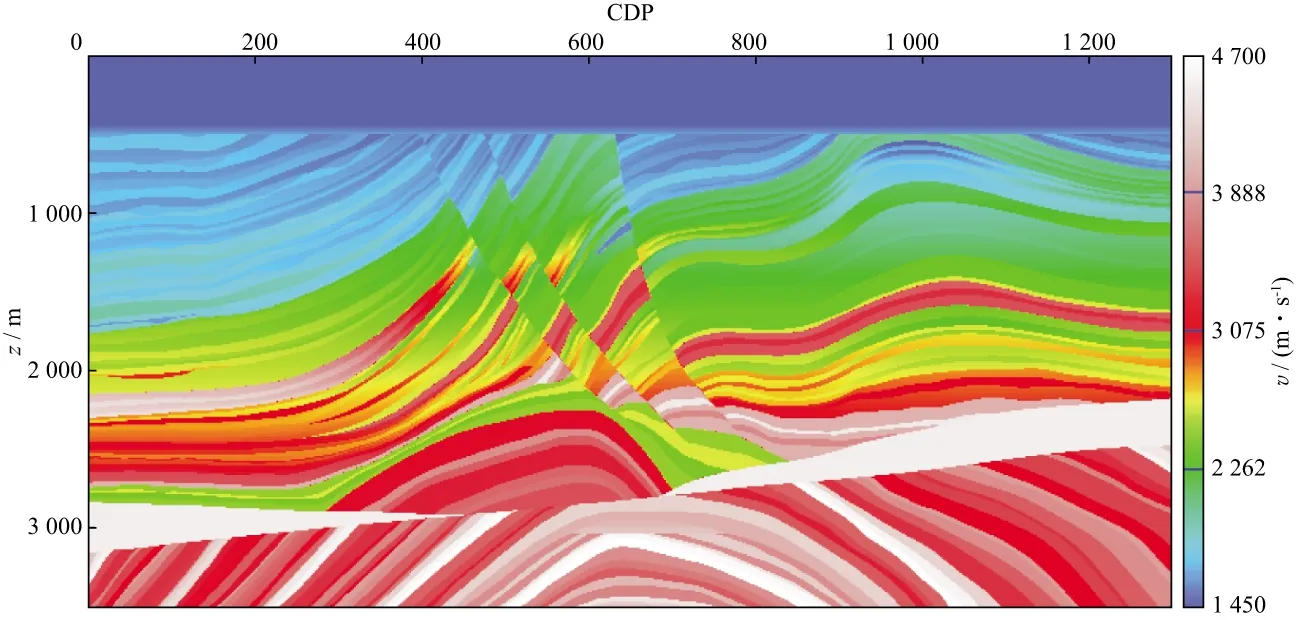
图3 MarmousiⅡ真实速度模型

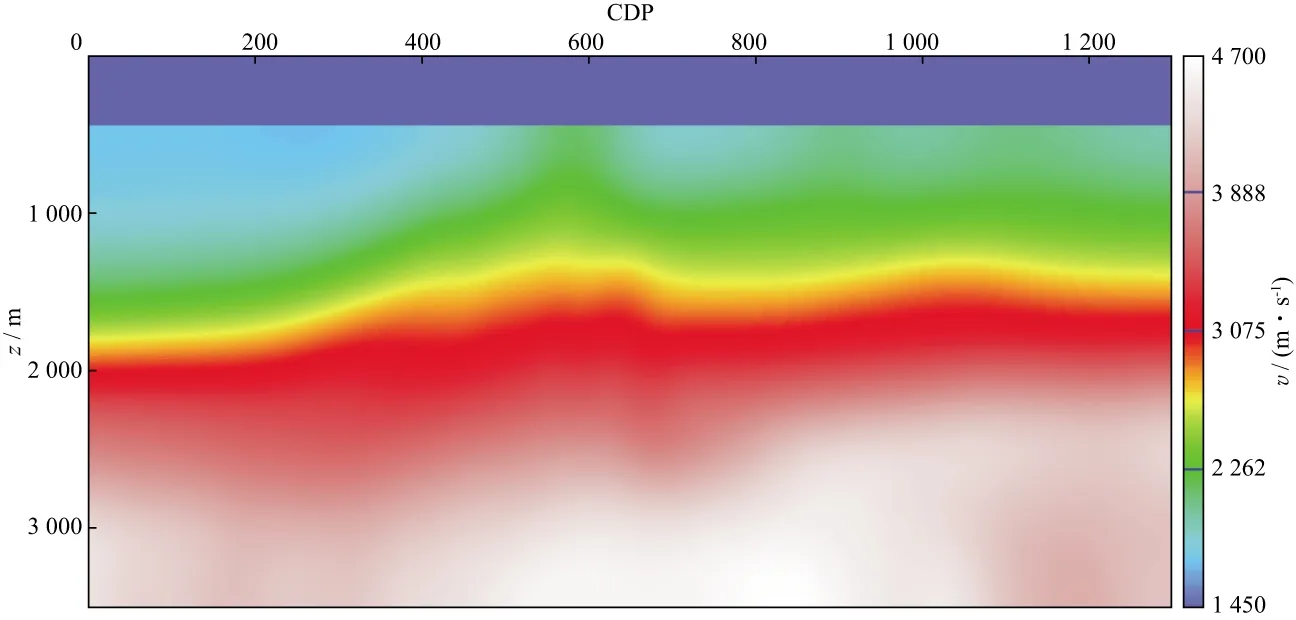
图4 MarmousiⅡ初始速度模型

图5 直接进行速度-密度模式全波形反演的速度梯度

为了验证从低波数到高波数的多尺度反演是减少周波跳跃现象、正确反演地下构造特征的有效手段,本文通过阻抗-速度模式的全波形反演得到低波数的速度更新梯度(图7)。图8是速度-密度模式和阻抗-速度模式的全波形反演速度梯度的差异,可以明显看出两者的差异主要在于速度-密度模式的速度梯度中包含了高波数成分。在本测试的观测系统中,两种梯度的深层照明范围存在较大差异:阻抗-速度模式中速度梯度主要利用了大偏移距数据,由于无法接收到模型两端位置产生的大偏移距数据,随着深度的增加其照明范围逐渐减小;而速度-密度模式由于能够接收到来自模型两端的近偏移距数据,在模型两端的深层位置其梯度照明范围更广。该模型中浅层的陡倾角断层遮挡了深层反射,深层的速度梯度差异减小。

初始速度较为准确时,采用常规的速度-密度模式进行全波形反演速度建模可以取得理想的效果,但当初始速度精度不够时,速度反演结果不理想(图6)。为此,我们首先采用阻抗-速度模式进行低波数速度反演(图9),并以此作为新的初始速度模型采用速度-密度模式进行高波数速度反演得到高分辨率速度模型(图10)。从图10可以看出,MarmousiⅡ模型的断层形态和位置得到了充分刻画,断层边界清晰,地层起伏与真实模型吻合。同时,由于该模型中浅层陡倾角断层发育,深层反射被遮挡,且深层缺失较多的大角度地震数据,因此深层速度反演的分辨率不足。鉴于阻抗-速度模式下已经反演得到了低波数的速度,在利用速度-密度模式进行高波数速度反演时,选取小偏移距地震数据作为观测数据进行全波形反演,不仅可以提高反演精度,而且可以提高计算效率。

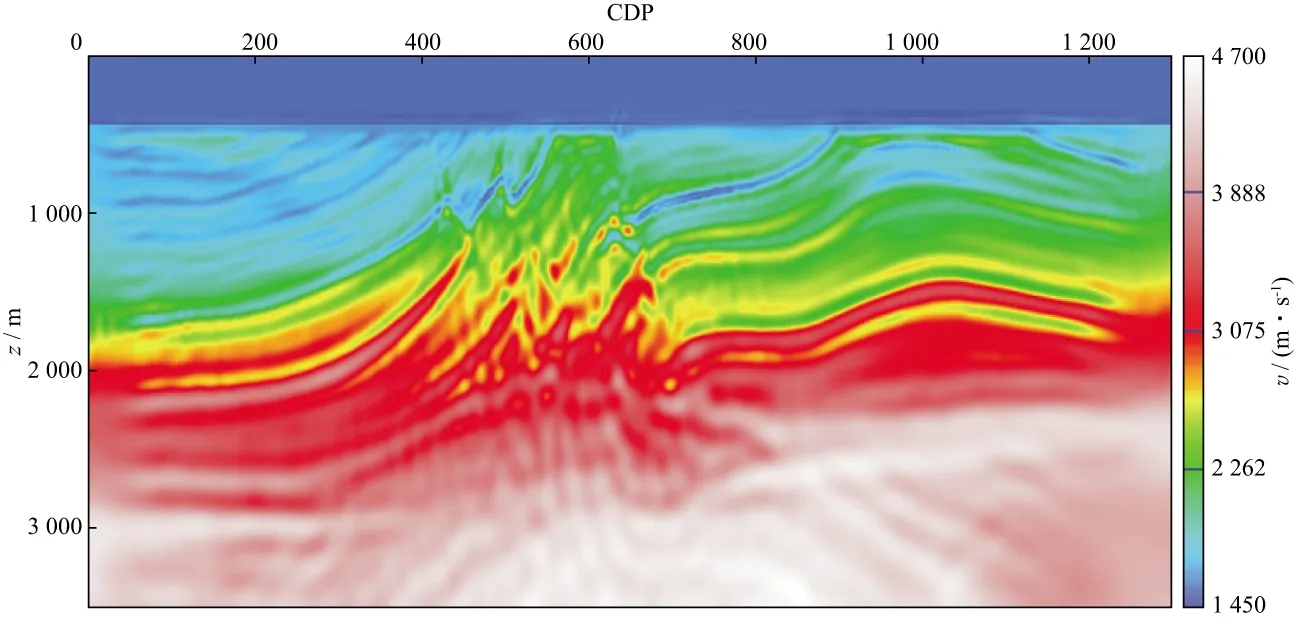
图6 直接进行速度-密度模式全波形反演的速度

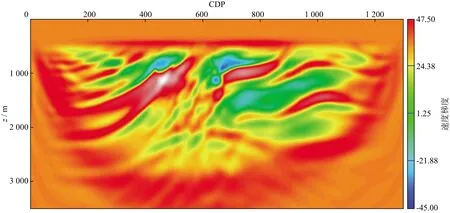
图7 直接进行阻抗-速度模式全波形反演的速度梯度

图8 两种模式下的速度梯度之差

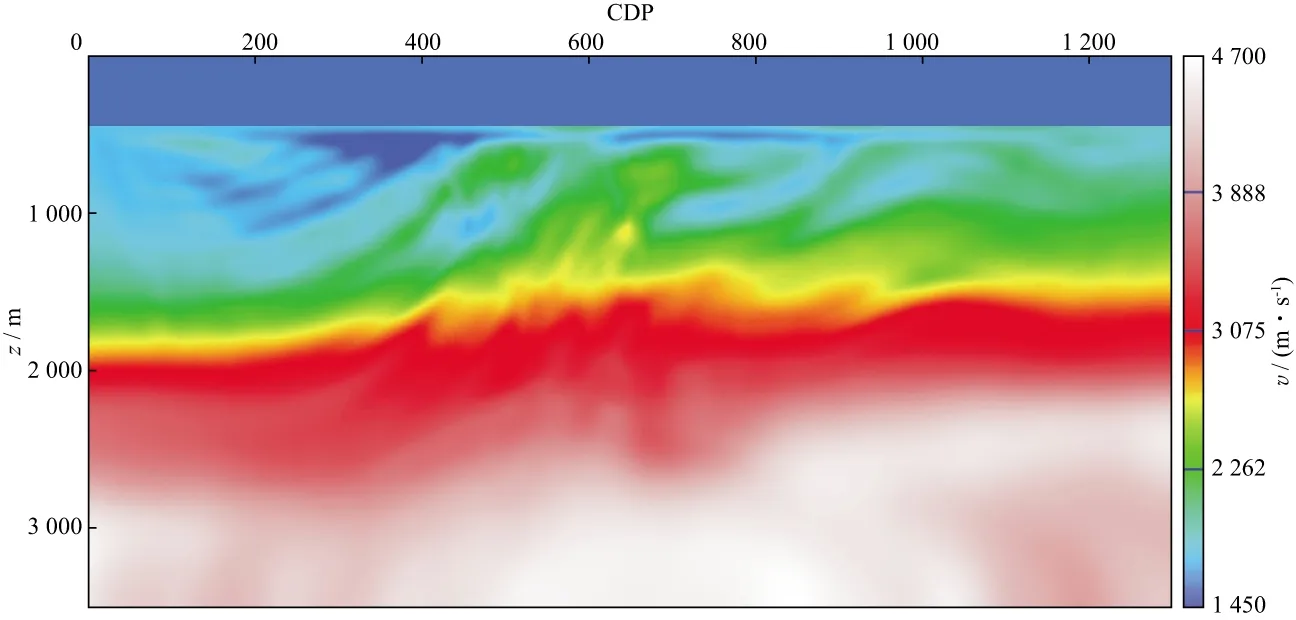
图9 利用阻抗-速度方程反演得到的低波数速度

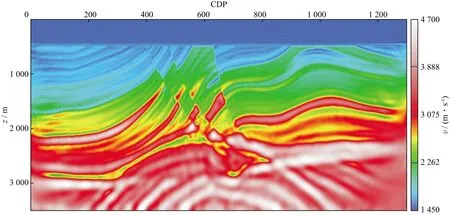
图10 以图9为初始速度利用速度-密度方程反演得到的高波数速度

4 结论与认识

本文研究了阻抗-速度和速度-密度参数化模式中的速度反演,给出了基于波动方程转换的时间域多尺度全波形反演速度建模策略,在时间域实现了从低波数到高波数的多尺度全波形反演,通过MarmousiⅡ模型测试,验证了方法的有效性。研究结果表明:

1) 利用阻抗-速度方程可以先拟合出观测数据中的大偏移距成分,实现低波数速度模型的全波形反演,通过方程转换,再利用速度-密度方程模拟小偏移距地震数据,可以实现从低波数到高波数的多尺度时间域全波形反演速度建模。

2) 在初始速度模型不够准确的条件下,本文方法能够正确刻画断层形态,断层位置准确,断层边界清晰,反演结果与真实模型吻合。

3) 本文反演方法基于波动方程转换,避免了混合域全波形反演的数据转换问题,同时,通过优化的数据匹配控制可以进一步提高计算效率,因而适用于实际大规模数据的全波形反演速度建模。