基于复数域波场分解的保幅逆时偏移成像方法
李 博,刘志成,李小爱,许 璐
(1.中国石油化工股份有限公司石油物探技术研究院,江苏南京211103;2.中国石油化工股份有限公司西北油田分公司,新疆乌鲁木齐830011)
基于双程波动方程的逆时偏移方法在实际工业生产中能够应对各种复杂的地震波成像问题[1-2],因此一直都是石油勘探行业的研究热点。该方法采用有限差分方法进行震源波场正传与检波点波场反传,并将两种波场沿时间方向做零延迟互相关成像[3-4]。利用双程波波场模拟算法能够正确描述反射波、折射波、回转波、多次波等复杂波场现象,处理复杂构造地区的地震成像问题。然而,由于波场传播算子没有明确区分波的传播方向,引入了偏移噪声[5],因此当入射波场与反射波场传播方向相同时,将产生物理上不存在的成像噪声,表现为低频强振幅掩盖了真实的反射界面[6]。针对RTM成像低频噪声问题的处理方法主要可以分为两类:①减少背向反射波,降低噪声能量。如,BAYSAL等[7]采用无反射方程来减少背向反射波,但该方法一般只对垂直入射波应用效果明显;LOEWENTHAL等[8]采用大于波长长度的窗函数对模型慢度做平滑,减少了背向反射波;FLETCHER等[9]通过在波动方程中引入背向反射波衰减项压制偏移噪声;还有学者通过上下行波分解限制逆时偏移成像条件,对入射波场和反射波场分别成像以有效减少低频噪声的产生[10-14],但是该方法需要进行高维平面波分解,计算量巨大,进行多次高维傅里叶变换难以满足实际生产对工期的要求。②压制大反射角成像能量。如,YOON等[15]采用Poynting矢量成像条件在成像前进行震源波场和检波点波场的传播角度估计,根据入射线与反射线的夹角进行加权叠加,达到压制偏移噪声的目的;ZHANG等[1]、XU等[16]提出叠后拉普拉斯滤波等价于对逆时偏移角度道集进行大角度切除,在偏移完毕后进行拉普拉斯滤波压制低频噪声;杜启振等[17]从计算效率和处理效果两个方面对压制低频噪声的各种策略进行了深入分析,指出拉普拉斯滤波是目前工业应用中最经济的方法,波场分解成像是效果最好的方法。
但是,上述两类方法都有一定的适用条件。如减少背向反射波方法必须进行波动方程改造,增加衰减项或辅助变量,计算效率很低,或者需要光滑的背景速度模型,难以符合复杂的地质情况;叠后拉普拉斯滤波方法实现简单、计算效率高,在实际应用中得到了广泛应用,但该方法保幅性较差,同时会损失成像剖面的低频信息。本文提出一种先利用复数波场重构地震数据,再通过复数波场运算实现方向波场分解的成像方法,并利用GPU平台在几乎不增加计算量的同时完成波场保幅成像。
1 复数波场构建及波场分解
通常认为采用声波方程直接模拟得到的全波场进行偏移成像具有成像倾角无限制的优势[1-4],但由于目前地震成像理论的基础仍然是CLAERBOUT提出的褶积成像条件或反褶积成像条件[18],不是地震反射波成像的充分必要条件,在逆时偏移中除了产生低频成像噪声外,还有可能产生虚假成像结果,因此必须考虑地震波的瞬时传播方向,选择真实的地下一次反射波进行成像。
首先,将炮点与检波点波场进行方向波分解。以上下行波为例,可以将全波场表达为:
(1)
式中:S(t,x)、R(t,x)分别表示震源、检波点全波场;SD(t,x)、RD(t,x)分别为震源、检波点的下行波场;SU(t,x)、RU(t,x)分别为震源、检波点的上行波场。若采用(1)式的波场表达方式,则逆时偏移成像条件可以写为:
(2)
式中:IDU(x)与IUD(x)为传播方向相反波场的成像结果,反映了地下界面成像信息;IDD(x)与IUU(x)为传播方向相同波场的成像结果,对最终成像结果不会产生贡献,只产生偏移噪声和假象。因此可以直接舍弃IDD(x)和IUU(x),公式(2)写为:
(3)
从公式(3)可见,实现方向波分解成像必须同时获得公式(1)中的所有行波分量。双程波模拟通常采用有限差分方法,只能获得全耦合的波场,但是可以通过频率-波数域分解,分别获得行波分量。以公式(1)中的震源波场为例,通过傅里叶变换可以得到震源波场的频率-波数域表达式:
(4)
其中,S(ω,k)、SD(ω,k)、SU(ω,k)分别是S(t,x)、SD(t,x)、SU(t,x)的频率-波数谱。根据方向波传播特性,可以获得上下行波分量的表达式:
(5)
其中,kz表示深度z方向的波数。可见,已知S(ω,k),就可以很容易获得上下行波分量。类似地,可以得到检波点反传波场的上下行波场表达式。由(5)式可知,波场的方向由频率-波数的符号决定,若直接进行波场分解成像,则需要进行沿时间和深度方向的正、反傅里叶变换,对于三维逆时偏移算法而言,其计算量非常大[19-20]。LIU等[11]、YOON等[15]采用Poynting矢量方法在每个成像时刻估计波场的瞬时传播方向,对于简单模型取得了较好的应用效果,但是该方法在复杂波场情况下无法正确识别同一位置的多个传播角度和波峰波谷的瞬时传播方向,实际应用中仍存在较多的噪声影响。本文提出通过希尔伯特变换得到波场的虚部,将原始波场作为实部,构建复数波场优化波场分解的高效计算方法。复数波场的表达形式如下:
(6)

(7)
分析公式(5)可见,如果能确定频率ω的符号,则只需要判断kz的符号即可获得分解后的波场频率-波数谱。将复数波场的频率-波数谱公式(7)代入公式(5),即可得到上下行波的复数波场表达形式:
(8)
由(8)式可知,只要构建了复数波场,在每次成像条件应用前进行一次深度方向的傅里叶变换和反变换,即可获得上下行波分解后的波场。将分解后的上下行波场分别代入公式(2)成像条件,即可获得成像结果。
2 复数波场逆时偏移实施方案
根据公式(6)进行复数波场的构建需要进行全波场在时间方向的希尔伯特变换,但是常规逆时偏移仅仅保存几个时间步的波场信息,无法进行时间方向的希尔伯特变换。LIU等[11]根据波动方程的有限差分算子具有线性时不变性,将地震数据先进行希尔伯特变换再实施波场延拓,获得了复数波场的虚部,但是该方法需要进行两次波动方程的延拓,计算量和存储量各增加一倍[13]。
依据公式(8)对复数波场上下行波的分解性质(kz≥0表示上行波,kz≤0表示下行波),从全波场S(ω,k)出发,先考虑kz的符号再区分频率的符号位,同样可以获得上下行波分解方程:
(9)
其中,
(10)
将公式(9)所示的上下行波分解方程同时应用于震源波场和检波点波场,并代入公式(3)所示的成像条件,可以得到如下复数波场成像条件:
(11)
其中,SHz(t,x)和RHz(t,x)分别表示震源波场S(t,x)和检波点波场R(t,x)在深度z方向的希尔伯特变换。公式(11)所示的复数波场成像条件可以推广到左右行波分解成像,只需将希尔伯特变换的方向替换为水平方向即可:
(12)
其中,SHx(t,x)和RHx(t,x)分别表示震源波场S(t,x)和检波点波场R(t,x)在水平方向的希尔伯特变换。
从公式(11)和公式(12)可以看出,在常规逆时偏移实施过程中,只要对成像前的震源和检波点波场进行空间的希尔伯特变换,就可以在不增加存储量仅仅增加很少计算量的条件下完成不同方向的行波分解成像,具体实施方案如图1所示。目前逆时偏移技术在实际应用中可借助GPU的强大计算能力来实现[21],希尔伯特变换可以通过空间域褶积[20]在GPU上实现并行计算,因此本文复数波场逆时偏移方法的计算量与常规逆时偏移方法基本相当。

图1 复数波场逆时偏移实施方案
3 模型数据测试
采用三维盐丘模型数据对方法进行了测试。该模型纵横方向13500m ×13500m,垂直深度方向5000m,数据采样点数为451×451×501,采样间隔为30m×30m×10m,等间隔激发3333炮,检波器在深度z=0全网格共16×104道接收,子波为主频20Hz的雷克子波,速度模型和单炮记录见图2。从单炮记录看,直达波、反射波、绕射波丰富,宽方位采集方式对于盐下隐蔽构造的照明更好。
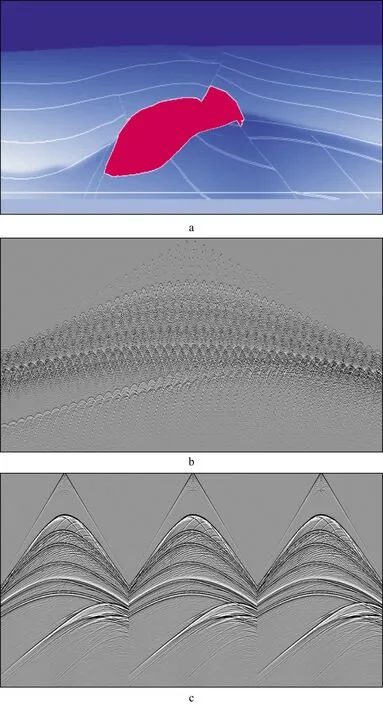
图2 三维盐丘模型和单炮记录a 三维盐丘速度模型; b 采集的单炮数据; c 单炮数据放大显示的3个检波器排列
实际计算使用10块NVIDIA-GPU K10卡,进行了常规逆时偏移成像、Laplace滤波、复数波场逆时偏移成像,结果如图3、图4所示,计算效率如表1所示。由图3可见,在复杂盐丘模型中利用本文方法进行波场分解可以分别获得上下、左右行波的波场。从分解效果来看,分解后的波场(图3c至图3f)相比双程波波场(图3b)几乎没有残余干扰信息,能够满足地震成像的需求。由图4可见,常规逆时偏移成像结果被强低频噪声覆盖(图4a),难以准确识别地层位置;通过Laplace滤波对常规逆时偏移剖面进行低频噪声压制后(图4c),可以清晰地看到地震反射层位置。工业界逆时偏移软件通常采用RTM+Laplace滤波这种组合方式进行成像[22],由于Laplace滤波是空间二阶导数,与RTM直接输出的振幅存在数量级的差异,因此不能进行噪声提取得到噪声剖面,只能获得成像剖面。本文复数波场逆时偏移方法根据公式(10)、公式(11)所示的联合成像条件实现波场分解成像,不仅可以输出成像剖面(图4d),而且能够输出噪声剖面(图4b)。

图3 盐丘模型的波场快照a 盐丘局部模型; b 双程波波场; c 上行波波场; d 下行波波场; e 左行波波场; f 右行波波场

图4 成像剖面及噪声 a 常规全波场RTM剖面; b 复数波场逆时偏移所压制的噪声; c Laplace滤波后的RTM剖面; d 复数波场RTM成像剖面
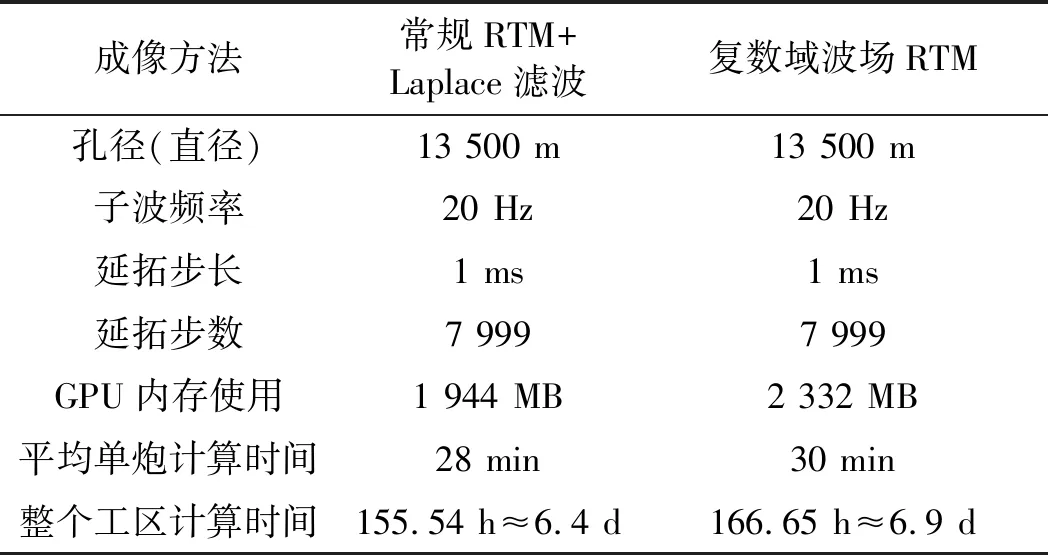
表1 三维盐丘模型计算参数与效率统计
从低频噪声的压制角度来分析,RTM+Laplace滤波的方式在压制低频噪声的同时损失了一些低频有效信息,尤其是高陡反射界面(盐丘右侧)处损失严重。本文复数波场逆时偏移方法则能够在有效压制低频噪声的同时,保留低频有效信号,使盐丘边界的高陡构造成像更准确,水平同相轴的成像更聚焦,波阻特征更明显,信噪比更高。图4b所示的噪声剖面上没有反射界面的能量损失,表明本文复数波场逆时偏移成像方法保幅性更高,并且解决了逆时偏移的低频噪声压制所带来的信号损失问题。
从表1可见,偏移孔径设定为13500m、深度5000m,完全覆盖了整个计算模型。在保证稳定性条件的前提下取1ms延拓步长进行波场模拟,时间长度为8s,延拓步数为7999步。计算过程中,单个模型参数的三维体大小为388MB,常规的RTM方法需要5个模型大小的GPU存储量,复数波场RTM方法需要增加一个模型空间用于存储波场希尔伯特变换的结果,因此是6个模型大小的存储量,与常规RTM相比增加了20%的GPU存储需求。在计算效率方面,复数波场RTM单炮计算时间增加了约7.5%,整个工区3333炮数据在10块GPU上完成,常规RTM需要6.4d,复数波场RTM需要6.9d,增加的时间很少,基本可以忽略不计。
4 实际数据应用
为了验证本文方法在实际资料处理中的适用性,选择我国东部地区某实际地震资料进行了测试(图5、图6)。工区内地下构造复杂,断裂发育,尤其是深大断层边界刻画是该工区需要重点落实的目标。针对高陡断面波的成像,逆时偏移方法理论上具有90°倾角的成像能力,但是采用常规RTM+Laplace滤波方法进行成像时,由于Laplace滤波在压制低频噪声的同时会损失低频高陡构造断面波能量,低频高陡构造成像效果不佳(图5a,图6a)。图5b、图6b为本文复数波场逆时偏移方法直接输出的成像结果,相比常规方法的成像结果在断面波成像方面有明显的优势。实际资料测试结果表明,本文方法在低频信号的保护方面具有一定的优势,成像保幅性更好。

图5 实际资料逆时偏移结果对比(主测线)a RTM+Laplace滤波后的成像剖面; b 复数波场逆时偏移成像剖面

图6 实际资料逆时偏移结果对比(联络测线)a 常规RTM+Laplace滤波后的成像剖面; b 复数波场逆时偏移成像剖面
5 结束语
本文研究了复数波场逆时偏移方法,解决了逆时偏移过程中同时进行波场分解成像的计算及存储问题,在计算量微幅增加并保证计算精度的条件下,实现了上下、左右行波分别成像,给出了复数波场逆时偏移在GPU平台上的实现流程。模型数据测试结果表明,本文方法能在计算量和存储量少量增加的条件下,实现地震波场的分解成像,在低频保护方面优于传统的RTM方法,成像保幅性更好。实际资料测试结果表明,本文方法针对复杂高陡断裂系统的成像效果优于传统RTM方法,尤其在低频断面波成像方面具有较明显的优势。实际地震资料成像中可以兼顾成像效果与计算效率,采用本文方法进行低频保护的行波分解成像,提高深层断裂系统的识别能力,落实构造圈闭。

