高层双子楼布局方式对建筑风环境的影响
■ 赵 群 ZHAO Qun 赵晋鹏 ZHAO Jinpeng 李峥嵘 LI Zhengrong
0 引言
随着城市的迅速发展和建筑技术的提升,源自对称之美的双子楼、双子塔成为众多城市的靓丽风景线,如纽约双子塔、吉隆坡双子塔、厦门双子塔等。双子办公楼在城市建筑群中屡见不鲜,两栋建筑之间连接形成的大空间区域提升了空间利用率,体现了设计之美。为保证办公人员获得更好的观察视角,双子办公楼之间往往存在一定的错位距离,因而在两栋平行建筑之间区域(街通道)形成了独特的风环境,建筑之间的风速大小和通风效果成为关注的重点。
自20世纪80年代起,已经有许多学者对平行建筑之间区域的流场特征进行了详细研究。Oke[1]等人提出当来流方向垂直于建筑街通道方向时,背风街通道内的流形可以分为爬越流(skimming flow)、尾流扰流(wake interference flow)和孤立粗糙流(isolated roughness flow)等3类; 随后,Chan[2]等人在此基础上分析了街通道几何参数(高宽比、长高比及建筑相对高度比)对流场特征和污染物扩散作用的影响;刘朔[3]研究了两栋并列布置的建筑在不同建筑间距和建筑高度下周围速度场和压力场的变化情况,指出相邻建筑存在强烈相互影响的临界间距为两倍的建筑高度。Bolcken[4]则通过风洞试验研究了迎风街通道在不同的建筑间距下的速度分布情况,指出当建筑间距过小或过大时迎风街通道内的文丘里效应均不再显著。显然,目前的主要研究集中于来流风与街通道平行或垂直两种极端情况,而对其余风向角情况和双子楼之间存在错位的研究相对较少。
本文采用数值模拟方法研究在不同来流风向下两栋平行建筑之间的风环境,分析不同布局下的双子楼之间区域内行人高度处的舒适性和通风效果。
1 数值模拟
1.1 建筑模型的选取
本文选取长(L)、宽(W)均为20m、高(H)为60m的建筑为研究对象,两栋建筑间距(M)确定为20m。如图1所示,为阐述简洁,先给出风向角α和错位距离S的定义。风向角反映了来流风的方向,定义正北向来流风的风向角为0°,沿顺时针方向逐渐增大。错位距离反映两栋建筑在南北轴向上的相对位置,东侧建筑偏北时的S为负值,反之为正值。本研究中,选取α=0°,15°,30°,45°,60°,75°,90°;S=0,(±1/4W),(±1/2W),(±3/4W),(±W)。
1.2 边界条件的确定
依据AIJ[5]规定,选取最高建筑的高度作为特征长度H,建筑群上游、两侧及上部的计算域长度均为5H,下游计算域长度为15H(图2),图中阴影区域代表两栋研究建筑。采用结构化网格和非结构化网格相结合的方式划分网格。计算域入口采用速度入口,出口选择压力出口,两侧边界及顶部边界均采用对称性边界条件。来流边界条件选用指数型:
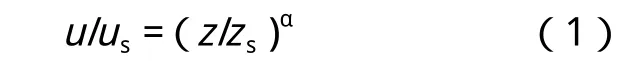
式中,us—参考高度zs=10m处对应的风速;
u—任意高度z处的风速;
α—大气边界层厚度指数。
湍流动能kz的垂直分布可由湍流强度Iz的垂直分布估算得到。大气边界层中:
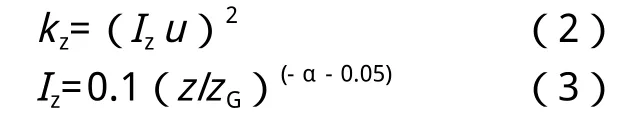
式中,zG—由周围地形确定的大气边界层厚度。
湍流耗散率εz的垂直分布由公式(4)确定:
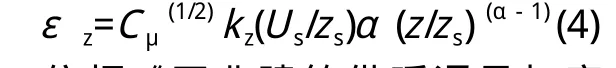
依据《工业建筑供暖通风与空气调节设计规范》(GB 50019—2015)规定,选取上海市冬季平均风速作为参考高度10m处的来流风速,速度值为3m/s。依据《建筑结构荷载规范》(GB 50009—2012)选取高层高密建筑群的大气边界层厚度指数为0.3,由地形确定的大气边界层厚度为550m。湍流计算模型采用标准k-ε模型,壁面函数选用标准壁面函数;差分格式为二阶迎风差分。当监测点的k、ε残差达到10-6,速度残差达到10-3,且监测点的速度值趋于稳定时,认为计算结果收敛。
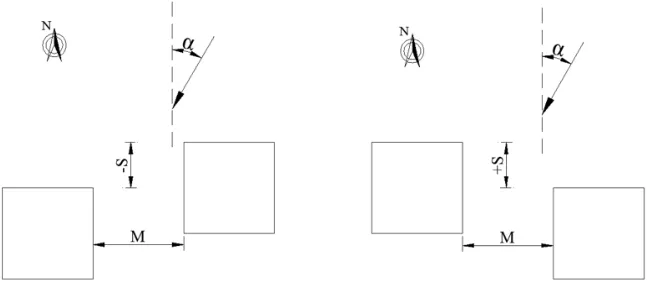
图1 不同错位距离及风向角的定义
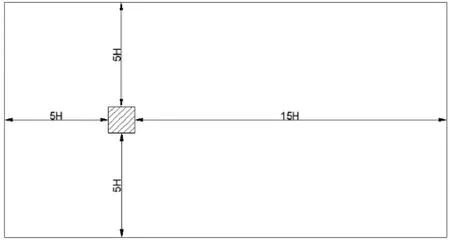
图2 计算域的俯视图
1.3 网格独立性验证
本文以风向角15°、建筑错位距离0m作为基本条件,以中等网格的速度模拟结果为参照,分别计算粗糙网格和精细化网格带来的模拟结果与中等网格模拟结果之间的平均相对误差(S1、S2),并根据结果确定本文采用的网格数量。其中,中等网格数目约为110万个,粗糙网格尺寸为其数量的一半,而精细化网格为中等网格数量的两倍。选取1.5m、10m、30m和50m高度平面内均匀分布的监测点(图3)作为计算点,S1、S2计算公式如下:

式中,vi,coarse、vi,medium、vi,fine分别为在粗糙网格、中等网格、精细化网格条件下,第i个监测点的速度值。结果显示:S1=3.5%,S2=2%。说明网格数目和网格质量对于计算结果准确性的影响不显著。出于计算机计算能力和计算时长的考虑,本文模拟均采用中等网格。
2 风环境评价指标的确定
本研究旨在满足行人舒适感的前提下,提高建筑间气态污染物衰减速度,为双子楼的建筑布局设计提供参考。因此,本部分选取以下4个评价指标。
2.1 放大因子
放大因子体现了建筑相对位置对风速大小的影响情况,用于衡量行人舒适感:

图3 不同高度平面及测点的选取

式中,Ai—不同位置的放大因子;
Ui—不同位置行人高度的风速;
Uref—未受到建筑影响的参考位置处自然来流风速。
同时,定义Aavg为特定区域内平均放大因子,Amax为特定区域内的最大放大因子。ShiX等[6]总结了众多学者对放大因子的研究成果,提出行人舒适的平均放大因子临界值为1,最大放大因子临界值为1.5。
2.2 无量纲空气流量
无量纲空气流量反映了建筑群中的空气流动情况,该值越大,反映群中气态污染物衰减速率越高。在特定来流风向条件下,流入或流出建筑之间特定界面的无量纲空气流量可由以下公式计算:
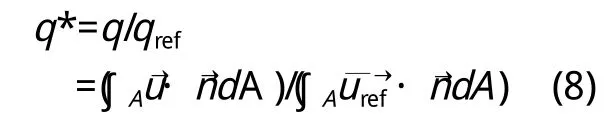
式中,u—建筑间气流截面上不同位置的速度矢量;
n—截面的法线方向;
A—该截面所对应的面积;
2.3 冠层平均速度和界面交换速度
当来流风与双子楼街通道呈现较大夹角时,因建筑间相互遮挡作用显著,流入或流出的空气流量较小,难以准确反映内部的通风效果差异性,宜采用冠层平均速度UC和界面交换速度UE来表征背风街通道的通风情况。
冠层平均速度UC是基于建筑群内建筑表面前后压差等效得到的平均速度,具体计算公式如下:

式中,ρ—空气密度;
FP—建筑前后表面的压力差;
CD—建筑阻力常数,依据多数学者的研究结果,立方体建筑的阻力常数一般为1;
AF—建筑迎风面积。
界面交换速度UE反映了建筑街通道顶部与外界的动量交换情况,具体计算公式为:
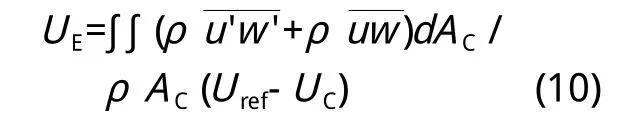
AC—建筑群顶部任意区域的面积;
Uref—参考高度为2.5H(H为建筑群的平均建筑高度)处的速度。
3 结果分析
本部分重点讨论错位距离S和风向角α对各评价指标的影响。
3.1 放大因子
图4反映了错位距离S和风向角α对平均放大因子(Aavg)的影响情况。
(1)当α在0°~45°范围内变化时,Aavg随S的变化规律基本一致:随着S的增加,Aavg先增后减,在S=0时达到最大。其原因在于风向角较小时,建筑之间的相互阻挡作用并不显著,相同的来流条件下流入街通道的空气流量差异不大,而S的增加导致建筑作用区域增大,因而街通道内的平均速度(即Aavg)减小。
(2)随着α的进一步增大,特别是当α达到75°及以上时,Aavg则变为先减后增;当α达到90°时,以S=0的状态为对称,形成鲜明的陡增陡降趋势。其原因在于迎风街通道转变为背风街通道的过程中,建筑之间的相互遮挡作用增强,而为正的错位距离增加又削弱了建筑之间的遮挡作用,使Aavg随即增加迅速。
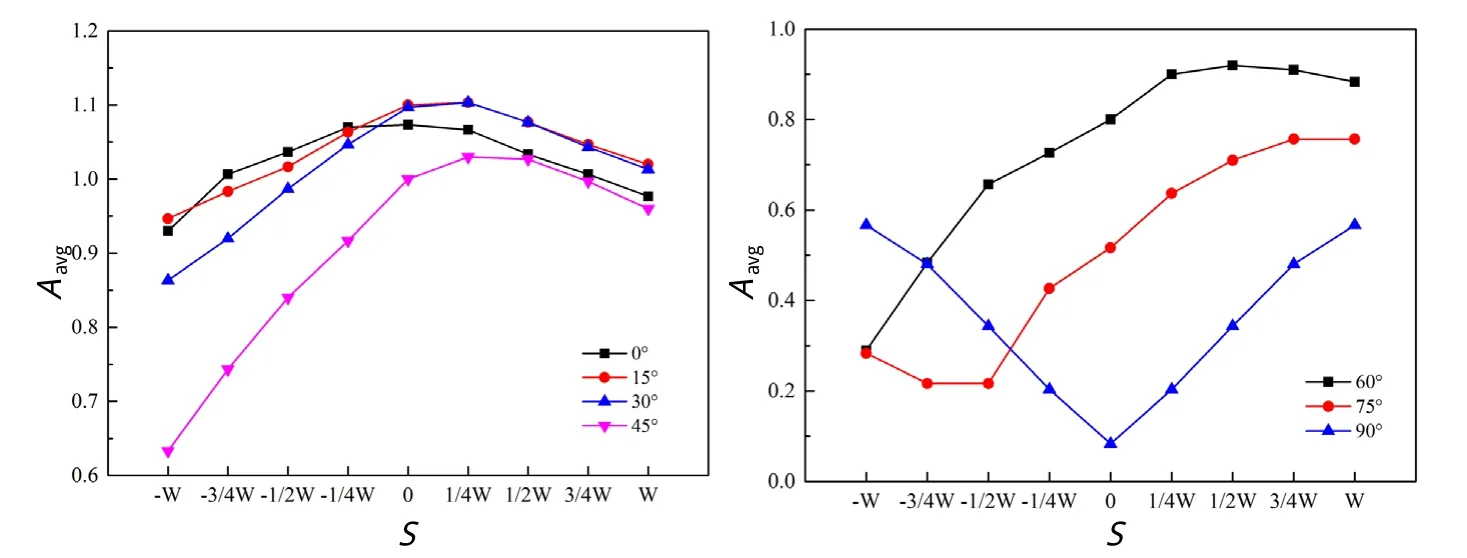
图4 错位距离和风向角对平均放大因子的影响
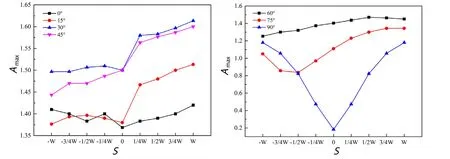
图5 错位距离和风向角对最大放大因子的影响
图5 给出了最大放大因子(Amax)随错位距离和风向角的变化情况。当α在0°~45°范围内变化时,Amax的总体趋势是随S的增加而增加,且从S=0开始,Amax增加迅速。这是因为S为正时,角流作用和文丘里效应的叠加使Amax显著增大。当α在60°~90°之间变化时,其基本规律与图4一致,这里不再赘述。
根据图4和图5显示,当α=0°~15°时,仅仅在错位距离S=W情况下,Aavg<1且Amax<1.5,满足人员的风舒适要求。但此种情况下,建筑之间的错位距离过大,在高层高密建筑中对土地的利用相对较小。当α=30°或45°,且错位距离S为0或负值时,Aavg<1,Amax则接近1.5,满足人员的舒适性要求。当α>45°时,任意错位距离条件下的Aavg<1且Amax<1.5,同样满足人员的舒适性要求。
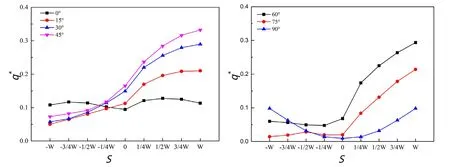
图6 错位距离和风向角对顶部空气流量的影响
3.2 无量纲空气流量
图6 为不同风向角和错位距离下的顶部无量纲空气流量(q*)的变化情况。
当α在0°~90°变化时,除了0°和90°这两种对称情况外,无量纲空气流量q*随着S的增加总体呈现增大趋势,且当S为正时,增加速率明显。当α=45°时,q*在不同S条件下达到最大,这是因为当α较小时,建筑之间的相互遮挡区域较小,随着α的增加,建筑棱角的影响导致顶部脉动情况增强,建筑顶部的空气流量显著增加;而当α>45°时,建筑之间的遮挡面积增大,建筑爬越流或尾流扰流作用显著,通过建筑顶部的空气流量减少。如表1所示,在错位距离S=0的条件下,相比于风向角α=0°,α分别为15°、30°、45°时,对应的顶部无量纲空气流量q*分别增加18.8%、57.7%、74.7%;而α=60°、75°、90°时,对应的q*分别减小28.3%、79.1%、90.3%。
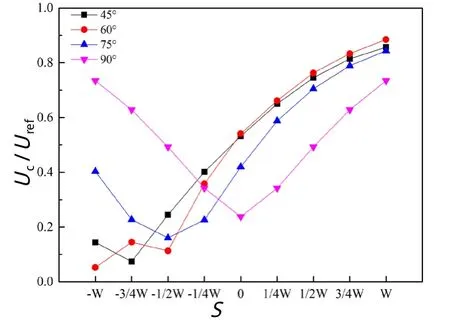
图7 错位距离和风向角对冠层平均速度UC的影响
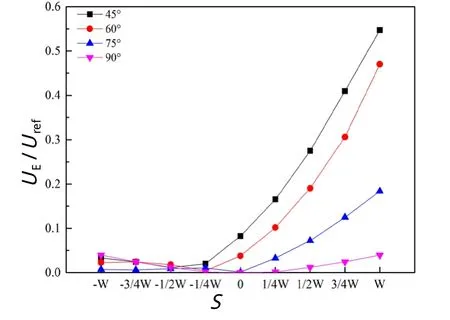
图8 错位距离和风向角对界面交换速度UE的影响
3.3 冠层平均速度和界面交换速度
图7 和图8反映了错位距离和风向角对冠层平均速度UC和界面交换速度UE的影响。显然,随着S的增加,UC和UE呈现不同程度的先抑后扬趋势,且拐点处的S值略有不同。尤其是S>0时,S的存在削弱了建筑之间的遮挡作用,冠层平均速度UC和界面交换速度UE均随着S的增加而迅速增大。负错位距离S的存在强化了建筑之间的遮挡作用,UC和UE均处于较低水平。但是,当α>75°时,负向错位距离过大反而弱化了建筑之间的相互遮挡作用,下游建筑能够直接面对来流风的作用,UC/Uref随着错位距离的增大而增大;当α=90°这一极端情况时,正错位距离和负错位距离的存在均有效促进了建筑之间的通风效应。

表1 不同风向角下q*的变化情况
基于以上分析,我们可以得出下面结论:①对于α=0°~15°的情况,只有当双子楼的错位距离足够大,使之完全成为两栋独立的建筑时,两栋建筑之间区域内的风环境满足行人舒适性要求,但此时顶部空气流量相对较小,且此种布局方式对于土地的利用率极低;②对于α=30°或45°的情况,当错位距离为0或负值时,双子楼之间的风环境满足行人舒适性要求,但负向错位距离较大时,顶部空气流量相对较小,因此,此种情况下的错位距离应该位于(-1/4W)~0之间;③对于α>45°的情况,任意错位距离下的双子楼之间的风环境均满足舒适性要求,但错位距离为正值时,顶部空气流量、冠层内平均速度和界面交换速度均明显增大,同时,考虑对土地的利用率,推荐错位距离在1/4W~1/2W之间。
4 结语
综上所述,本文采用数值模拟方法,研究不同风向角和错位距离条件下两栋平行建筑之间的风环境,并采用放大因子、无量纲空气流量、冠层平均速度和界面交换速度对不同布局形成的风环境进行评价。当风向角α<45°时,随着正错位距离的增加,平均放大因子减小,而最大放大因子增大,流出建筑之间顶部的空气流量增大;当风向角α>45°时,随着正错位距离的增加,平均放大因子、最大放大因子、冠层平均速度和界面交换速度均明显增大,流出建筑之间顶部的空气流量同样增大。当错位距离S=0时,随着风向角α的增加,平均放大因子、最大放大因子、流出建筑之间顶部的无量纲空气流量先增大后减小,且基本均在α=45°时达到最大值。
由于双子楼一般均采用坐南朝北的并排布局方式,其布局主要结合不同城市的主导风向进行设计。我国各个城市夏季的主导风向基本为东南风,通过对称性分析可得当城市主导风向为南风时,为实现良好的风环境,可将双子楼进行偏转使建筑之间的通道与主导风向的夹角在30°左右;当城市主导风向为东南风时,双子楼之间的错位距离应该在0~1/4W之间选取;而当城市主导风向为南偏东60°~90°时,双子楼之间的错位距离应该在(-1/2W)~(-1/4W)之间选择。

