某会展中心风洞试验研究
刘 彪,黄用军
某会展中心风洞试验研究
*刘 彪1,黄用军2
(1. 华南理工大学土木与交通学院,广东,广州 510641;2. 深圳市欧博工程设计顾问有限公司,广东,深圳 518053)
通过对某会展中心北侧两个大跨波浪形悬挑屋盖的风洞试验研究,讨论了典型风向下屋盖的平均风压分布,同时对全风向角下屋盖平均风压、脉动风压与极值风压的分布进行了研究,并进一步探讨底部开敞对悬挑屋盖风荷载的影响。试验研究表明:屋盖整体以负压为主,除在迎风向的屋盖悬挑区域外,其他区域风压较小;屋盖局部特殊的体型可能产生“兜风效应”,从而显著增大风压;而底部开敞造成的“窄管效应”会显著增大开敞区域的风荷载,同时由于底部开敞减弱了气流的堵塞作用,使屋盖上表面风吸力有所减弱,对下表面风压力影响不大;总体而言,屋盖悬挑端在迎风向的体型系数基本在-1.5至-1.8范围。
大跨悬挑屋盖;风洞试验;风压系数;体型系数
随着我国经济建设的发展,大跨度空间结构被广泛地应用于体育场馆、会展中心和机场航站楼等大型公共建筑。由于大跨屋盖结构的使用要求,它往往具备质量轻、柔度大、阻尼小等特点,风荷载成为大跨屋盖结构的主要控制荷载[1]。
大跨度屋盖结构一般比较低矮,处于风速变化大和湍流度高的大气边界层中区域,而且由于外型复杂,其表面绕流和空气动力作用十分复杂。此类结构的抗风问题一直是风工程界研究的热点。国内外许多学者对典型的大跨度屋盖进行了大量的风洞试验研究[2-4],而对于带有悬挑端的大跨屋盖结构,其悬挑端的风场绕流尤其复杂。我国现行的《建筑结构荷载规范(GB50009-2012)》[5]缺乏这类结构相应的风荷载设计数据。为了确保结构的设计安全,需要通过风洞试验进行研究。
鉴于此,本文以某会展中心的大跨悬挑屋盖为研究对象,通过风洞试验讨论了屋盖的风压分布特性,并进一步探讨底部开敞对悬挑屋盖风荷载的影响,最后给出此类屋盖悬挑端的体型系数,为类似大跨屋盖结构的抗风设计提供参考。
1 工程及试验概况
某大型会展中心在其最北侧对称布置了两个展厅,以下分别称为屋盖G和屋盖V。屋盖G南北宽250 m,中间有一条宽42 m的开敞通道,东西长210 m,屋盖四周均有不同程度的悬挑;屋盖V与屋盖G的体型和平面投影相同,但是比屋盖G整体高出2.9 m且底部全封闭。本项目风洞试验模型的几何缩尺比为1/250,如图1所示。采用中国规范中的A类地貌,图2为风速和湍流强度模拟情况。

图1 风洞试验模型
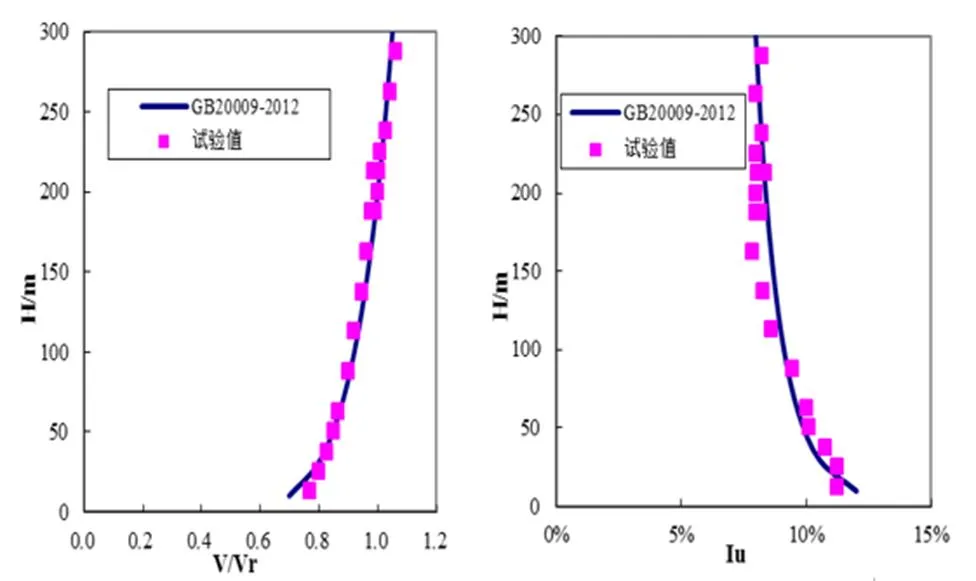
图2 A类风场的平均风速和湍流度剖面
风洞试验参考高度为0.6 m,该高度处的试验风速Vr为10.7 m/s。风向角间隔为10度,共36个风向角。为了更好地研究屋面的风荷载情况,在屋盖V和G的屋面上均匀对称布置了215个测点,屋盖V在悬挑区域布置69个双面测点,屋盖G因中部开敞总有95个双面测点。其中,屋盖的悬挑区域进行了测点加密处理。屋面测点布置图及风向角定义如图3所示。
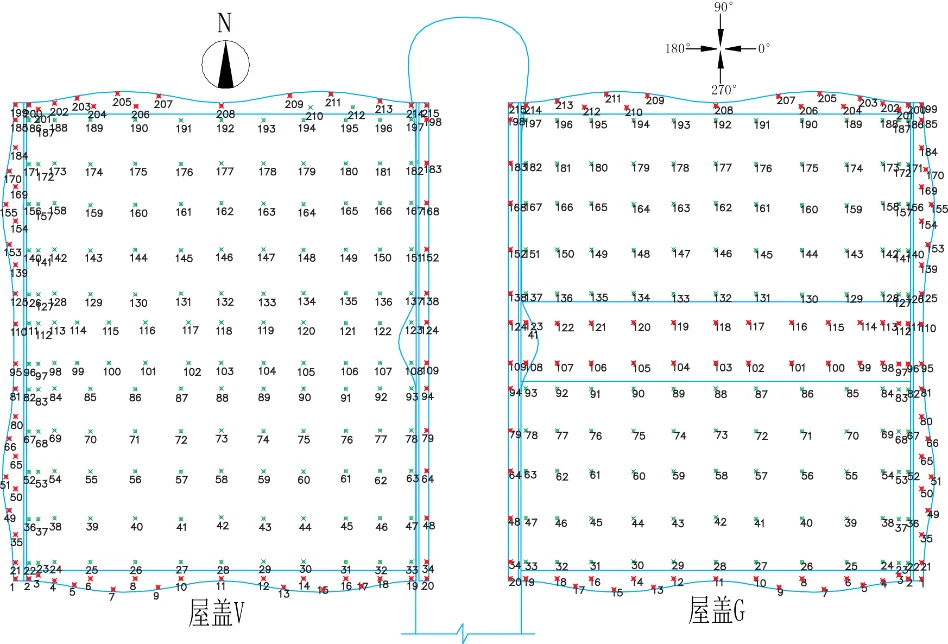
图3 屋盖测点布置及风向角定义
2 数据处理方法
试验中风压符号定义为:沿结构表面法线方向远离结构时为负压,表现为风吸;反之为正压。屋盖表面各点的风压系数由下列公式给出:
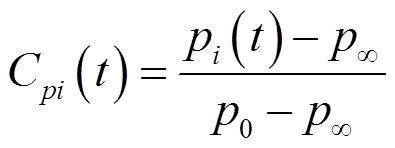
用于围护结构设计的极值风压系数的定义如式(2)所示:
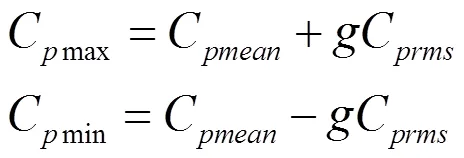
可按以下关系将风洞试验测得的风压系数变换为测压点的局部体型系数:
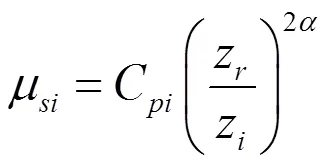
式中:z和z分别为试验选定的参考高度和测压点高度,为地貌粗糙度指数,μ即为第个测点的点体型系数。
3 试验结果分析
3.1 平均风压分布
考虑到V、G两个屋盖的不完全对称性,选取以下典型的风向进行分析:顺风向(V180°与G0°)、斜风向(V140°与G40°)、横风向(V90°与G90°)。图4(a)~4(c)给出了屋面V和G在顺风向、斜风向、横风向的平均风压系数等值线图。
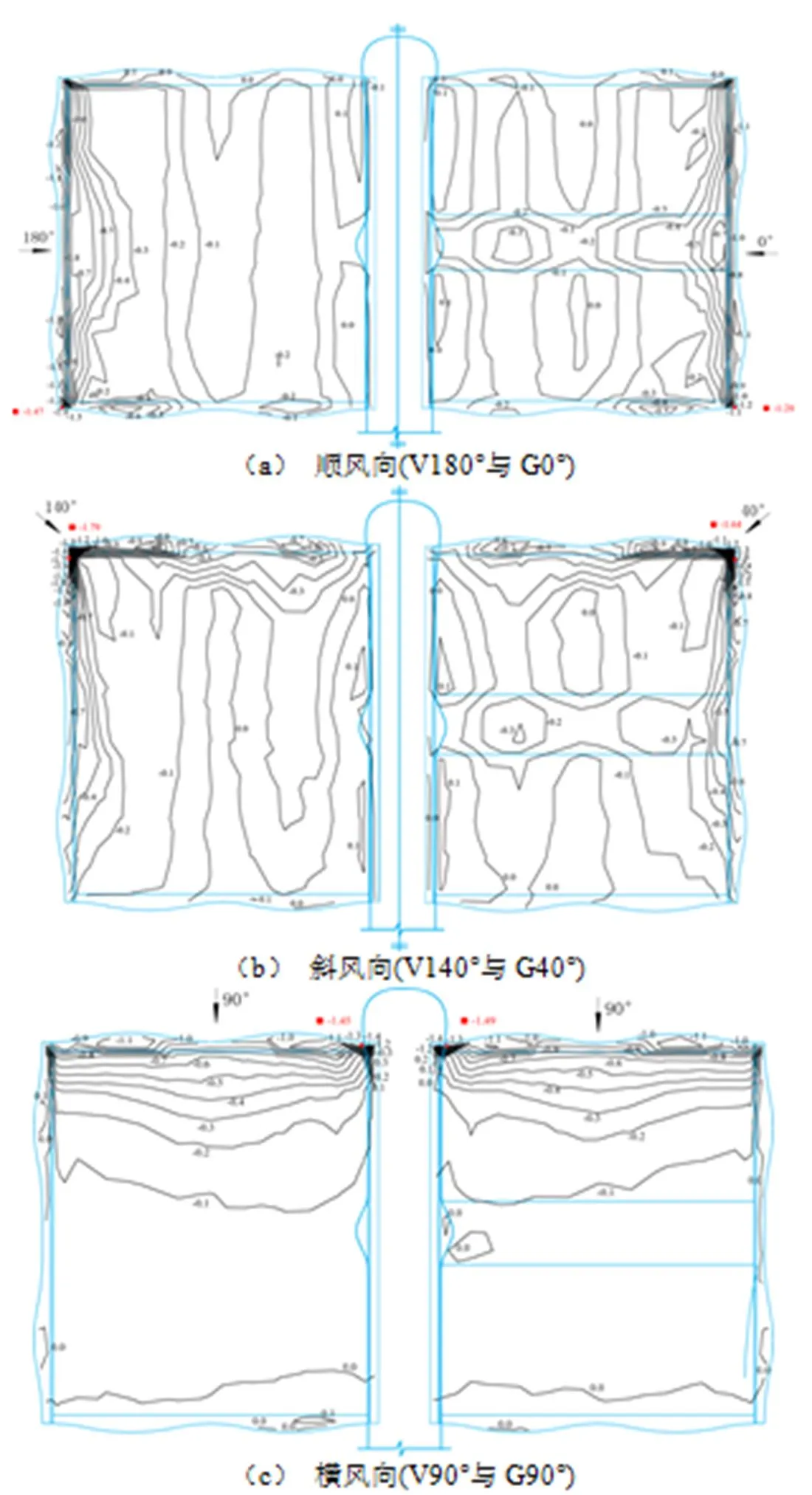
图4 典型风向角下平均风压系数分布图
在顺风向下,由图4(a)可知,屋盖悬挑前端产生较大负压,风压变化激烈。随着距离的增加,负压逐渐变小,到达波谷处风压接近0;经过第二个波时由于气流分离出现负压,在波峰处达到最大约为-0.1。屋盖G由于中间开敞,风流经中部的连通过道产生“上吸下顶”的叠加作用,故屋盖G的屋面中部开敞区域负压均大于屋盖V且未出现正压。屋盖V和G的平均风压系数最值分别为-1.47和-1.28,均出现在屋盖南侧的角区边缘。
当风为斜风向时,由图4(b)可知,屋盖的角部产生了明显的锥形涡[7],漩涡区域风吸力很大且变化剧烈。由于风向角为斜偏下方向,屋盖V和G平均风压系数最值均出现在角部偏下位置,分别为-1.79和-1.64。在下风向区域由于漩涡作用强度减小,风吸力迅速减小。
在横风向下,由图4(c)可知,屋盖G中部开敞区域几乎不受风,屋盖V和G的风压分布对称性很好。气流在屋盖前缘形成柱状涡,从屋盖前缘到中部,平均风压系数大致由-1.0逐渐减小到-0.1,在屋盖的下半部分风压很小,基本为0。最小平均风压系数出现在中央廊道与屋盖交界的角部区域,分别为-1.45和-1.49,远大于外侧角部边缘的风压系数-1.0。
3.2 全风向角风荷载分析
为了研究在不同风向角下的风荷载特性,选取屋盖V和G的角区测点200、北端挑檐波谷处测点208、外挑檐中部测点110以及屋盖中区的波峰测点160为分析对象,图5(a)~5(d)给出了四个测点平均风压系数和脉动风压系数随风向角的变化曲线。考虑到两个屋盖的对称性和差异性,为了便于比较,以风洞试验风向角为基准,屋盖G起始角为0°,角度按逆时针增加,屋盖V起始角为180°,角度则按顺时针增加。如50°则对应G50°和V130°。
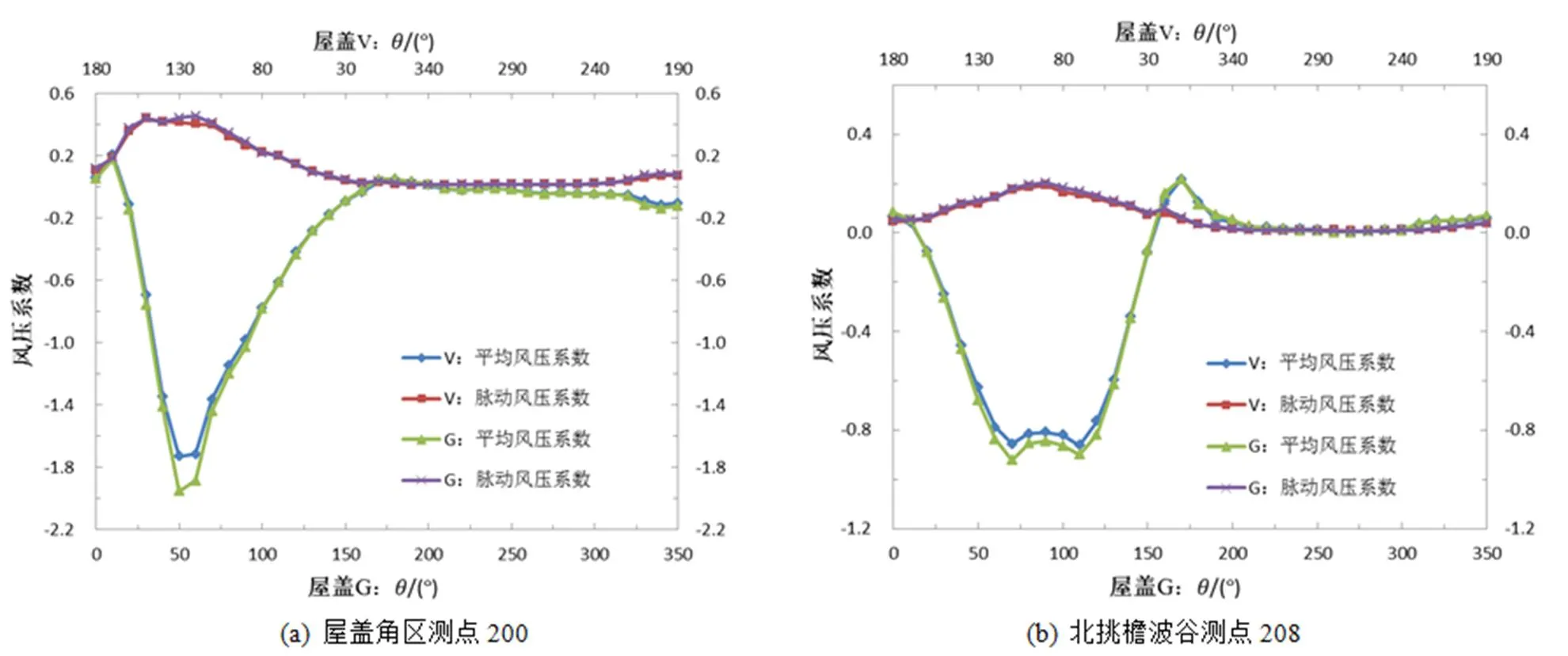
由图5(a)可知,测点200处于屋盖角区,当来流从顺风向变为斜风向时(0°~50°),平均风压与脉动风压均急剧变大。在50°时,受锥形涡作用,屋盖G和V平均风压同时达到极值且数值差异明显,分别为-2.0和-1.75;两者脉动风压系数在30°~70°范围均较大,约为0.45。当风向角为60°~160°,平均风压与脉动风压则迅速减小。随着风向角继续增加,由于屋盖处于下游,风压基本稳定在0左右。
由图5(b)可知,处于屋盖北挑檐波谷的测点208,变化规律与角区测点200相似,但风压变化没有角区测点剧烈,故其曲线轮廓则显得“矮胖”。由于该测点在屋盖中间,在0°~180°风向角下,平均风压系数与脉动风压系数变化曲线基本关于90°对称,但在某些风向角下平均风压为正压,在70°~110°区间,平均风压系数和脉动风压系数达到极值分别约为-0.9和0.2,但屋盖G的平均风压系数略大于屋盖V。
由图5(c)可知,外挑檐中部的测点110,风压系数变化曲线基本关于180°对称且脉动风压系数曲线基本重合。在0°~90°,平均风压系数从-1.05左右逐渐减小到0,在部分风向角屋盖G的风吸力强于屋盖V;在100°~180°时,出现较小的正压,且屋盖G的平均风压比V小一些。由于此测点处于屋盖G的开敞区域外沿,在部分风向角下该点的风场有所不同,在下风向,差异性明显减弱。
由图5(d)可知,对于在屋盖中区波峰的测点160,风向角在0°~350°时,平均风压系数与脉动风压系数均较小。波峰处由于气流分离作用而在全风向都表现为风吸,平均风压系数介于-0.1到-0.35之间,且屋盖G的负压略强于V。由于在中区波峰处气压已变得较缓和,风压脉动微弱,全风向脉动风压系数维持在0.05左右。
总体来说,屋盖V与屋盖G因体型对称其风压系数变化曲线基本一致。受锥形涡控制的屋盖角区测点200,风压系数随风向角变化明显且具有较大的极值。外挑檐波谷测点208和北挑檐中部测点110风压变化没有角区剧烈,其平均风压系数和脉动风压系数的极值大概只为屋盖角区的一半。在屋盖波峰位置的测点160,由于在此处尾流分离,故在全风向下其平均风压和脉动风压均很小。
对于大跨度悬挑屋盖而言,上吸风极值通常为最不利荷载。根据公式(2)本文给出用于指导围护结构设计的屋盖全风向角最不利极值负压分布如图6所示。
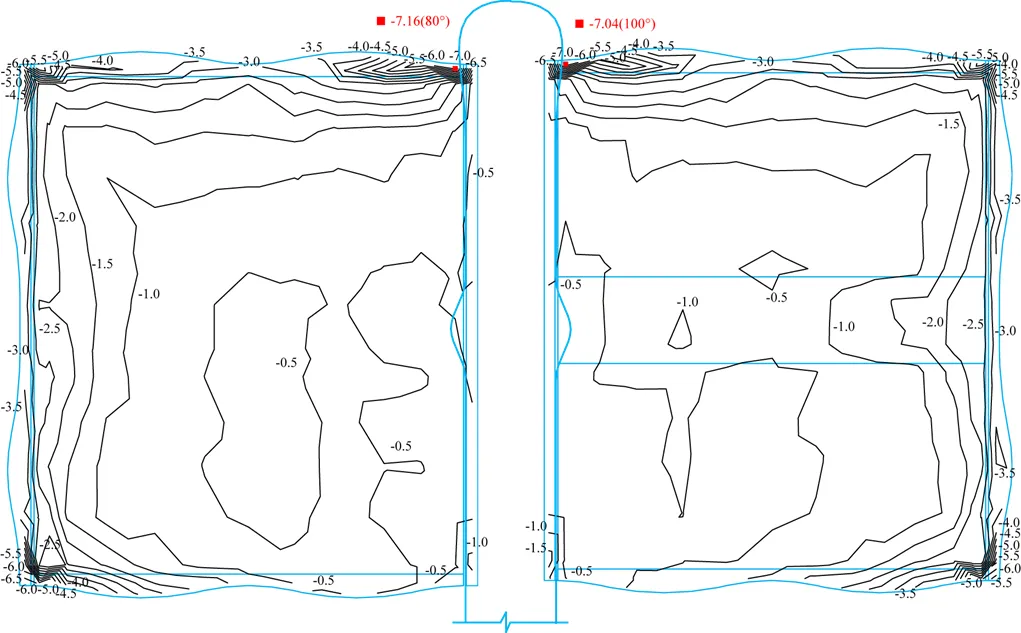
图6 全风向角极值负压分布图
由图6可以看出,两屋盖极值负压分布整体对称性较好,在屋盖中间开敞区域有些许差异。屋盖迎风的边缘角区风压等值线密集,风压变化剧烈。在外挑檐南北四个角区风压大致在-4.5 kPa至-6.5 kPa范围内,而在与中央廊道交界的角区风压为-5.0 kPa至-7.0 kPa。最大负压均出现在中央廊道与屋盖交界区外侧,屋盖V在80°风向角达到最大值为-7.16 kPa,对应的屋盖G则在100°风向角达到最大值为-7.04 kPa。其他区域从外向里则由-3.5 kPa缓慢减少至-0.5 kPa,并且-0.5 kPa区域接近整个屋盖的1/3。
3.3 底部封闭和开敞屋盖体型系数对比分析
由于屋盖V和屋盖G的不同之处在于底部是否开敞与两者之间存在2.9 m的高差,选取屋面典型测点在迎风向时(V180°、G0°)上、下表面以及总表面体型系数为研究对象,从而明确底部封闭与开敞对屋盖风场的影响。在屋盖的外挑檐选取一组测点(由北向南测点编号为185-21),另一组测点则在开敞区域的迎风向(测点编号为111-123),具体测点位置及编号见图3。图7和图8给出屋面两组测点迎风向的体型系数。
从图7可以看出,屋盖底部开敞后,外挑檐测点上表面负体型系数相比闭合屋盖均有不同程度的减小,开敞区域附近有微弱减小(风吸变小),远离开敞区域时则更显著。开敞区域内的测点110、95和靠近开敞区域的测点125、81下表面的正体型系数显著变大(风压变大),对于远离开敞区域的测点,两者下表面的体型系数基本一致。对于总体型系数,表现为屋面开敞后,外挑檐开敞区域附近风吸力变大,远离开敞区域时风吸力减小。
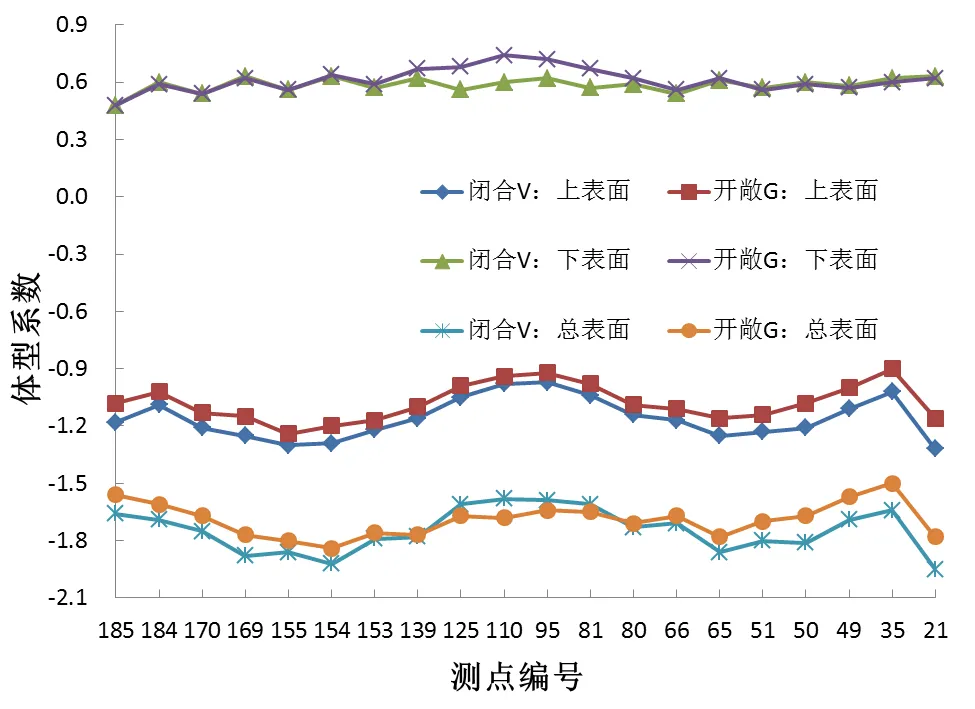
图7 外挑檐测点体型系数
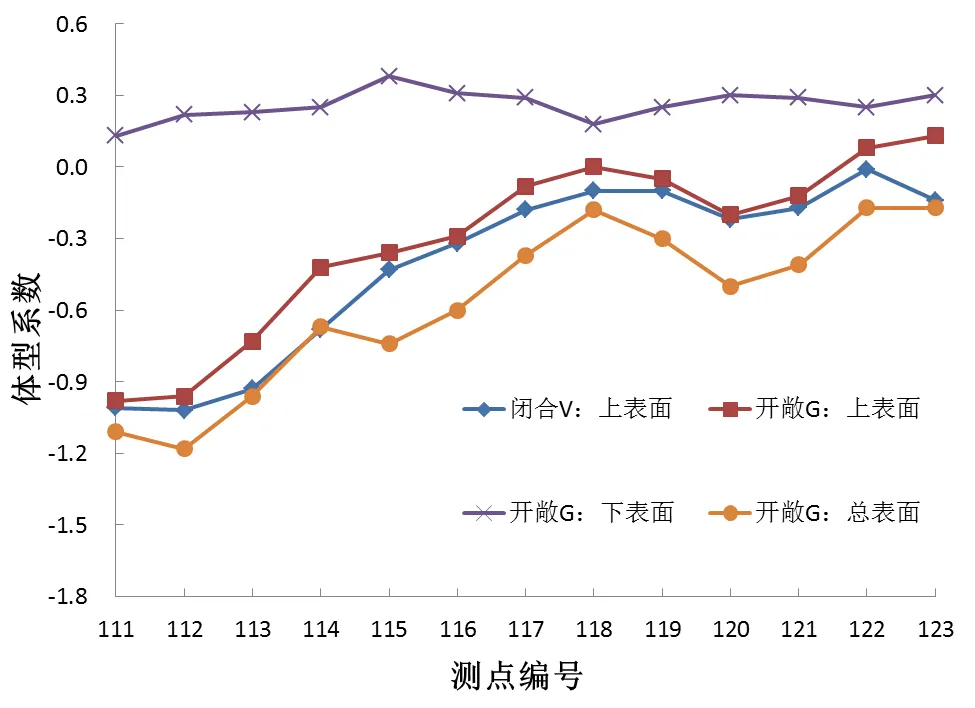
图8 开敞区测点体型系数
从图8可以看出,两个屋盖的上表面的风吸力随着距离的增加呈减小趋势,在波峰和波谷由于气流的分离再附会有所波动,而对于开敞区的下表面,体型系数曲线与屋盖的波浪形轮廓基本一样,波峰处风压较大,反之波谷处压力较小。开敞屋盖上表面负体型系数小于闭合屋盖,但是与下表面风压力相叠加后,屋面整体风吸力要强于封闭屋盖。
综合以上情况,屋盖底部开敞时,风加速从空隙流过,空隙之间的风由于汇聚效应导致开敞区域周围风荷载显著增大约6%,即“窄管效应”。而由于开敞区空隙的分流,减弱了钝体绕流的堵塞作用,使屋盖上表面风吸力有所减弱。
3.4 悬挑端体型系数分析
为了分析屋盖悬挑端的体型系数,图9分别给出屋盖V西侧、北侧以及屋盖G东侧、北侧悬挑区域测点在迎风向的体型系数。悬挑端具体测点的位置及编号见图3。
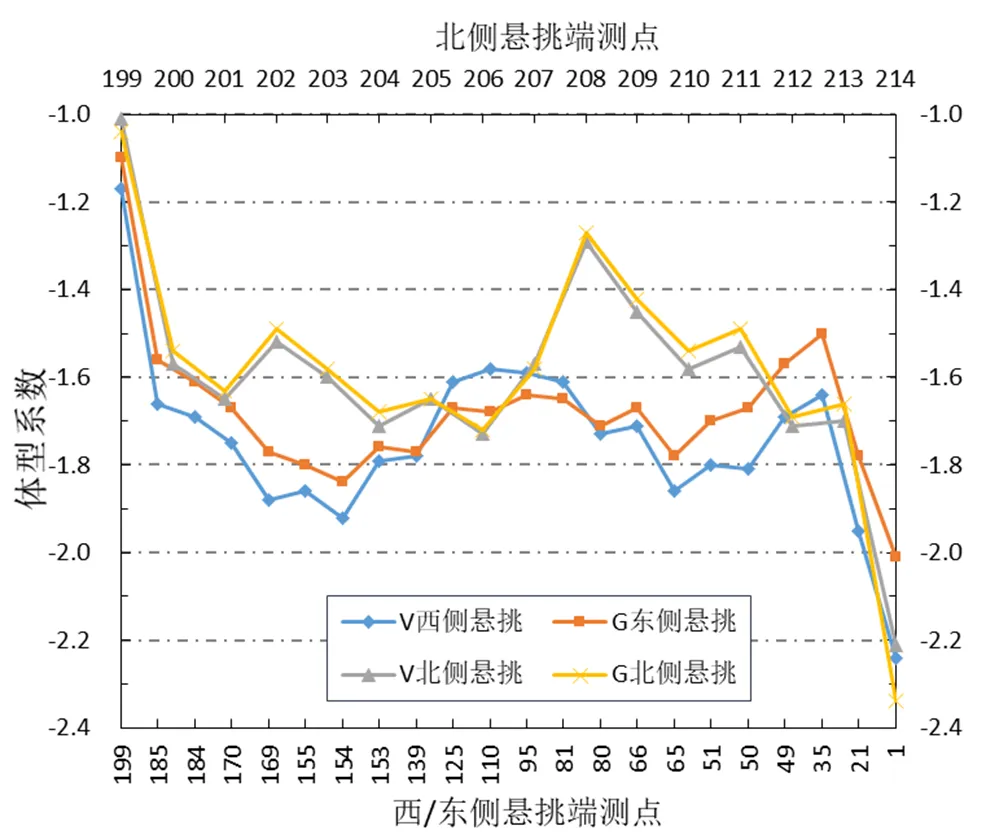
图9 悬挑端测点体型系数
由图9可知,屋盖V和G北侧悬挑端大部分测点体型系数在-1.5至-1.7区间,角区测点199和测点208的体型系数则较小。但测点214的体型系数却非常大,约为-2.3左右,此测点处于屋檐悬挑端的内凹拐角区且在中央廊道下面,当气流经过时,中央廊道阻挡了气流,形成自然的“风嘴”而产生“兜风效应”,显著放大了气流[8],使得这些部位所受的风荷载较大,在实际工程中需特别注意这种类似区域的抗风设计。屋盖东、西侧悬挑区域体型系数差别已在3.3节中介绍,此处仅对底部封闭屋盖进行分析。由图可知,角区测点199和测点1体型系数分别为-1.1和-2.0,而其他测点的体型系数基本在-1.6至-1.8区间。故对于此工程,屋盖悬挑端迎风向的体型系数可取为-1.5至-1.8,在局部凹角处和角区可放大约25%。
4 结论
1)屋面平均风压以负压为主,在迎风向屋檐及其角区出现明显的气流分离,存在很大的负风压且变化梯度很大;除屋檐悬挑区域附近外,屋盖其他区域风压较小。
2)结构外形在钝体绕流中起决定性作用,在某些风向角下,屋檐悬挑的凹角处由于结构局部特殊的体型产生“兜风效应”从而显著增大负压,需特别注意这种类似区域的抗风设计。
3)由于“窄管效应”,底部开敞屋盖在开敞区域周围风吸力增大,而底部开敞减弱了气流的堵塞作用,使屋盖上表面风吸力有所减弱,对下表面风压力影响不大。
4)对于本工程,屋盖悬挑端迎风向的体型系数基本在-1.5至-1.8之间,在局部凹角处和角区需适当放大。
[1] Holmes J D. Wind load of structures[M].New York:Spon Press,2001:210-221.
[2] 李方慧,倪振华,沈世钊. 不同地貌下几个典型屋盖的风压特性[J].建筑结构学报,2007(1):119-124.
[3] 董欣,叶继红. 大跨度平屋盖表面风荷载体型系数研究[J].土木工程学报,2012,45(4):29-42.
[4] 李元齐,胡渭雄,王磊. 大跨度空间结构典型形体风压分布风洞试验研究现状[J]. 空气动力学学报, 2010(1): 32-38.
[5] GB50009—2012 建筑结构荷载规范[S]. 北京:中国建筑工业出版社,2012.
[6] Davenport A G. Note on the distribution of the largest value of a random function witn application to gust loading [J].Proceedings of the Institution of Civil Enigineers,1964,28(2):187-196.
[7] 程志军,楼文娟,孙炳楠,等. 屋面风荷载及风致破坏机理[J]. 建筑结构学报, 2000(4): 39-47.
[8] 方江生,丁洁民,王田友. 北大体育馆屋盖的风荷载及周边建筑干扰影响的试验研究[J]. 空气动力学学报, 2007(4): 443-448.
Wind Tunnel Test of A Convention and Exhibition Center
*LIU Biao1, HUANG Yong-jun2
(1. School of Civil Engineering and Transportation, South China University of Technology, Guangzhou, Guangdong 510641, China;2. Shenzhen Aube Engineering Architectural Design Co., Ltd., Shenzhen, Guangdong 518053, China)
Based on the wind tunnel test of two long-span waviness cantilevered roofs on the north of a convention center,the mean wind pressure distribution under typical wind direction is discussed. Moreover,the distribution of mean wind pressure, fluctuating wind pressure and extreme wind pressure under the full wind direction are studied.Furthermore,the effect of open bottom on the wind load of cantilevered roof is discussed. The test results show that the roof is mainly presenting negative pressure, and the wind pressure in other areas is very small except for the cantilevered area of the roof under the windward direction. The special shape of the roof may cause “catch the wind” to increase the wind pressure significantly and the “narrow tube effect” caused by the open bottom will increases the wind load in the open area significantly. Meanwhile,since the open bottom weakens the blockage of the airflow, the wind suction on the upper surface of the roof is weakened, but the wind pressure on the lower surface is not greatly affected.The shape coefficient of the cantilevered area of the roof in the windward direction is approximately in the range of -1.5 to -1.8.
long-span cantilevered roof; wind tunnel test; wind pressure coefficient; shape coefficient
TU312.1
A
10.3969/j.issn.1674-8085.2019.02.014
1674-8085(2019)02-0077-06
2018-12-29;
2019-01-14
*刘 彪(1994-),男,江西吉安人,硕士生,主要从事结构工程抗风研究(E-mail:liubiao1102@163.com);
黄用军(1962-),男,湖北武汉人,教授级高级工程师,主要从事结构设计工作(E-mail:huangyongjun@aube-cc.com).

