《周髀算经》“周公商高问答”相关问题的研究

俞求是

(教育部人民教育出版社中学数学室 100081)

《周髀算经》是我国最早的数学典籍，是研究中国数学史的重要文献，其中第一篇“周公商高问答”对于研究勾股定理具有重要价值，引起了研究者的重视.由于教材工作的原因，我近期研读了《周髀算经》及部分研究文献，感到准确估计和确定中国数学史中勾股定理的发现和证明的时间等问题很重要，很值得研究，这些问题的研究对于相关内容的教学也有一定的参考价值.

1 “周公商高问答”原文

要论述有关问题，先陈述“周公商高问答”原文如下(原文是繁体字，现改用相应简体字叙述)：

昔者周公问于商高曰：“窃闻乎大夫善数也，请問古者包犧立周天历度，夫天不可阶而升，地不可得尺寸而度，请问数安从出？”商高曰：“数之法，出于圆方，圆出于方，方出于矩，矩出于九九八十一.故折矩，以为勾广三，股修四，径隅五.既方之外，半其一矩，环而共盘，得成三四五，两矩共长二十有五，是谓积矩.故禹之所以治天下者，此数之所生也.”周公曰：“大哉言数.请问用矩之道？”商高曰：“平矩以正绳，偃矩以望高，覆矩以测深，卧矩以知远，环矩以为圆，合矩以为方.方属地，圆属天，天圆地方.方数为典，以方出圆.笠以写天，天青黑，地黃赤.天数之为笠也，青黑为表，丹黃为里，以象天地之位.是故，知地者智，知天者圣.智出于勾，勾出于矩.夫矩之于数，其裁制万物，惟所为耳”.周公曰：“善哉！”

2 “周公商高问答”的解读

为了理解以上对话，先对其中的一些人物和词句作注解和分析如下.

周公，姓姬名旦，为周武王之弟，周成王之叔.周武王死后，周成王年幼，周公摄政，多有建树.周公对于中国周代及后续时期的文化传统产生重要影响.

文中“昔者”一词说明，《周髀算经》写作年代晚于周公、商高的时代.“商高与周公对话的时间已无可稽考，但周公去世之年已确知为公元前1105年[1].《周髀算经》原称《周髀》，是一部以“盖天说”宇宙模型为中心的天文学著作，其中用到了许多数学知识，所以也是一本数学著作.此书作者不详，成书年代据考为西汉(前206—公元25)初[2].从数学上看，《周髀算经》)主要的成就是分数运算、勾股定理及其在天文测量中的应用.所谓盖天说，是中国古代一种宇宙模型，认为“天象盖笠，地似覆槃”[3].

商高，其生平未详，赵爽注：“商高，周时贤大夫，善算者也.”西北大学李继闵教授在“‘商高定理’辩证”一文中对于商高的生平作了详尽的考证[4].

包犧，传说中远古的三皇之一，也写作伏羲、庖牺、包牺.《易·系辞下》：“古者包牺氏之王天下，仰则观象于天，俯则观法于地.”相传八卦由他所创，近年国内的一些考古研究支持以上观点.立周天历度，建立周天测量度数，建立古代历法.这里的周天，估计用于时间或空间测量.

矩，又称曲尺，L型的木匠工具.古代“矩”指L型曲尺，由长短两根木条组成的直角(在两条边上也可按用途取相等之值)，短边称为勾，长边称为股.“矩形”是“矩”衍生的长方形.“矩”在商高时代有多种含义，除了曲尺、直角之外，矩有时也指正方形和长方形的面积.

圆出于方，求圆的方法可由方的数理特性推导.赵爽注：“方，周匝也.”引申为多边形的周长.商高时代中国古代数学已创建出一个推算圆面积的方法，其步骤是“毁方而为圆，破圆而为方.”[3]

方出于矩，方的运算方法可由矩的直角特性推导.古文“方”指正方、长方且有直角的含义[3],如“合矩以为方”，意思是指把两个矩尺以适当的方式合摆成正方形或长方形.

“九九八十一”指乘法运算，古代常以特例作名.如“九九”是中国古代对于乘法口诀的称谓.中国古代的乘法口诀是从“九九八十一”开始的，所以称为“九九”，到宋、元时，九九乘法口诀的次序才颠倒过来从“一一得一”开始[3].

故折矩，以为勾广三，股修四，径隅五.赵爽注：“故者，申事之辞也”.折矩，将矩形沿对角线一折为二，得两个全等的直角三角形.勾广三，赵爽注：“应圆之周，横者谓之广，勾亦广.广，短也.”股修四，赵爽注：“应方之匝，从者谓之修，股亦修.修，长也.”径隅五，赵爽注：“径，直；隅，角也.亦谓之弦.”这里的径，指直角三角形的斜边.整句意思是，如果勾为三，股为四，那么径就是五.

由于断句的不同,对于关键句子“既方之外，半其一矩，环而共盘，得成三四五，两矩共长二十有五，是谓积矩”有不同的解读.例如，李继闵教授认为，此处原文是：“既方之，外半其一矩，环而共盘，得成三四五，两矩共长二十有五，是谓积矩.”并对原文图示(商高勾股图一，见图1)如下[4]：

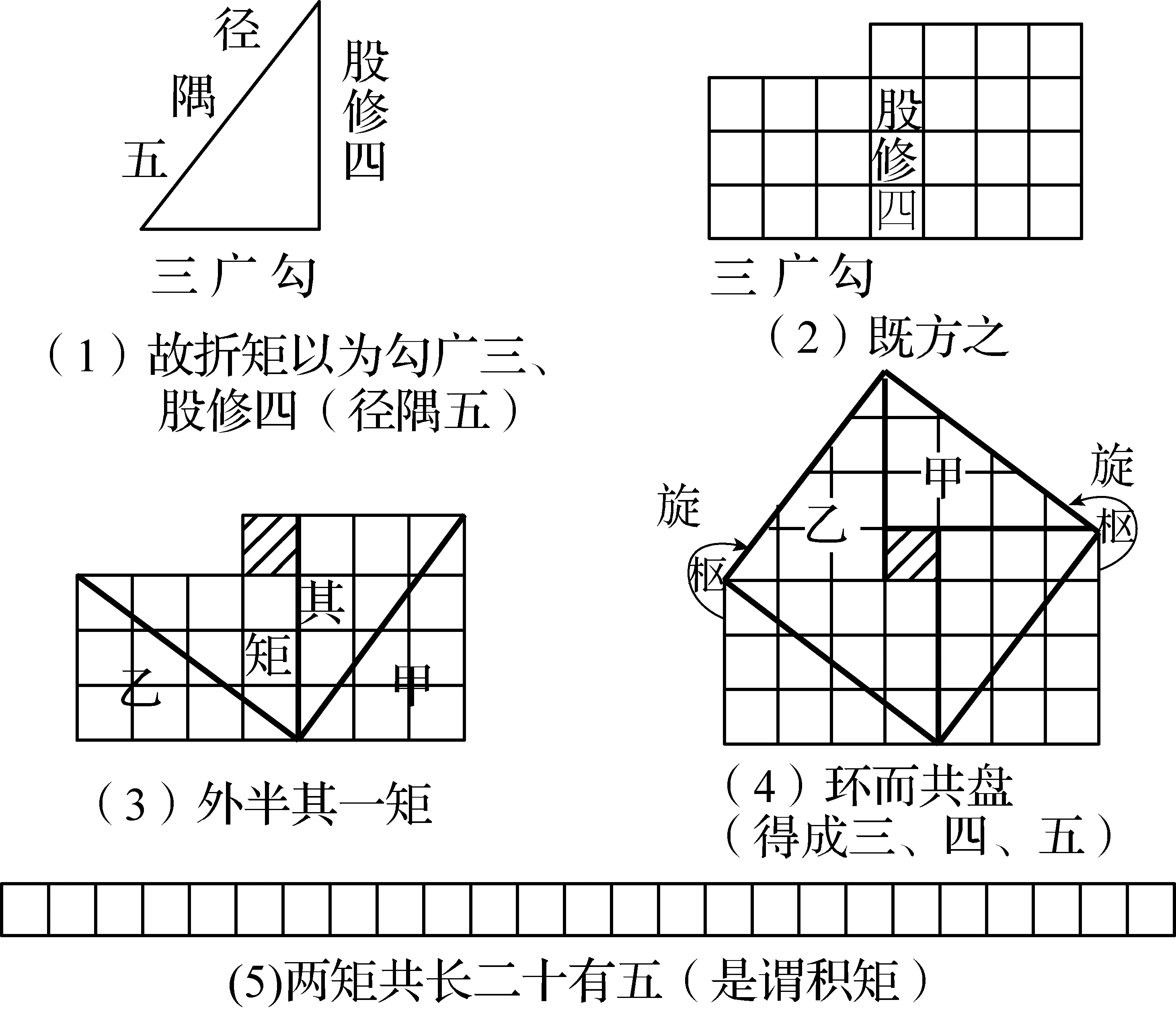
图1

再如，美国科学院院士程贞一教授认为：原文开头一句是：“既方之外，半其一矩”，“既方之外”是指在勾股形之外以径(斜边)为边作正方形；“半其一矩”指取半个长方形.“环而共盘”指环绕正方形一周，共同组成一方盘(见图2)，并称所得的图为“商高勾股图二”.“如此所得之大方弦图，正是赵爽弦图的外弦图(见图3).”“得成三四五”：得以推出勾股定理[3].

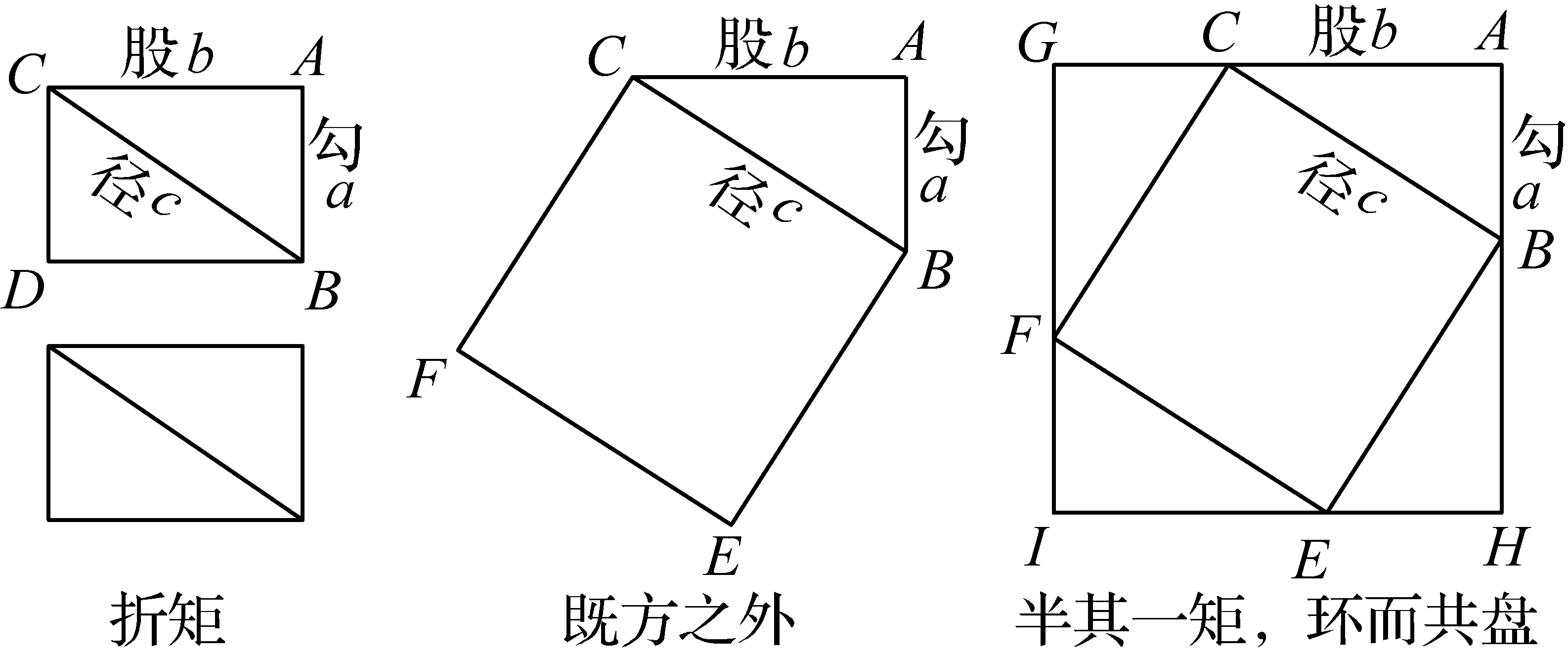
图2

图3

对于“两矩共长二十有五，是谓积矩.”赵爽注：“两矩者，勾股各自乘之实，共长者，并实之数.”由此注理解：“两矩共长二十有五”即勾方和股方两个矩形面积之和二十有五，也就是径方的面积.即：

勾方+股方=径方.

这就是勾股定理.

无论对《周髀算经》此段原文如何理解，这段文字都是说勾股定理的推导[3].“积矩法”肯定是利用图形面积之间的关系来推证“勾股定理”的.

“故禹之所以治天下者，此数之所生也”，这也是非常关键的一句话.大禹治水十三年，三过家门而不入，大禹治水是中华民族远古时代的一件大事，治水成功的要旨是采用了疏导的方法，为此必须“望山川之形，定高下之势”.根据《史记·夏本纪》，大禹在治水时“左准绳，右规矩”，说明在治水中必须经常与直角打交道，经常要用圆规，用矩尺，这就为发现勾股定理提供了机会，在测量的实践中，大禹时代的人，也许大禹本人，已积累了不少数学知识，包括用矩的经验，为发现勾股弦关系打下了基础.据说大禹治水巡视到会稽(即现浙江绍兴)时因病而死，会稽山下的禹穴就是他的墓地，后人为了纪念他就在那里建立了禹陵碑和禹庙，这些古迹至今都保存着.大禹治水是不必怀疑的历史事件. 大禹治水的故事，以及相关的勾股定理知识是如何在古代流传下来的当然是另外的问题，文化具有代代相传的特点，没有非常特殊的外力破坏，重要的、优秀的文化积累一定会代代传承.唐代著名诗人李白也有诗句：“黄河西来决昆仑，咆哮万里触龙门.波涛天，尧咨嗟.大禹理百川，子啼不窥家.”国家的治理，治水是一件大事，古今中外都是如此. 1998年，多位中央领导亲临全国各地抗洪现场领导抗击特大洪水，抗洪救灾的干部、群众和人民解放军、武警官兵，日夜奋战终于保住长江大堤，否则将会造成极大的人员伤亡和财产损失，情况将不堪设想！我上中学时学校就多次组织学生参加水利基础工程建设劳动.赵爽有注：“禹治洪水，决流江河，望山川之形，定高下之势，除滔天之灾，释昏垫之厄，使东注于海而无浸逆.乃勾股之所由生也.”李继闵教授认为：“中国古代以勾股定理为基础的勾股术无疑产生于窥天测地.《史记·夏本纪》：‘(禹)陆行乘车，水行乘船，泥行乘橇，山行乘檋.左准绳，右规矩，载四时，以开九州，通九道.’足见大禹治水使用规矩进行测绘之说流传久远”，“此数指勾股之数‘三、四、五’，也泛指勾股定理所表的数量关系，依商高所说，大禹治水得力于勾股术的应用.”，可见，人们对于“故禹之所以治天下者，此数之所生也.”这句话的理解有两种：第一种，勾股定理(或其特例)产生于大禹治水(公元前21世纪)的过程中，赵爽注似乎更接近这个观点；第二种，大禹治水的许多办法是根据勾股定理(或其特例)而得到的.两者必居其一.如果按照第二种理解，勾股定理的发现可能比大禹治水的时间还要早.无论怎样去理解，都可以推知，大禹治水时人们一定已经知道“勾三股四弦五”的特殊结论，还有可能知道勾股定理的一般结论.

根据世界数学史的普遍规律，许多数学知识，尤其是几何知识，往往产生于在洪水泛滥以后各地土地划分整治的过程中.在中华大地上，许多数学知识，特别像勾股定理一般结论或者特殊结论的几何知识也会产生于治理大自然的过程中的观点还是比较可信的，比较符合数学发展的普遍规律.所以，不管“故禹之所以治天下者，此数之所生也.”这句话应该怎样去理解，可以相信，在中国，勾股定理(或其特例)也是产生于像大禹治水这样的生产活动过程中，或者就直接产生于大禹治水的过程中，也就是说，在大禹治水的过程中或者更早的类似活动中，人们就已经发现了勾股定理的一般结论，或者，发现了“勾三股四弦五”的特殊结论，两者必居其一.

至此，似乎可以断定一些结论了.但是，从逻辑严密要求出发，数学史专家们认为仍有漏洞.“《周髀》所引商高和陈子的话及禹之治天下为数之所由生是真有其事，还有假托，无法确定.这就牵涉到像勾股定理这样重要数学成果的获得年代问题.这条定理肯定不会是在西汉时期突然出现的，必然有一个相当长的发展过程.”[5]以上论述中提出的疑问有所谓疑古主义的倾向，从逻辑上来说提出的疑问是无可厚非的，凭《周髀算经》一家之言，缺乏考古学、历史学严密的论证，结论确实还不足以确立.不过，另一方面，《周髀算经》以后并没有另外典籍去批驳此书的记载，所以，根据《周髀算经》的记述推断出大禹治水时期就已经发现勾股定理的特例结论，或者已经发现勾股定理的一般结论，既还不能完全肯定，也还无法否定，基本上是可信的. 对照世界数学史的类似情况，我认为可以有很大把握作出一个判断：在古代中国，至迟在大禹治水时期人们就已经知道勾股定理“勾三股四弦五”的特例结论，或者直接知道勾股定理一般结论；另外，由于《周髀算经》周公与商高的对话中已经记录下定理证明方法，我国古代证明勾股定理的最晚时间肯定不会晚于《周髀算经》写作的时间，后来赵爽在为此书作注时作“勾股圆方图”对定理给出了图解.

商高曰：“平矩以正绳，偃矩以望高，……”这一段话，前一部分回答周公用矩之道的问题，后一部分主要是所谓“盖天说”的一段论述，与勾股定理联系较弱.

参考程贞一教授《〈周髀算經〉译注》一书，我尝试用意译方法作出对“周公商高问答”的今译：

从前，周公问算数于商高说：“我早已听说大夫您是位擅长于数学的人.请问古时伏羲建立周天测量度数，可是天没有台阶可供攀登，地也不适合以尺去度量尺寸，请问这些数是从何处得来的？”商高说：“数学的方法出于圆和方的数理特性.圆可由方的数理特性推导，方可由矩的直角数理特性推导，矩的数理原理出于乘法法则.所以，将矩形沿对角线一折为二得两个相等的直角三角形，那么，勾方加股方就等于径方.例如，如果勾(即短边)等于三，股(即长边)等于四，那么所得直角三角形的径(即弦，斜边之长)就等于五(这三四五这三个数按九九表来计算有三三加四四等于五五的关系).为什么呢？您看，在直角三角形之外，以径(斜边)为边作正方形，然后每次取半个矩形，四次就可以环绕正方形一周，这就形成一个大的方盘了.由此推导，就可以得出成立“三四五”的数理关系了.因为由构图得，由两个矩形分成的四个直角三角形围成的径方的面积等于大的方盘面积(七七四十九)减去两个矩形的面积(三四一十二的两倍二十四)，从而推导得径方面积等于二十五，这恰好等于勾方的面积九加股方的面积十六，得到径等于五，这就是所说的勾三股四径五.这种推导法就是所谓的‘积矩’法.大禹之所以能够(由治水而)治天下，就得力于以上的数量关系(这句，也许另一种理解：以上的数量关系来自于大禹(治水而)治天下的过程中，不过，这样理解，之所以三字似乎讲不通).”周公说：“照你这么说，研究数学其意义可是相当重要！那我再向你请教一下用矩的方法.”商高答道：“您看，利用矩的直角边和重垂线，可确定水平面.把矩仰立放，可测高度.把矩倒置，可测深度.把矩卧放与地面平行，可测水平距离的长度.把矩环旋一周，可以得到圆形.将两矩相合，可得方形.方的数理应用于观测地，圆的数理应用于观测天，人们常说天圆地方.以方的数理为基础，以处理方的方法推导出圆之数理.笠可用来写意天的功能与表现天的形态.天色青黑，地色黄赤.以笠来写意天的数理特质，天色青黑为其外表，地色黄赤为其里面,用来象征天地方位.所以说，通晓地上事物的是智者，理解天上事物的是圣人.智出自善于设勾测量的才华，把矩固定作表，可以测量出勾影.矩对于算数应用的重要性，在于测算制作万物，用起来得心应手.”周公说：“好极了！”

3 相关问题的研究

从“商高曰：数之法，出于圆方，圆出于方，方出于矩，矩出于九九八十一.”可以看出，在商高看来，数学知识之间并非互相孤立、互不相干，而是存在密切关系，从一些基本事实、基本结论出发，可以推出复杂图形的性质.在以上叙述看，最基本的根据是“九九八十一”，是算术基本知识.矩的有关计算就是用自然数的乘法法则.由此看来，在数学中应用逻辑推理是古代中国很早就有的事情了，这是很了不起的.另外，上面“圆出于方，方出于矩，矩出于九九八十一”中的圆、方、矩等显然是极简的表达，可以肯定，它们代表了相应图形一系列几何性质.由此可以推断，在中国，早在商高时代甚至远在商高时代之前，人们就已经专门研究了这些图形的几何性质.

程贞一教授有一个重要观点：这里的“三四五”是指直角三角形勾、股和径(即弦)的数理关系，即现称的勾股定理，这是商高篇中以特例为名的又一实例[3].可以想象，古时表述数量关系缺乏一套简便的符号、语言体系，所以用“勾、股、弦”表达直角三角形的三条边，以3，4，5之间所具有的平方关系代表勾股弦的一般关系，这是极简的叙述.勾、股、弦的关系当然并不限于整数，推导方法也可推广，用“三四五”的名称清楚说明了图形性质.

另外，商高在将矩形沿对角线一折为二得两个相等的直角三角形(折矩)之初，并不要求此矩形的短边和长边分别等于3和4，也许能说明，他对于矩形的选择是随意的.为了能够更简明地给周公说清道理，便先选择了“三四五”特例，这是很高超的.商高既知道一般结论，又熟悉特殊结论.

历史上，是先发现勾股定理“三四五”特例，还是先发现勾股定理一般结论，是一个值得研究思考的问题.这个时间顺序依赖于发现勾股定理的具体情境和途径.当然只有两种可能，一是先现特例再发现一般结论，另一种是先发现一般结论，再发现特殊结论.可以设想古人研究过程中的可能情境.有一种情境可能是研究是否存在三条整数边长的直角三角形，这是容易通过试验得到一些猜想的命题，当排除一些容易排除的特殊情况以后，就得到一个了猜想：一个直角三角形两直角边的长分别为三和四，其斜边长极可能就等于五.一个新问题就摆在面前了！这个问题只依靠简单的长度或者角度的测量都是不能说明问题的.于是，人们可能想到了一个极妙的办法，就是把问题转化为等价的一个问题，把长度测量的困难问题转化成面积关系的探究，这是极其重要而极巧妙的想法.要证明某边长是5，只要证明某正方形的面积等于25！而这是可以借助图形之间关系来加以说明的！(这里也许说明了人们为什么想到通常用面积去证明勾股定理，勾股定理可是关于边长的结论啊！).也许人们曾经同时研究过两个问题：三边长分别为三、四、五的三角形是直角三角形吗？如果一个直角三角形两条直角边的长分别为三和四，第三边的长是五吗？根据初等几何理论可知，从逻辑关系去分析，这是两个完全等价的命题.于是，问题可以归结为研究：如果一个直角三角形两直角边的长分别为三和四，斜边长是五吗？又转化等价命题为：如果一个直角三角形两直角边的长分别为三和四，以斜边为边的正方形的面积是二十五吗？经过研究可以得到结论，存在三边长分别为三四五的直角三角形.通常人们说“勾三股四弦五”，其实这究竟指什么具体的数学命题是有些含糊的，显然有一种理解就是：存在三边长分别为三四五(勾三股四弦五)的直角三角形.应该注意，这个结论还不是勾股定理的特殊情况，因为勾股定理指出的是边长的平方关系.也许经过很长时期，人们又发现了3，4，5这三个数之间的平方关系，于是就得到了勾股定理的特例了.由于平方关系从几何上看是面积关系，这种关系对一般直角三角形也可以同样推证出来，于是就得到了一般形式的结论.如果历史上是按照这样的路径和顺序发现了特殊结论和一般结论，那么，这两个结论的发现时间间隔应该不会很长，而且，特殊结论先于一般结论被发现.在中学数学教学中，或者在数学史的研究中常常认为勾股定理特殊结论“勾三股四弦五”(此处指存在边的平方关系)和一般定理这两个结论是先后独立发现的.究竟这两个结论是独立地有先后地出现在数学历史中，还是基本同时被发现的呢？这当然是值得思考的一个问题.进一步的思考，应该可以得到判断：“勾三股四弦五”的特殊结论应该不会与勾股定理一般结论相差很长时间得到.因为，“勾三股四弦五”特殊结论离开了一般结论基本上是不能立足的.没有一般结论的观念，大概也不会有特殊结论的观念.如前所述，也许人们曾经研究过是否存在三边都是整数边长的直角三角形的问题，由于测量精度原因，不能从一个直角三角形有两边分别是三和四，通过测量确认另一条边就是五，因为测量存在误差问题.也许正是这个原因，并发现3，4，5三个数之间特殊的平方关系，人们猜想到一般结论.当然，从猜想到证明一般结论，应该需要一段时间.不过，如果想到了面积方法，大概证明就很快可以得到了，到现代，人们对于勾股定理，已经有几百种证明方法了，在这些方法中发现几种证明方法并非难事！所以，可以认为，从猜想有“勾三股四弦五”边长平方关系结论，到得到勾股定理一般结论，时间不会太长；或者相反的方向，有了一般结论，另加一个边长是整数的特殊要求，也就很快能够得到特殊结论.从数学史几千年这么大的时间跨度来看，可以认为，一般结论和特殊结论应该是几乎同时得到的.这个基本而重要的几何结论的发现确实是应该好好庆祝一下的，无论是在中国，还是在希腊，都可列入重大科学发现，这么基本，这么美妙！三四五，太美妙了！也许当时还没有太好的命名方法去称呼这个结论，那就把这个结论简称为“三四五”吧！这样称呼也挺好！

此外，程贞一教授认为：“商高积矩推导法的一个主要成就是把数学由经验层次发展为推导证明的层次，从而奠定了中国理论数学的基石.”“商高所叙述的证明勾股定理的方法是世界数学史现存最早证明勾股定理的记载.”“这些成就奠定了《商高篇》在世界数学史应有的地位.”[3]他的观点具有重要意义.

对于毕达哥位斯学派怎样发现定理的，目前普遍认为是毕达哥位斯学派甚至也许是毕达哥拉斯本人在研究地砖图案中的面积关系时，先发现了等腰直角三角形的特殊情形下的勾股定理结论，进而研究一般情形下的结论，导致定理的发现.这是一个比较符合逻辑的过程.也是目前多数中学数学教科书中引入的情境.从教学的角度来说，确实是可以接受的一种设计.不过，数学史的考证研究是另外一会事.实际上，许多研究者认为，毕达哥拉斯学派是否真正发现并证明了勾股定理本身并没有确凿的证据.

4 主要结论

综合本文以上分析，我们有很大的把握得出以下主要结论：

(1)在我国，早在大禹治水时期(公元前21世纪)或者更早，人们就已经发现了(此处发现指已经能够推理论证)一般形式的勾股定理，同时也发现了(此处发现也指已经能够推理论证)“勾三股四弦五”特例结论，并把结论用到生产实践之中；在中国最早有文字记录与勾股定理有关的历史人物是大禹.时间远早于毕达哥拉斯(约公元前6世纪)；

(2)到西周的周公时(约公元前1100年左右)，数学家商高不但能够清晰地说明勾股定理，而且能极清晰地用“勾三股四弦五”的特例来讲述一般数量关系，能够用积矩法证明勾股定理的一般结论，这是中国有文字记载的最早的勾股定理证明方法.这一时间也远早于毕达哥拉斯(约公元前6世纪),但商高不是最早得到勾股定理的中国人；

(3)在我国，最迟到《周髀算经》成书的时代，即不晚于西汉时期(从公元前206年到公元25年)，《周髀算经》记录了推证勾股定理的思想方法；

(4)在我国，到三国时吴国人赵爽在约公元222年前后为《周髀算经》作注时，作“勾股圆方图”，画出了前人证明勾股定理的图形，并给出了新的证法.赵爽的证法是极直观而简捷的.