混凝土管端口打磨机器人设计及力学性能分析

崔国华 刘 健 马 良 崔康康

1.河北工程大学机械与装备工程学院，邯郸，056038 2.河北工程大学材料工程学院，邯郸，056038

0 引言

预应力钢筒混凝土管道以其高密封性、高强度和高抗渗的特性，得到日益广泛的工程应用[1]。管芯制作过程中，其承口、插口会附着较多的混凝土和砂浆，需要对管口部位进行打磨清理[2-3]。目前，一般采用人工打磨，效率低下、质量较差、工作环境恶劣，无法满足较大口径管道的打磨需求。已投入应用的自动化管口打磨装备[4]虽提高了打磨效率，但设备过于巨大，且需一台大型起重机辅助作业，不能满足多样化产品现场需求。

文献[5-7]针对小口径管道工作的小型机器人进行构型与结构设计，此类机器人可携带特殊设备，完成小口径管道内部的打磨、检测等工作。文献[8-11]设计了几种针对较大口径管道的打磨机器人，此类机器人可在管道内部行进，完成打磨工作。文献[12-14]设计了适用于复杂曲面的打磨机构，通过工业串联机器人的带动来完成打磨任务。但上述打磨机器人均不能满足大型预应力钢筒混凝土管道管口磨机的任务需求。

本文通过对预应力钢筒混凝土管道管口打磨任务的分析，设计了一种新型便携式管口打磨机器人用于管道插口端打磨，基于构型演变法[15]完成其构型设计及结构设计，建立力学模型并求解了其工作时的最危险载荷。有限元仿真分析和现场样机试验验证了该打磨机器人结构安全稳定，具有较高的打磨效率和打磨质量。

1 机器人构型与结构设计

1.1 构型设计

根据对预应力钢筒混凝土管道管口打磨的功能任务需求分析可知，该类打磨装备有两种设计方案：①打磨装备固定，管道自身旋转进行打磨；②管道固定，打磨装备绕管道端口旋转打磨。在上述方案中，方案①所需电机功率极大，打磨装备的体积与质量相对变大，不符合要求，因此选用方案②。

在对方案②进行分析的基础上，笔者提出一种自行走式管口打磨机器人设计方案，其基本构型如图1所示。该机器人主要由行走机构、夹持机构、末端执行打磨机构组成。行走机构主要由行走支架、行走轮及驱动电机组成，行走支架上侧用移动副与夹持机构的支架连接。通过调节上侧移动副，使行走轮配合夹持支架的2个夹持臂夹紧管壁，由电机驱动的行走轮可带动打磨机器人绕管道端口行进。末端执行打磨机构的支架与夹持支架同样由移动副连接，以调节打磨头位置，适应不同口径管口。

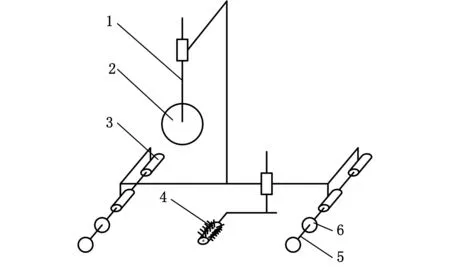
1.行走支架 2.行走轮 3.轴承座 4.钢丝刷 5.夹持臂 6.从动钢轮图1 打磨机器人基本构型图Fig.1 Basic configuration of grinding robot

1.2 结构设计

以上述构型为基础，对该类机器人进行结构设计。由于预应力钢筒混凝土管插口端与承口端管口结构不同[3]，因此设计了2种管口打磨机器人以应对不同的打磨需求。本文仅对插口端打磨机器人(图2)进行结构设计及分析，行走轮及驱动电机由链条连接并固定在行走支架上，夹持支架的2个夹持臂上分别有2个窄钢轮，外侧钢轮可放进插口端管口的密封槽，上侧钢丝拉紧器拉紧后，驱动电机可带动整个打磨机器人绕管口行进，通过调节末端执行打磨机构上的螺杆控制打磨力度。此设计有效减小了打磨设备的体积，该打磨机器人在安装后可自行运行，其夹持机构夹紧方式为纯机械式夹紧，安全可靠，适应现场复杂的环境。

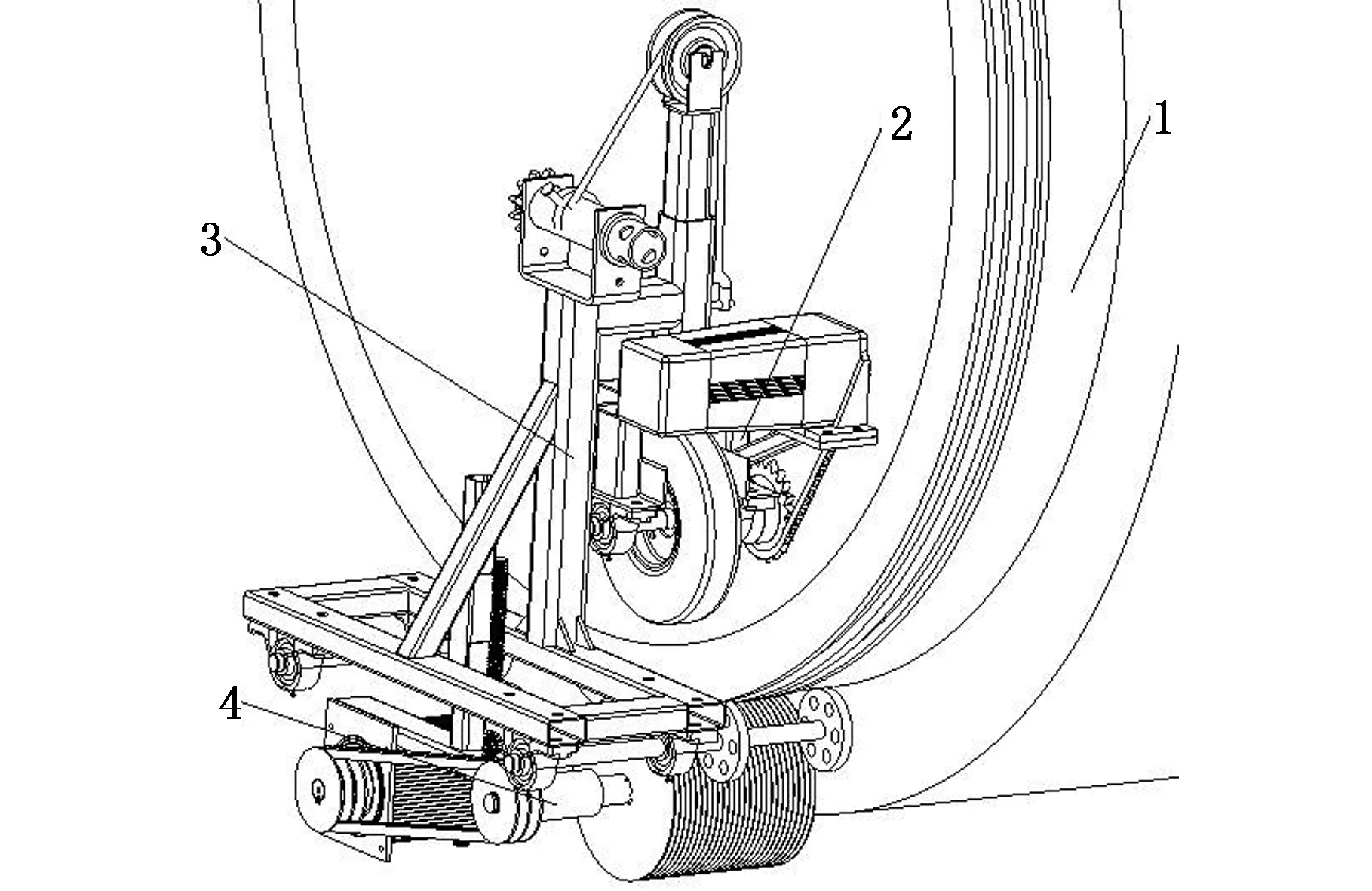
1.插口端管口 2.行走机构 3.夹持机构 4.末端执行打磨机构图2 插口端打磨机器人结构模型Fig.2 Structural model of jack end grinding robot

2 力学分析及载荷的确定

2.1 力学模型

驱动电机转速恒定，因此打磨机器人的运行可看作是竖直面内的匀速圆周运动，且由于其行进速度较慢，故可忽略其向心加速度。打磨机器人绕管口逆时针打磨一圈受力状况可等价为：在其自身坐标系内，重力绕其质心Q在OXY平面顺时针旋转一周，其他力的方向均不发生变化。

图3为根据插口端打磨机器人的运动原理作出的运动机构受力简图，其中，N1为管口对行走轮的支持力；N2为管口对钢丝刷的支持力；Ni(i=3，4，5，6)为管口对各从动钢轮的支持力；f1为行走轮所受摩擦力；f2为钢丝刷所受摩擦力；fi(i=3，4，5，6)为各从动钢轮所受摩擦力；G为机器人重力；φ为重力G在机器人自身坐标系下与Y轴负方向夹角，φ∈[0, 2π]；θ为从动钢轮所受支持力Ni在机器人自身坐标系下与Y轴负方向夹角；C1D1=C2D2=h，C3D3=H，D1E=ED2=L，SE=2L，KM=l，A1B1=A2B2=A3B3=KS=2d，B1C1=B2C2=d。

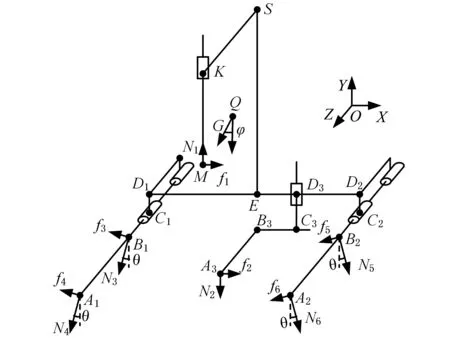
图3 打磨机器人机构受力简图Fig.3 Force diagram of grinding robot mechanism

2.2 打磨机器人工作状态下的受力分析

以上述力学模型为基础，对插口端打磨机器人进行受力分析。为方便计算，认为质心Q在MKS平面内，且Q到KM的距离为d，到KS的距离为l。

根据空间力系平衡条件得到：

X方向的受力平衡方程

N1=N2+Gcosφ+(N3+N4+N5+N6)cosθ+

(-f3-f4+f5+f6)sinθ

(1)

Y方向的受力平衡方程

f1=-f2+Gsinφ+(N3+N4-N5-N6)sinθ+

(f3+f4+f5+f6)cosθ

(2)

绕X轴的扭矩平衡方程

f2(2L-l+H)=(-N3-N4+N5+N6)·

(Rcosθ-2L+l-h)sinθ+(f3+f4+f5+f6)·

[R-(Rcosθ-2L+l-h)cosθ]

(3)

绕Y轴的扭矩平衡方程

N1d=N2d+2(N4+N6)dcosθ+

2(-f4+f6)dsinθ

(4)

绕Z轴的扭矩平衡方程

f1d=-f2d+2(N4-N6)dsinθ+

2(f4+f6)dcosθ

(5)

fi=μNi

(6)

f2=9550P/(nr)

(7)

式中，R为管口内径；μ为钢轮与管口钢圈的滚动摩擦因数；P为打磨伺服电机的功率，kW；n为伺服电机转速，r/min；r为钢丝刷半径，m。

θ、l、H会根据管口内径R的不同而发生改变。由于钢丝刷由大量钢丝编制而成，其径向受力后会产生较大变形量，因此可认为N2在运动过程中大小恒定。

设备运行时需要有一个预夹紧力来使设备抓紧管口，防止滑落，预夹紧力方程为

Ft=(N3+N4+N5+N6)cosθ+N2+

(-f3-f4+f5+f6)sinθ

(8)

联立式(1)～式(5)、式(8)可解得

N1=Gcosφ+Ft

(9)

f1=Gsinφ-f2+μ(Ft-N2)-

(10)

δ1=Rcosθ-2L+l-h

(11)

δ2=2L-l+H

(12)

两侧夹持臂上的合力分别为

(13)

(14)

由式(6)、式(11)～式(14)可知，夹持臂上所受合力为定值。

2.3 预压紧力参数选取及极限载荷的确定

打磨机器人在工作状态下有下滑的趋势，为使其不发生滑移情况，应有λN1≥|f1|，其中，λ为行走轮与管口内侧管壁的滑动摩擦因数。将式(9)、式(10)代入λN1≥|f1|可得

(15)

表1所示为打磨机器人的主要性能参数，将参数代入式(15)进行计算，可得Ft≥1158.7N。

表1 打磨机器人主要性能参数

取Ft=1300N，使用MATLAB对运动过程受力进行仿真分析，得出管口对行走轮的支持力N1及摩擦力f1随角度φ变化的曲线，如图4所示。

图4 打磨机器人受力变化图Fig.4 Force change of grinding robot

由图4可看出，打磨机器人运行过程中，在其自身坐标系内，φ=0时，重力G在Y轴负向分力最大，X向分力为零，此时G与N1方向相反，N1需要与G和预夹紧力Ft的合力达到平衡，因此N1达到最大值1800N。随着φ的增大，G在Y轴负向的分力不断减小，X轴负向分力不断增大，φ=π/2时，G在Y轴正向分力为零，X轴负向分力达到最大，f1和f2方向均为X轴正向，f1和f2的合力与重力G达到平衡，因此此时f1达到峰值(非最大值)416.2N。φ=π时，G在Y轴正向分力达到最大，X向分力为零，此时G与N1方向相同，G和N1的合力与预夹紧力Ft平衡，因此N1达到最小值800N。φ=3π/2时，G在Y轴正向分力为零，X轴正向分力达到最大，此时f1和f2方向相反，f1需要与f2和G的合力进行平衡，因此f1达到最大值583.8N。最终随着φ增加至2π，N1和f1完成一次周期性变化，打磨机器人也完成了一个工作循环。

3 有限元仿真分析及现场样机试验

3.1 极限载荷下的有限元仿真分析

使用SOLIDWORKS软件建立插口端打磨机器人的虚拟样机模型(图5)。

图5 打磨机器人虚拟样机Fig.5 Grinding robot virtual prototype

首先，将SOLIDWORKS中建立的虚拟样机模型导入ANSYS Workbench，并对模型进行适当简化，省略钢丝绳、链条和皮带，可连接部件施加载荷，模拟省略的零部件。

然后，定义主体框架材质为结构钢，轴承座等零部件材质为球墨铸铁，行走轮材质为橡胶，并将电机、钢丝刷等部件定义为刚体，定义各个零件之间的接触，设定划分网格的各个参数后，自动划分网格。

根据之前对机器人运动过程的受力分析可知，在打磨机器人运行过程中，φ=0时，打磨机器人行走机构及夹持机构的主梁在Y向受力达到最大值；φ=3π/2时，其在X向受力达到最大值，因此对打磨机器人模型分别施加这两个极限工况下的载荷及约束，并得出分析结果。

图6所示为插口端打磨机器人在φ=0工况下的有限元分析结果，由图6a可看出，应力最大值129.44 MPa在夹持机构右侧后方轴承座与螺栓连接处，零部件材料为球墨铸铁，屈服强度为250 MPa，安全系数为1.9，满足力学要求。由图6b可看出，应变最大位置为夹持机构左侧后方轴承座与夹持支架接触位置，最大应变为7.263 2×10-4，满足刚度要求。

图7所示为插口端打磨机器人在φ=3π/2工况下的有限元分析结果，由图7a可看出，应力主要集中在压紧机构主梁与横梁交接处，最大应力为116.34 MPa，零部件材料为Q235钢，屈服强度为235 MPa，安全系数为2.0，满足力学要求。由图7b可看出，应变最大位置为夹持机构左侧前方轴承座与螺栓连接处，最大应变为6.077 8×10-4，满足刚度要求。

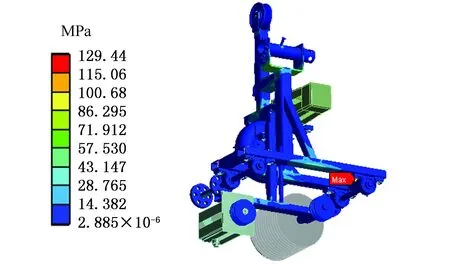
(a)应力云图

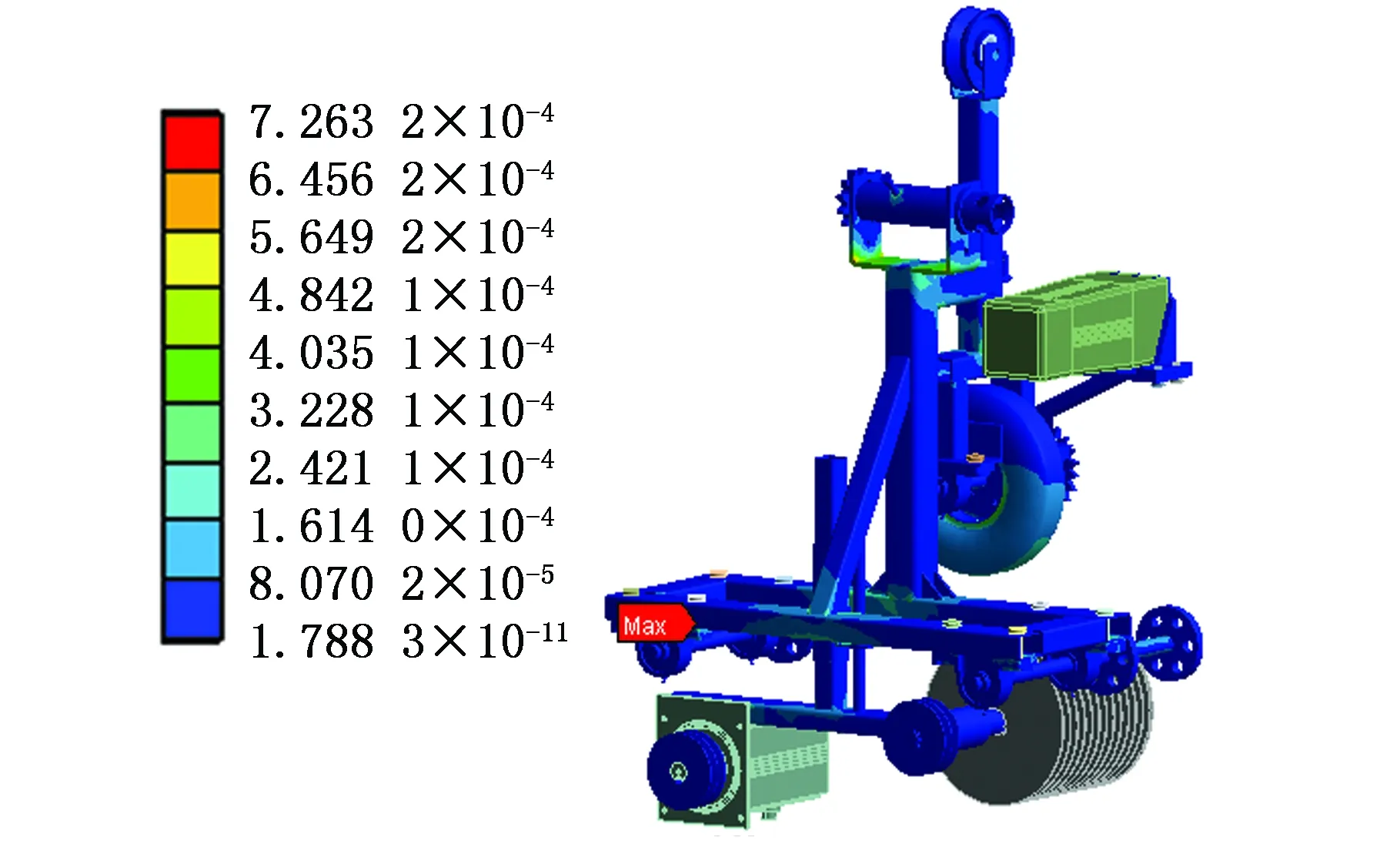
(b)应变云图图6 打磨机器人分析结果(φ=0)Fig.6 Analysis of grinding robot(φ=0)

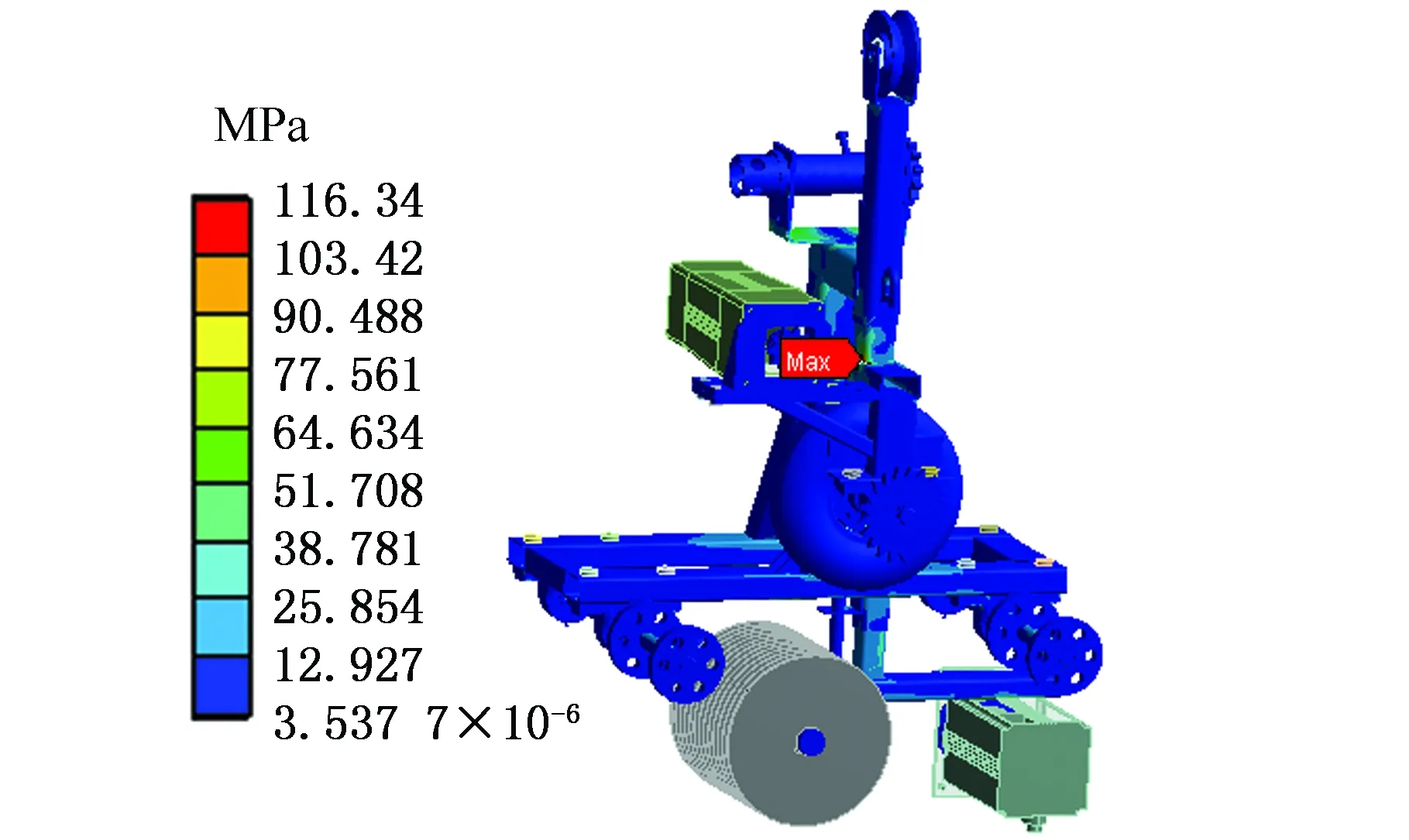
(a)应力云图

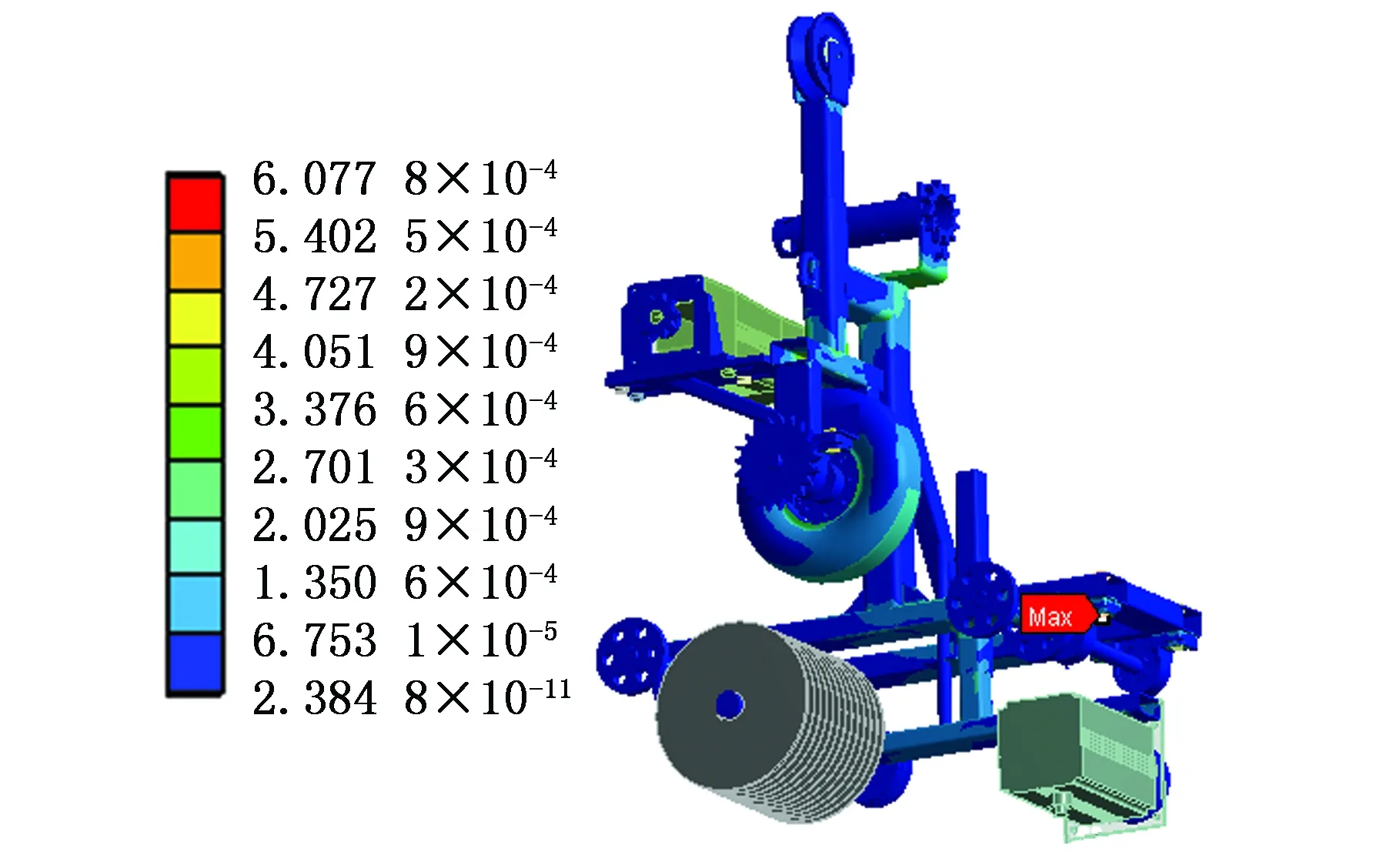
(b)应变云图图7 打磨机器人分析结果(φ=3π/2)Fig.7 Analysis of grinding robot (φ=3π/2)

3.2 有限元模态分析

打磨机器人的振动特性对其自身工作寿命及其打磨质量有重要影响。本文对其进行了前6阶模态的振型分析。由仿真结果可清楚地了解各阶振型的特征，前6阶的模态频率及振型特征如表2所示，相应的振型云图见图8。

表2 打磨机器人6阶模态频率及振型特征

图8 打磨机器人前6阶模态振型图Fig.8 The first sixorder modal shapes of grinding robot

由图8可知，打磨机器人1阶振型主要表现为行走机构主梁在OXY平面沿X轴的摆动，最大变形量为10.068 mm；2阶振型主要表现为行走机构主梁在OYZ平面沿Z轴的摆动，最大变形量为9.231 4 mm；3阶振型主要表现为夹持机构框架及末端执行机构横梁在OYZ平面沿Y轴的弯曲振动，最大变形量为5.899 4 mm；4阶振型表现为末端执行机构横梁绕Y轴的扭转摆动，最大变形量为9.144 2 mm；5阶振型表现为总体框架绕Z轴的扭转摆动，最大变形量为6.037 7 mm；6阶振型表现为末端执行机构总体绕X轴的扭转摆动，最大变形量为9.377 5 mm。通过对前6阶振型的分析可以看出，该打磨机器人的前6阶模态在行走机构主梁及末端执行机构横梁产生最大变形。

由表2可知打磨机器人前6阶固有频率的范围是25.032～42.090 Hz。为使打磨机器人在工作时不发生共振，机器人的固有频率与外部激励频率需满足如下关系[16]：

0.75ω0<ω<1.3ω0

式中，ω0为打磨机器人固有频率；ω为激励频率。

由于驱动电机转速较慢，外部激励主要为打磨伺服电机(其带动钢丝刷进行打磨工作时的转速为800～1 000 r/min)，因而产生的激励频率低于16.7 Hz，与打磨机器人前6阶频率25.032～42.090 Hz不在同一区间内，因而打磨机器人在工作过程中不会发生共振，说明此结构设计较为合理。

3.3 现场试验

以上述设计及计算为基础，制作了一台插口端打磨机器人样机，并在现场进行了试验测试，如图9所示。

图9 打磨机器人现场工作图Fig.9 Field running of grinding robot

现场样机试验中，预应力钢筒混凝土管道管口打磨机器人表现出以下优势：

(1)工作安全可靠。在工作过程中设备运行稳定，振动较小。

(2)打磨效率提高。拆卸及安装设备平均需5 min，完成一端打磨需4.5 min。设备工作过程中，可去完成另一台设备的拆卸与安装，打磨效率约是人工打磨效率的3倍。

(3)自动化程度高。打磨过程中无需人工在旁协助，可自行完成打磨。

(4)打磨质量良好。打磨面光滑，除锈效果好，打磨等级可达到St3级，而人工打磨一般达不到St2级，仅可去除表面砂浆等附着物(图10)。

(a)人工打磨 (b)打磨机器人打磨图10 打磨质量对比图Fig.10 Polishing quality comparison

4 结论

设计了一种自行走式混凝土管道管口打磨机器人，对其进行了受力分析，针对其滑移情况建立了预夹紧力模型，创建了虚拟样机，运用ANSYS Workbench软件对其进行了有限元分析，并制作了打磨机器人样机进行现场打磨试验。仿真及试验结果表明，该打磨机器人可靠性高，运行稳定，打磨质量高，具有自动打磨混凝土管道管口的功能，提高了管口打磨的效率。