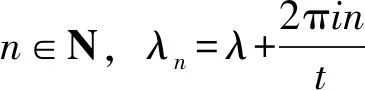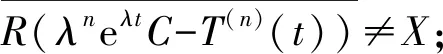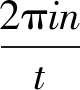C-半群高阶微分算子的谱

刘 瑞， 王小霞

(延安大学 数学与计算机科学学院， 陕西 延安 716000)

在经典算子半群理论中， 谱映射定理是非常重要的组成部分， 许多数学工作者对此进行了广泛的研究， 文献 [1-6]研究了C0-半群、C-半群和积分C-半群T(t)的谱， 文献[7-8]研究了双参数C0-半群和双参数C-半群谱， 本文在C-半群的基础上， 结合文献[9]讨论了C-半群T(t)的高阶微分算子T(n)(t)的谱以及T(n)(t)的谱和T(t)无穷小生成元A的谱之间的关系.

定义1[10]设X为Banach空间，B(X)是X中有界线性算子全体，C∈B(X)是单射，B(X)中的算子族{T(t)∶t≥0}称为C-半群， 如果满足：

1)T(0)=C;CT(t+s)=T(t)T(s);

其生成元A定义为

定义2[3]设{T(t)∶t≥0}是复Banach空间X上C-的半群， 称集合

}λ∈C∶(λC-T(t))-1∈B(x),t≥0}

为C-半群{T(t)∶t≥0}的预解集， 记为ρ(T(t))；称集合Cρ(T(t))为C-半群{T(t)∶t≥0}的谱， 记为σ(T(t)).

定义3[11]设{T(t)∶t≥0}是X上C-的半群， 若存在t0>0使得对每个x∈X，T(t)x关于t>t0在X上可微， 则称{T(t)∶t≥0}是t>t0的可微C-半群；若T(t)x关于t>0在X上可微， 则称{T(t)∶t≥0}是可微C-半群.

引理1[12]设{T(t)∶t≥0}是由A生成的C-半群， 则T(t)x∈D(A)且

x∈D(A),t≥0.

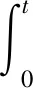
1) (λI-A)Bλ(t)x=eλtCx-T(t)，x∈X；

2)Bλ(t)(λI-A)x=eλtCx-T(t)x，x∈D(A).

定理1 设{T(t)∶t≥0}是由A生成的t>nt0的可微C-半群， 若λ∈σ(A)， 则λneλt∈σ(T(n)(t))， 即λnetσ(A)⊂σ(T(n)(t)).

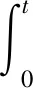
AT(t)x+λT(t)x+λ2Bλ(t)x,

…

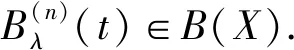
由引理2有(λI-A)Bλ(t)x=eλtCx-T(t)x， 两端同时关于t求n次导数可得

即

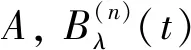
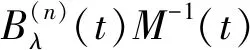
定义4[3]设{T(t)∶t≥0}是复Banach空间X上的C-半群， 对{T(t)∶t≥0}的谱σ(T(t))进行如下分类：

若(λC-T(t))-1不存在， 则称λ为C-半群 {T(t)∶t≥0} 的点谱， 记为σp(T(t))；

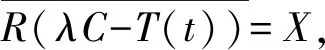
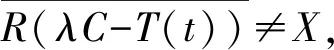
由定义4， 谱分为三个互不相交的部分， 即点谱、连续谱和剩余谱.下面将讨论对于可微C-半群{T(t)∶t≥0}， 它的高阶微分算子T(n)(t)的谱各个部分与T(t)的生成元A的谱相应部分之间的关系， 首先考虑点谱.

定理2 设{T(t)∶t≥0}是由A生成的t>nt0的可微C-半群， 则

λnetσp(A)⊂σp(T(n)(t))=λnetσp(A)∪{0}.

更明确的就是：

1) 如果λ∈σp(A)， 则λneλt∈σp(T(n)(t))；

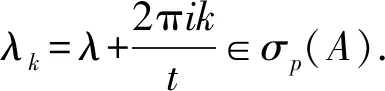
证明1)如果λ∈σp(A)， 则存在x0∈D(A)且x0≠0使得

(λI-A)x0=0,

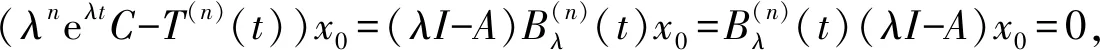
2) 如果λneλt∈σp(T(n)(t))， 则存在x0∈D(A) 且x0≠0使得

(λneλtC-T(n)(t))x0=0.

a) 若λ=0， 则显然λneλt=0；

b) 若λ≠0， 令f(s)=λ-ne-λsT(n)(s)， 作为s的函数它不恒为零， 将f(s)以t为周期进行奇式或偶式延拓， 其Fourier系数必有一个不为零， 从而存在k∈N使得

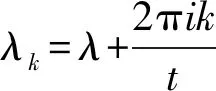
令‖T(t)‖≤Meωt， 则当Reμ>ω时， 由引理3有

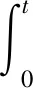
又

因为A是闭的， 有xk∈D(A)且(λkI-A)xk=0， 所以，λk∈σp(A).

下面对连续谱和剩余谱进行研究.

引理4[15]设Y是赋范线性空间X的真闭子空间， 又设x0∈XY为任意， 则存在x*∈X′且x*≠0使得对一切y∈Y， 有〈x*,y〉=0.