引入视觉注意机制的区域立体匹配方法*

杜棋东

（广州铁路职业技术学院教育技术中心，广州510430）

1 引 言

立体匹配是虚拟现实、机器人视觉等领域的一项重要研究内容，能够通过多视点图像计算出物体的深度信息，对视觉导航、障碍物检测等实际应用有着重要的作用[1-2]。根据不同匹配的基元，立体匹配分为特征点匹配和区域立体匹配[3]。其中，区域立体匹配是以一个区域为匹配基元，通过匹配其他图像中最优匹配区域获取最终视差图的过程。常见的方法包括归一化灰度互相关NCC 算法（Normalized Cross Correlation）、绝对误差和SAD 算法（Sum of Absolute Differences）、误差平方和SSD 算法（Sum of Squared Differences）。此类常见立体匹配方法往往只关注图像表面上的像素数据[4]，缺乏人眼的感知关注，所以往往会影响算法效率甚至发生视差图错配。

故此提出一种基于视觉注意机制的方法。此方法能够模拟人眼快速感知外界抽象物体，快速计算其显著性目标区域，减少搜索空间，并降低识别的计算复杂度，在文献[5－7]研究工作的基础上，引入视觉注意计算模型（Itti 模型），提取图像亮度、颜色、方向等非空间特征，然后将彩色图像分割若干区域，建立图像间立体匹配关系，接着计算两幅图的视差值，通过视差值提取并优化视差图，获取最终的视差图。

2 设计方法

视觉注意机制是基于生物学的心理调节机制，能够有选择性地指向环境中的某一个焦点而忽略其他事物的认知过程，其感知具备选择能力。引入视觉注意机制的Itti 模型，首先基于双目视觉，通过中央-周边（Center-Sound）算子计算输入图像的颜色特征、亮度特征、方向特征，获得多特征、多尺度的量度结果并合成左右两幅显著图，反差大的区域代表视觉注意力高的区域，根据不同显著图的值计算显著区范围，然后采用颜色分割方法将图像划分为若干区域。在计算各区域颜色和灰度相似性的基础上，建立图像间的匹配关系，根据左右两幅图匹配计算，得出各个像素点的视差值，再由视差值生成视差图，最后采用平面相似性估计方法[8]合并场内的近似属于同一视差的平面，得到新的视差图，即为深度特征图。引入视觉注意机制的区域立体匹配方法流程如图1 所示。

3 具体计算

3.1 非空间特征计算

非空间特征提取反映了由视觉感知到初级视觉特征信息的处理过程，通过对亮度、颜色和方向等非空间特征的提取，得到各类特征在不同尺度下的多特征图。

关于亮度特征提取，首先根据下式将彩色图转化为灰度I：

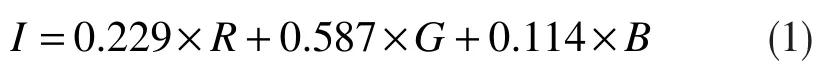
再计算灰度I 在s 尺度下的亮度特征图。若输入图像是灰度图，则直接获取亮度信息即可。

关于颜色特征提取，根据下式计算RG 和BY 的色差：

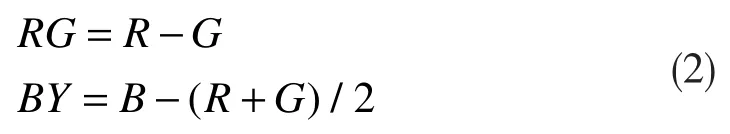
然后再计算各个领域的色差均值，其中Y=(r+g)/2+(r-g)/2-b, R=r-(g+b)/2,G=g-(r+b)/2,B=b-(r+g)/2，最后得到s 尺度下的颜色特征图RG、BY。

关于方向特征提取，Gabor 在这方面具有良好的方向选择和尺度选择特性，因此采用Gabor 滤波器方法，根据下式对s 尺度下的灰度图像I 进行滤波：

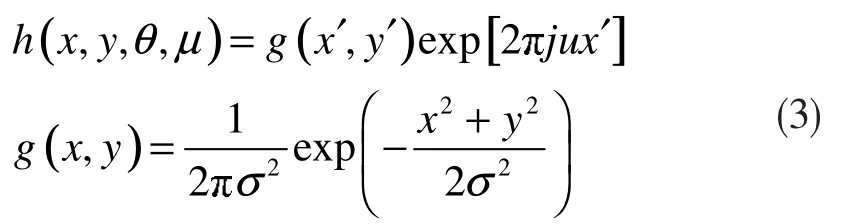
其中，x′=xcosθ+ysinθ，y′=-xsinθ+ycosθ，θ 为主频方向，μ 为频率，θ∈{0°, 45°, 90°, 135°}，进而可得到方向特征图O(θ)。

3.2 深度信息计算

深度信息计算对视觉加工处理至关重要，是进行物体识别的重要步骤，下面通过彩色图像区域分割、立体匹配、视差图提取以及视差平面优化等步骤，计算深度信息。

3.2.1 图像分割和SAD 立体匹配

彩色图像区域分割的实质就是从复杂的背景粗化提取整体信息，把具有相似性质的像素连通成特定区域。各种场景的物体姿态特征提取，其立体视差变化主要体现在颜色区域的轮廓边界上，这种情况下采用均值偏移（Mean shift）算法[9]，此算法的实质是核密度估计，算法核心是对特征空间中的样本点进行聚类，得到密度梯度为零的模式点。彩色图像分割首先借助Mean shift 算法将图像中的像素进行聚类，找到不同色彩的聚类点，然后进行二值化处理，使图像中的灰度级较处理前有所减少。

在上述区域分割的基础上，计算最小的SAD 差异区域，即匹配区域。SAD 的基本思想是差的绝对值之和，即通过各个像素值之差的绝对值求和，以此来评估区域的相似度。

SAD 计算如下式：

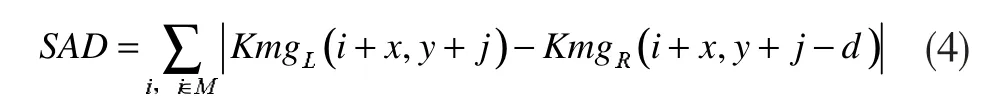
其中：M 为n×n 大小的窗口，类似于卷积核；d为视差范围；KmgL(i,j)表示以(i,j)为中心的基准图待匹配像素的所有灰度值的均值，KmgR(i,j)表示以(i,j)为中心的配准图的匹配点的所有灰度值均值。

对M 窗口中的全部代价函数进行加权聚合，通过以下聚合函数式可计算匹配点与候选点之间的聚合值：

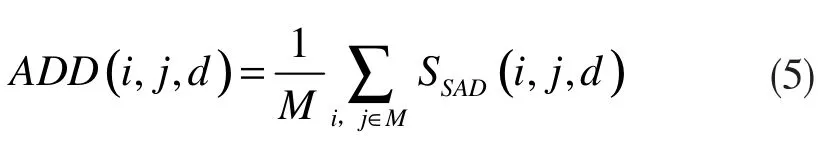
对视差值d 的计算如下式：

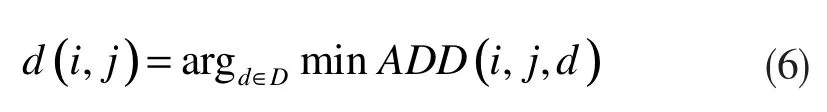
其中D 表示视差范围。

3.2.2 视差图优化

关于视差层提取，所采用的是平面相似性估计方法[10]，即下式：

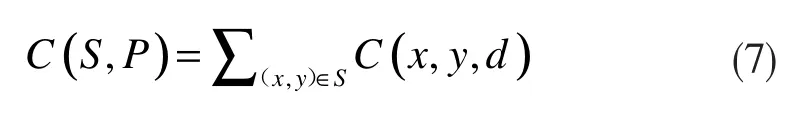
其中，S 为分割区域，P 为视差平面，C 为匹配代价函数，通过C 来判断S 是否属于P，并将同样视差值的平面划分为一类，合并相似区域，合并之后的视差图即为最终视差图。此处，其中、均是P 的参数。

为解决视差图错误匹配产生噪声的问题，利用显著性检测法对视差图进行优化。首先对初步视差图利用基于频域的HFFT 方法[11]检测显著图，再对其进行非空间特征计算；接着判断显著图的显著度值是否比设定的阈值大，如果小于阈值，则判断为图像正常边缘，如果大于阈值，采用多点均值滤波进行处理，即对窗口范围内的所有显著点进行处理。其中，中心点值用去除最小值点与最大值点后的均值代替；最后重复1~3 次流程进行视差图优化。其具体流程如图2 所示。

图2 优化视差图流程

4 实验分析

实验使用的计算机配置为：Intel Core i3 8100 3.6GHz，Windows 64 位操作系统；程序在MATLAB 2013b 中实现，实验图采用Teddy 标准双目视图；标准数据实验采用NCC 算法、SSD 算法、SAD 算法和提出的算法进行实验比较。为了方便实验，只使用Teddy 的右图像。实验效果如图3 所示。其中图3(a)~(d) 分别表示NCC、SSD、SAD 与提出方法的匹配代价计算结果。图3(e)与图3(f)用于表示标准视差与原始图匹配效果的好坏对比。

图3 各算法实验效果对比

从图3(d)和图3(a)可知，新方法虽然在展示画布的纹理信息上不够细致，但对物体边缘的处理还是优于NCC 算法的。从图3(d)和图3(b)可知，新方法能较好地处理区域物体深度信息。从图3(d)和图3(c)对比可看出，新方法相对于SAD 算法，不仅能较好解决遮挡区域的视差问题，而且视差精度较高，示例图像中的布偶和玩具房轮廓边缘效果明显，可信度高。与其他3 种算法的误差率对比如表1 所示，运算时间上的对比则如表2。

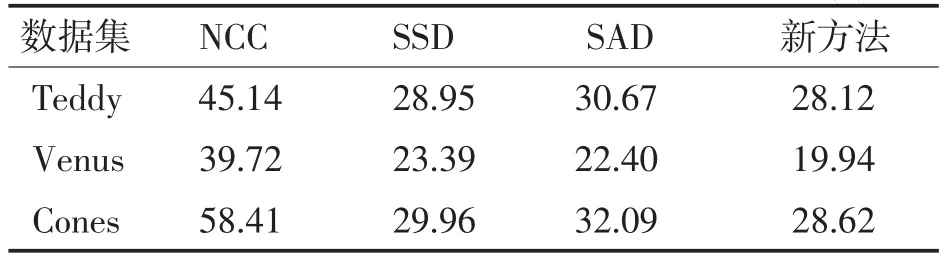
表1 其他算法与新方法误差率对比 单位：%

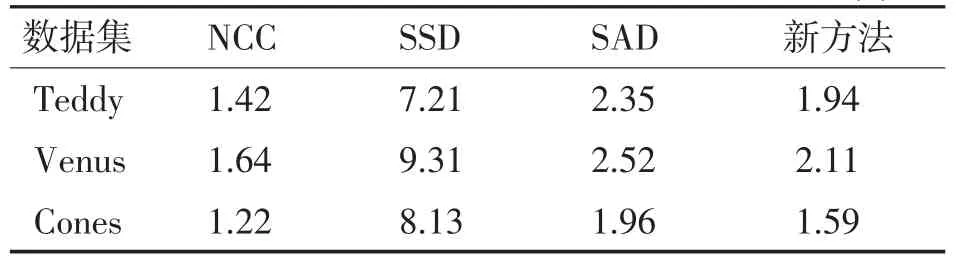
表2 其他算法与新方法运算时间对比 单位：s

在表2 中可以看出，NCC 算法的运算速度最快，与新方法对比快了20%左右，但其匹配误差率也高于新算法2 倍多。SAD 算法与SSD 对比，在误差率相差不大的情况下，运算时间较快，故而SAD算法优于SSD 算法。新方法与SAD 对比，误差率低于SAD 算法，运算速度也略高于SAD 算法，能够满足图像立体匹配场景下的应用要求。

5 结束语

针对算法效率的提升与降低出错率，提出了一种引入视觉注意机制的区域立体匹配算法。在保证图像一定精度的情况下提高匹配速度和效率，保证匹配的准确性。实验表明，所述方法相比于精度较高、速度较快的SAD 算法，能够提高15%速度，同时精度提高3%，为立体匹配技术在视觉导航、障碍物检测等方面的应用奠定了良好基础。