四足机器人单腿跳跃柔顺性的规划和控制研究
陈建文,谭跃刚,雷成林,陶红武
(武汉理工大学 机电工程学院,湖北 武汉 430070)
四足机器人以自然界的四足动物为仿生对象。四足机器人只需一些离散的落足点,就可以在各种复杂路面上完成行走,跨越障碍,有非常好的地形适应能力,在工程探险,抢险救灾,军事侦察,物资运输等方面具有广泛的应用前景[1]。
跳跃步态是四足生物的典型运动步态之一,四足生物可以通过跳跃轻松越过障碍物和快速移动。国内外许多学者都对四足机器人跳跃展开了研究,1986年Raibert[2]最早对单腿弹跳机器人进行研究,制作了单腿跳跃样机,其单腿样机能独立保持平衡并周期性稳定跳跃。Sato等[3]仿照猫腿部的生理特点制作了双足样机Sugoi-Neco legs,在跳跃过程中样机足底加入障碍物也能实现稳定跳跃,有较好地地形适应性。MIT的Cheetah 2代四足机器人[4]采用阻抗控制的方法来控制腿部运动,能以跳跃步态轻松跨越障碍物,动态性能很好。国内的孟健[5]、钟建锋[6]、高炳微[7]和张雪峰[8]等对基于单腿样机对四足机器人单腿跳跃的控制方法和轨迹规划进行了研究,取得了一定的研究成果。此外,还有学者从蝗虫[9],袋鼠[10]等生物汲取灵感对机器人的跳跃运动进行了分析和研究。
国内外的研究者在机器人跳跃运动的运动机理,轨迹规划和运动控制上均取得了较好的研究成果,但是在机器人跳跃过程中依然存在足端冲击力大、柔顺性不好的问题。在跳跃过程中,机器人足端与地面的接触时间短,能量输出大,机器人在起跳和着地时足端存在很大的冲击力。一方面冲击力会破坏机器人机械结构,影响控制系统和传感系统的可靠性,另一方面冲击力会影响机器人行走的平衡性能,严重时甚至会发生倾倒。解决机器人跳跃过程的柔顺性问题,能有效地改善机器人足端受力情况,提高机器人的动态运动稳定性,实现高性能的跳跃运动。
针对单腿跳跃的柔顺性问题,笔者以四足机器人单腿系统为研究对象,建立单腿系统的运动学模型,分析单腿跳跃运动并规划了足端的运动。设计了一种基于阻抗控制的单腿控制系统,并对单腿的竖直跳跃运动进行仿真,为后续研究提供设计和控制依据。
1 运动学模型
1.1 机械结构
单腿结构设计是以生物狗为依据,根据生物狗后腿各肢段尺寸和比例进行设计。图1为四足机器人单腿,它为三段式结构,具有两个自由度,有利于简化运动控制,提高运动性能。腿部肢段采用平行四边形机构,利用平行四边形特性,将髋关节和膝关节的电机置于机身,从而减小腿部运动惯量,提高腿部的灵活性。其结构原理如图2所示,杆件l1和杆件l4为原动杆件,其余杆件为从动杆件,各杆长参数如表1所示。

图1 四足机器人单腿

图2 单腿结构原理图 图3 单腿结构简图

表1 单腿杆长参数
1.2 运动学分析
根据平行四边形机构的运动学特点,将平行四边形机构进行运动等效简化,去除平行四边形的两个平行杆,得到单腿结构简图,如图3所示。在单腿系统中,驱动元件为电机。θ1,θ2分别为电机角位移,φ1,φ2,φ3分别为杆件间的夹角,两者的关系如式(1)所示,且根据右手定则可知,θ1和θ2均为负值。
φ1=360°+θ1
φ2=θ3=θ2-θ1
φ3=360°-φ2=360°+θ1-θ2
(1)
根据杆长和关节角度,用D-H(Denavit -Hartenberg)法对单腿运动学进行分析,列出D-H参数表,如表2所示。

表2 单腿D-H参数表
根据D-H参数求连杆变换矩阵,其中01T表示坐标系{1}相对于坐标系{0}的坐标变换,12T表示坐标系{2}相对于坐标系{1}的坐标变换,依此类推。s1表示sinθ1,c1表示cosθ1,s12表示sin(θ1+θ2),c12表示cos(θ1+θ2),s123表示sin(θ1+θ2+θ3),c123表示cos(θ1+θ2+θ3)。
01T=c1-s100
s1c100
0010
000112T=c2-s20l1
s2c200
0010
0001
23T=c3-s30l2
s3c300
0010
000134T=100l5
0100
0010
0001
04T=c123-s1230l2c12+l1c1+l5c123
s123c1230l2s12+l1s1+l5s123
0010
0001
(2)
由变换04T可知,足端坐标(x,y)可表示为:
x=l2cos(φ1+φ2)+
l1cosφ1+l5cos(φ1+φ2+φ3)
y=l2sin(φ1+φ2)+
l1sinφ1+l5sin(φ1+φ2+φ3)
(3)
根据式(3)和φ1,φ2,φ3的取值范围,计算足端可达工作空间,如图4所示。

图4 足端可达工作空间
由式(1)中φ1,φ2,φ3和θ1,θ2的关系,可将足端位置和电机角位移关联起来:
x=l2cosθ2+(l1+l5)cosθ1
y=l2sinθ2+(l1+l5)sinθ1
(4)
求运动学逆解得:
θ1=arcsinx2+y2+(l1+l5)2-l222l1x2+y2-arctanxy
θ2=-arcsinx2+y2-(l1+l5)2+l222l2x2+y2
(5)
为了进一步得到足端运动速度和电机转动速度之间的关系,将式(4)两边对时间求导,得到单腿的速度雅可比矩阵。
x·
y·=-(l1+l5)sinθ1-l2sinθ2
(l1+l5)cosθ1l2cosθ2θ1·
θ2·
(6)
速度雅可比矩阵J为:
J=-(l1+l5)sinθ1-l2sinθ2
(l1+l5)cosθ1l2cosθ2
(7)
2 跳跃运动分析与轨迹规划
2.1 竖直跳跃运动分析
为了对单腿的跳跃运动进行规划,首先需要对单腿的跳跃运动进行分析。单腿的跳跃可按照足端是否触地分为腾空相和着地相,腾空相又可根据腾空最高点分上升阶段和下落阶段,着地相可根据着地最低点分为缓冲阶段和起跳阶段。图5为单腿跳跃运动的各个阶段。
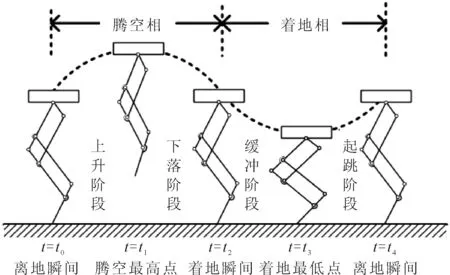
图5 跳跃运动各阶段
在四足机器人中,腿部主要功能是支撑躯体并带动躯体运动,虽然腿部连杆具有一定质量,但机器人的大部分质量集中在躯体部分。为便于研究单腿运动,对单腿系统进行简化分析,忽略腿部连杆的质量。根据腿部关节的刚度和阻尼,将单腿视为“质量-弹簧-阻尼”系统,如图6所示。其中,m为系统质量,k为系统刚度,c为系统阻尼,H为单腿初始长度,Fτ为驱动器提供的力。

图6 “质量-弹簧-阻尼”系统
腾空相时,忽略空气阻力单腿只受重力作用,腾空相动力学方程为:
x··=0
y··=-g
(8)
着地相时,单腿受重力和地面的反作用力。在着地瞬间,单腿系统速度最大,具有最大动能,地面对单腿有较大的冲击力。随后进入缓冲阶段,单腿系统消耗并存储一部分动能,直至速度降为零,到达着地最低点,此时动能为零。接着进入起跳阶段,腿部驱动器提供力矩和能量,驱使单腿蹬地并起跳。
缓冲阶段动力学方程:
x··=0
my··=-mg+k(H-y)+cy·
(9)
起跳阶段动力学方程:
x··=0
my··=-mg+k(H-y)-cy·+Fτ
(10)
2.2 足端轨迹规划
根据单腿系统竖直跳跃各阶段运动分析,规划足端的运动轨迹。以单腿髋关节为原点建立竖直平面坐标系,在此坐标系对足端运动进行规划。在竖直跳跃过程中,为保证足端落地点不变,足端横坐标保持不变:
x=0
(11)
足端纵坐标根据不同运动阶段切换运动轨迹:
y=
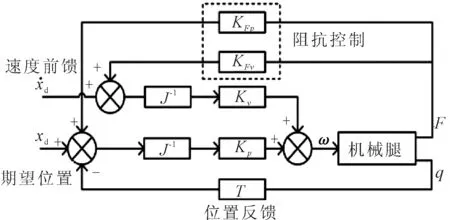
-D(t0≤t -D+vc(t-t2)+12as(t-t2)2(t2≤t -D+S(t=t3)着地最低点 -D+S+12ac(t-t2)2(t3 (12) 式中:D为足端着地点与髋关节的垂直距离;vc为着地时单腿相对地面的速度;as为缓冲加速度;S为缓冲距离且S=v2c/2as;ac为起跳加速度。 腾空相时为维持运动的稳定以及修正起跳误差,保持足端竖直位置为D。 缓冲阶段时根据冲量定理F×t=m×Δv,为减小冲量作用,减小冲击力,规划足端相对的地面速度为零,在运动规划坐标系下,接触地面时足端速度大小为vc。为保持接触力平稳,机身以匀减速到达最低点,在运动规划坐标系下,足端为匀减速运动,加速度为as。 起跳阶段时为保持足端接触力平稳无冲击,机身以匀加速起跳,直到足端离地,在运动规划坐标系下,足端为匀加速运动,加速度为ac。 在单腿的跳跃运动中,因跳跃运动具有动态性高和瞬间功率大的特点,在单腿着地和起跳时存在较大的冲击力。这对单腿的控制系统提出了更高的要求:①控制系统要有较高的快速性,要在触地的极短时间内对系统进行有效控制;②控制系统需对足端冲击力进行控制,通过控制有效减小足端冲击力。 基于阻抗控制的思想,设计了一种单腿控制系统,带速度前馈的位置控制器为内环,力反馈型阻抗控制器为外环。为提高单腿系统响应的快速性,采用速度前馈控制的方式缩短响应时间。为了减小足端接触力冲击,采用力反馈型阻抗控制器实现力的柔顺。其控制框图如图7所示。 图7 单腿控制系统框图 其中,xd为期望位置;x·d为期望速度;F为足端与地面的接触力;T为单腿前向运动学方程;J-1为单腿速度雅可比矩阵的逆;Kp为位置控制系数矩阵;Kv为速度控制系数矩阵;KFp为阻抗刚度系数矩阵,其值为系统期望刚度的倒数;KFv为阻抗阻尼系数矩阵,其值为系统期望阻尼的倒数;Kp、Kv、KFV、KRp均为对角矩阵;q为关节角度。 仅对足端进行位置控制时,电机的输入转速ω由位置反馈控制部分和速度前馈控制部分共同决定: ω=KpJ-1[xd-T(q)]+KvJ-1x·d (13) 机器人足端受到外力或外力矩时会产生较大的冲击力。为实现力的柔顺,将力反馈引入位置反馈控制和速度前馈控制中,通过改变力反馈系数KFp和KFv,调整整个系统的阻抗,引入力反馈后: ω=KpJ-1[xd-T(q)+KFpF]+ KvJ-1(x·d+KFvF) (14) 根据式(14)可知,系统受外力时允许出现一定的位置偏差和速度偏差,降低了足端位置控制刚度,增加了足端速度的粘滞阻尼,改变了系统的阻抗,从而使足端表现出一定的柔顺性。KFp越大,末端刚度越低;KFv越大,末端的粘滞阻尼越小。此外,为避免系统不稳定,Kp取值不宜过大。 为了验证足端轨迹规划和阻抗控制方法的有效性,对四足机器人单腿系统进行了Adams-Simulink联合仿真。将单腿三维模型导入Adams中,并相应地定义单腿各运动副,在模型中约束单腿平台的3个旋转自由度,从而保证单腿在垂直面运动而不发生侧向倾倒,单腿系统的Adams模型如图8所示。 图8 单腿系统Adams模型 根据单腿控制系统框图,在Simulink中建立控制模型,并将Simulink控制模型与Adams模型进行联合仿真。通过参数整定,选取控制参数如表3所示。 表3 控制参数表 为了验证阻抗控制对足端接触冲击力的柔顺作用,在仿真环境下将单腿系统从高处自由下落。通过两组实验对比分析,一组为无阻抗控制自由下落,锁定关节位置,另一组为有阻抗控制自由下落。在自由下落仿真中,足端距地面高度h=0.073 m。仿真结果如表4和图9所示。 表4 自由下落过程中接触力对比 图9 自由下落力响应和位置响应对比 在足端接触地面之前,单腿的运动为自由落体运动。足端接触地面瞬间,足端与地面会产生瞬间冲击力峰值,随后接触冲击力在一小段时间内保持稳定,随着单腿逐渐趋于静止,接触力逐渐减小最后等于重力。在无阻抗控制的自由下落中,冲击力的瞬间峰值(1 141 N)与冲击力稳定值(1 050 N)相差不大,随后足端在冲击力的作用下回弹一定高度并再次下落,造成二次冲击(246 N)。但在带阻抗控制的自由下落中,冲击力达到瞬时峰值(1 059 N)后,阻抗控制开始作用,足端回缩,其冲击力稳定值(723 N)有一定的减小,且由于足端的主动回缩,单腿不会回弹,消除了足端的二次冲击作用。根据仿真结果可知,基于阻抗控制的单腿控制系统有效地减小了接触力冲击,消除了二次落地的接触冲击,具有较好的柔顺效果。 根据式(12)的足端轨迹规划方程,在竖直跳跃运动仿真中,D=0.31,足端距地面高度为h=0.073 m,足端与地面接触速度vc=2gh=1.196 m/s。为限制缓冲距离,取缓冲加速度as=7.5 m/s2,为保证起跳高度相同,经参数整定,取起跳加速度ac=11.3 m/s2。将以上参数代入式(12)中,得到足端运动轨迹规划。以该足端轨迹作为期望输入,对单腿系统的竖直跳跃运动进行仿真。单腿系统的足端接触力、足端位置和足端离地高度如图10所示。 图10 竖直跳跃运动仿真 在竖直跳跃过程中,着地瞬间冲击力峰值为432 N,由于阻抗控制作用,着地过程中冲击力降至235 N。随着单腿的缓冲收缩接触力减小并稳定在75 N。缓冲阶段结束后单腿进入起跳阶段,起跳过程中,足端接触力稳定在90 N且平稳无冲击。随后进入下一次跳跃周期。跳跃过程中,足端位置幅值误差和相位误差均很小,跟踪效果较理想。且单腿多次跳起高度保持在0.073 m,跳跃运动具有较好的稳定性。 对比图9和图10的仿真结果,与自由下落仿真相比,在竖直跳跃仿真中,着地瞬间冲击力峰值(432 N)和着地过程冲击力稳定值(235 N)都比较小,柔顺性更好。造成这种差别的原因是在自由下落仿真中,足端仅在阻抗作用下回缩,而在竖直跳跃仿真中,不但有阻抗作用,跳跃过程中的缓冲运动也使接触冲击力减小了。在足端轨迹规划中,规划了单腿的缓冲阶段,缓冲阶段中足端与地面相对速度较小,减小了冲量作用,有效地缓冲了一部分冲击力。 根据仿真结果及以上分析可知,在竖直跳跃仿真中,在阻抗控制和足端轨迹规划的作用下,单腿系统和地面的接触冲击力小,具有较好的柔顺性,且足端位置跟踪效果理想,跳跃高度稳定。 以四足机器人单腿系统为研究对象,研究单腿跳跃运动时的柔顺性问题,通过对单腿的运动学模型和跳跃运动进行分析,规划了足端的运动轨迹。设计了一种基于阻抗控制的单腿控制系统,并在Adams-Simulink联合仿真环境下对单腿的跳跃运动进行仿真。仿真结果表明,四足机器人单腿系统在跳跃运动中具有较好的柔顺性。3 单腿控制系统
4 仿真分析


4.1 自由下落仿真对比

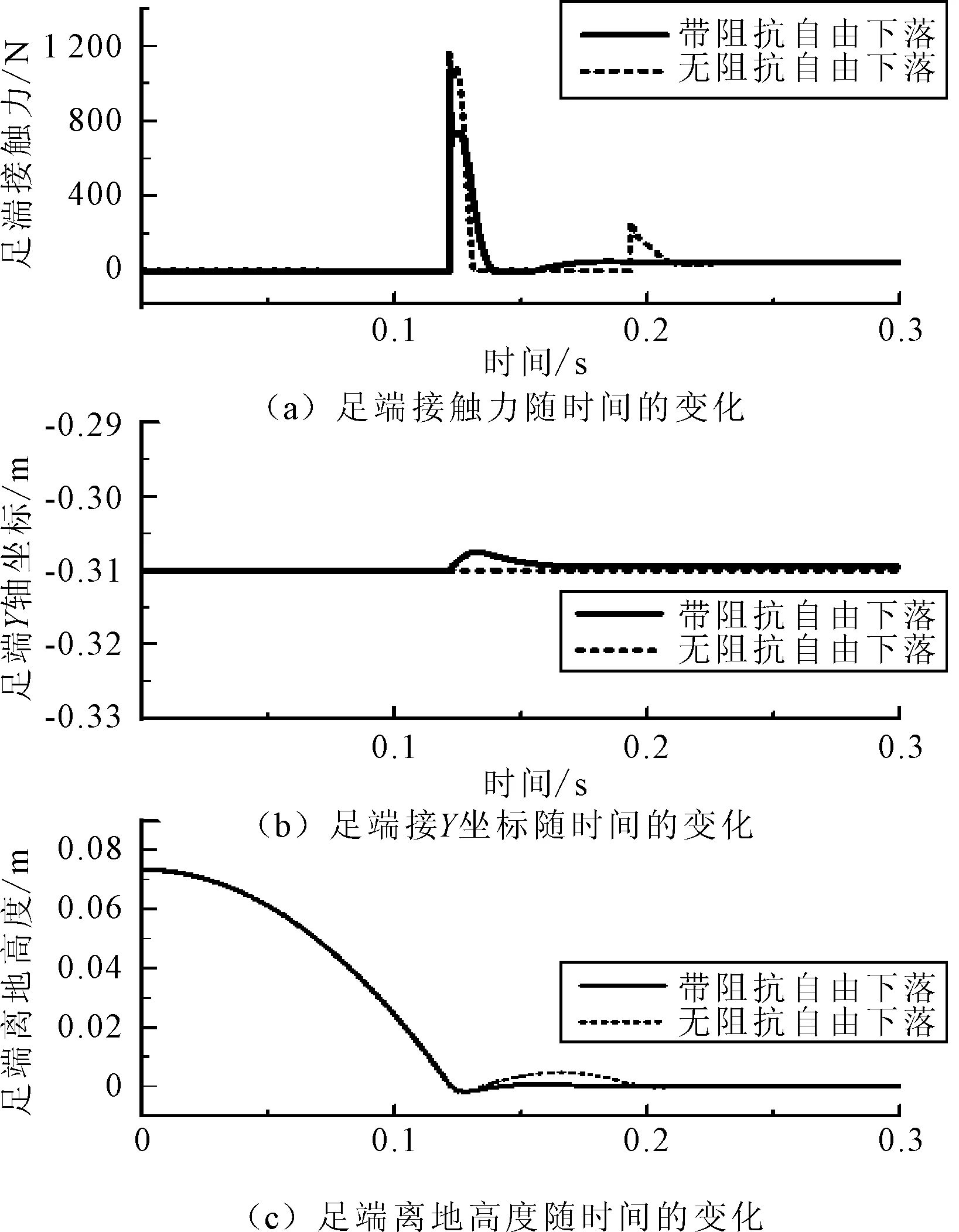
4.2 竖直跳跃仿真

5 结论

