基于动态检测的大齿轮精准插齿方法
刘福聪,王 鹏
(天津职业技术师范大学机械工程学院,天津 300222)
大型齿轮是大重型装备、大型精密设备的关键传动零件,插齿是加工大型圆柱内齿轮的重要工艺方法。当前对卫星定位精度需求越来越高,精准的卫星定位精度需求要求卫星定位设备中的精密大型内齿轮的齿距累积公差Fp达到国标4级以上。用于铣内齿的铣齿机精度较低,如果把铣头换为磨头,只能提高表面粗糙度,并不能提高分度精度。受直径规格限制,目前尚未开发出能够加工该类齿轮的精密磨齿机,加工精度只能依靠插齿加工方法保证。常规插齿加工精度可以达到国标6级,显然无法满足该类齿轮的加工要求。因此,研究大型齿轮的高精度插削方法和技术十分必要。
受机床零部件加工和装配精度、机床控制精度、机床稳定性等多方面因素的影响,研发更高精度的插齿机存在较大困难。在现有基础上,开发基于动态检测和靶向修正的大齿轮精准插齿加工方法,挖掘大型插齿机的加工潜力,进一步提高加工精度,已成为精密大型齿轮加工领域的一个重要研究方向。国内外专家学者和机床制造企业在齿轮在线测量方面做了大量工作,但仅限于对成品齿轮加工精度进行检测;在普通金属切削加工在线测量与误差实时补偿技术方面也做了大量工作,但缺少对齿轮加工过程进行实时检测和靶向修正的深入研究[1-4]。随着激光位移扫描技术和伺服控制技术的发展,插齿加工过程的实时检测和靶向修正具备了必要的技术条件。基于此,本文提出一种大型齿轮精准插齿加工方法。在插齿加工过程中,用激光位移传感器对切削过程表面进行扫描,建立切削状态数学模型,与理论状态的齿轮加工过程数学模型进行比较,并计算加工误差,通过控制系统对误差进行靶向修正。
1 插齿加工物理模型和数学模型
1.1 数控插齿机物理模型
本文以作者主持研发的重大专项项目“高档数控机床与基础制造装备”——YKW51250数控插齿机为研究对象。YKW51250数控插齿机是一台六轴高效精密数控插齿机,6个控制轴分别为:工作台旋转轴(C轴)、刀架旋转轴(C2轴)、主驱动轴(Z轴)、径向进给轴(X轴)、斜向让刀轴(Y轴)、让刀轴(X2轴)。其中C轴、C2轴、X轴3个轴的定位精度影响切齿精度[5]。合理简化插齿机、插齿刀和工件的结构,建立如图1所示的插齿加工“机床-插齿刀-工件”工艺系统的物理模型。
C轴、C2轴、X轴采用全闭环反馈控制,闭环反馈位置距离切削位置距离较远,且闭环反馈位置与切削位置之间存在较多弹性环节,弹性环节影响切削精度,所以需要进一步研究机床传动和切削原理,找到优化切削精度的方法,以提高机床切削精度。
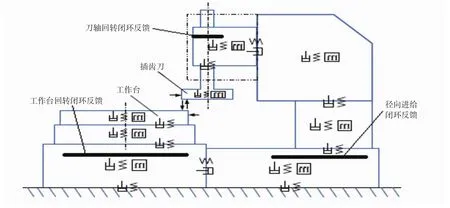
图1 YKW51250数控插齿机“机床-插齿刀-工件”工艺系统物理模型
某卫星定位设备需要的齿轮零件分度圆直径约为4 000 mm,齿形角为20°,变位系数为0。齿距累积公差Fp对卫星定位精度影响最大,要求其精度等级不低于国标4级,从《机械设计手册》可知齿距累积公差Fp≤54 μm。YKW51250数控插齿机工作台采用全闭环控制,在φ1 410 mm圆周位置,定位精度可达弧长±3 μm;放大到工件齿轮分度圆直径φ4 000 mm时,定位精度为弧长±8.25 μm。定位精度数值小于工件齿距累积公差要求的数值,且工件与C轴全闭环反馈单元之间在回转方向不存在明显的弹性环节,因此C轴工作台可以作为动态检测和精准修正的试验平台。
1.2 插齿加工工艺数学模型
插齿刀坐标系和工件坐标系如图2所示。

图2 插齿刀坐标系和工件坐标系
以O1为原点建立坐标系x1O1y1,该坐标系与插齿刀固连,随刀具旋转,即为插齿刀坐标系。以O2为原点建立坐标系x2O2y2,该坐标系与工件固连,随工件旋转,即为工件坐标系[6],在初始位置时,坐标轴y1、y2与y重合,x1、x2与x平行。插齿机加工齿轮的切削路径在粗加工阶段采用螺旋进给方式,即插齿刀与工件做展成运动的同时,插齿刀向工件中心方向做径向进给运动,以保证切削每个齿时的最大切削力稳定且不大于机床提供的额定切削力;中心距a=O1O2,插齿切削过程中,2个坐标中心逐渐靠近,中心距逐渐变小,当达到切削深度位置时的中心距为最终中心距;当插齿刀相对工件进给到最终径向切削位置时,进入精加工阶段,径向进给停止,插齿刀与工件做展成运动;当工件做一周展成运动后,切削停止,完成切削。插齿加工工艺路径如图3所示。传动比i12为常数,在常规加工切削过程中保持不变。

图3 插齿加工工艺路径
1.3 齿廓线分析
用展成法加工齿轮时,工件齿轮的齿廓由3段曲线构成,齿廓曲线构成如图4所示。
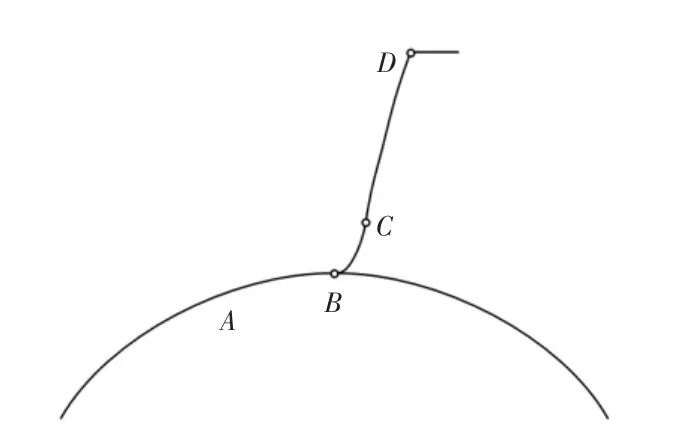
图4 齿廓曲线构成
A-B为齿槽底部的圆弧;C-D为刀具齿轮齿廓的包络线;B-C是连接A-B和C-D的过渡曲线。参与齿轮啮合的C-D曲线段为渐开线,以该线段为主要研究对象。
对于一个齿轮的某一齿,齿两侧为渐开线,齿轮齿槽分析如图5所示。为了便于检测和比较,选择齿轮分度圆和齿中心线的交点G作为检验齿轮误差的参考点[7]。标准齿轮点G处齿轮半径为ZM/2,相邻齿参考点与中心线连线的夹角为2π/Z。

图5 齿轮齿槽分析
2 误差动态检测与补偿
2.1 齿廓数据点云采集
为了进行动态精度检测,在机床本体上安装激光位移传感器,使检测光斑处于工件高度方向的中部且垂直于工件侧面[8-11],激光位移传感器测量齿轮如图6所示。

图6 激光位移传感器测量齿轮
选用Optimet-ConoPoint-3-25N激光位移传感器,该传感器是一种非接触高精度测量距离和三维表面的点传感器。角覆盖达到±85°的复杂几何形状测量,测量精度达1 μm,测量频率达3 000 Hz,可用于本研究测量环境和需求。
将工作台旋转坐标反馈数据与激光位移传感器测得的数据进行即时同步,检测获得的数据在极坐标下表示,包含齿轮半径r和旋转角度θ两个坐标数值,即为工件齿面检测点的坐标;当工件旋转一周,激光位移传感器可以测得工件完整的横截面点云坐标。测量得齿轮点云如图7所示。

图7 测量得齿轮点云示意图
2.2 齿廓曲线拟合
考虑到后续数据处理的需要,对测量结果进行坐标变换,获得直角坐标系下的点云坐标。为了描述齿轮轮廓,需对测得的离散点云数据进行曲线拟合[12-15]。鉴于B样条曲线具有几何不变性、凸包性、保凸性、变差减小性、局部支撑性等特性,选用B样条曲线对渐开线的核心曲线段进行拟合。B样条曲线方程为:
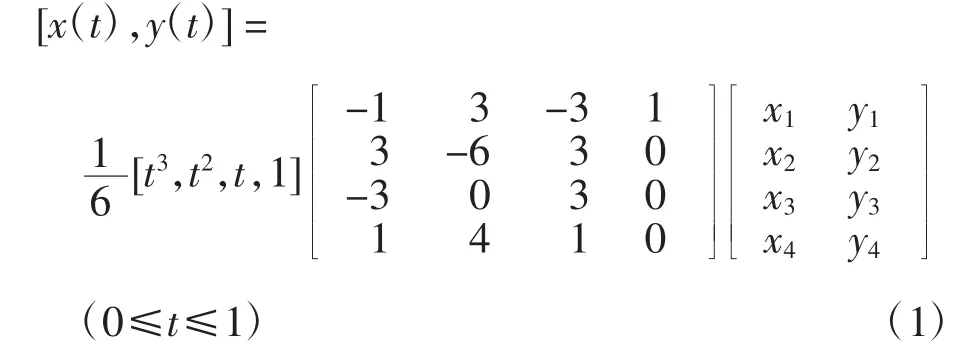
按照B样条曲线拟合原理,渐开线曲线段拟合过程如图8所示。

图8 渐开线曲线段拟合过程
2.3 齿廓误差计算
由拟合曲线计算齿廓两侧2条渐开线的中心线。对每个齿廓进行分析时,以该齿理论位置为基准,计算该中心线与理论齿廓中心线的夹角,进一步计算该中心线与分度圆交点到理论齿廓中心线与分度圆交点的圆弧距离。单个齿廓误差分析原理如图9所示。

图9 单个齿廓误差分析原理
图9中:曲线a、b为通过检测坐标点拟合获得的曲线;曲线c、d为理论齿廓渐开线;l1为2条拟合曲线的中心线;l2为单个理论齿廓的中心线;圆弧AB所在圆为分度圆;G1点为2条拟合曲线的中心线与分度圆交点;G2点为理论齿轮单个齿廓中心线与分度圆交点;圆弧G1G2的距离为实际齿廓与理论齿廓的分度误差δ。
2.4 靶向修正
在切削过程中,将上述检测计算结果进行汇总,将点数据拟合为B样条曲线,在工作台回转轴增加虚拟运动轴,虚拟运动轴以文献[16]曲线表方式运行上述计算结果,虚拟运动轴曲线表示意图如图10所示。横坐标Z为齿数,纵坐标δ为实际齿廓与理论齿廓的分度误差。对工件进行动态切削补偿,达到优化齿距累积公差的目的。

图10 虚拟运动轴曲线表示意图
在对工件进行动态切削补偿的过程中,插齿刀与工件的传动比为非线性比例,常规的匀速齿轮展成成形转变为工件匀速-插齿刀变速展成成形,这种针对齿轮某一项精度指标做修正的方法,即为靶向修正,为了减小误差映射,切削全过程采用靶向修正精准加工技术。
2.5 在线精度检测
在完成最终切削后,进行精度检测,计算拟合后的渐开线与分度圆的交点坐标。齿距测量的结果用于计算单个齿距偏差和齿距累积公差。根据《国家标准GB-T 10095.1-2001》中规定:单个齿距偏差定义为在端平面上接近齿高中部的一个与齿轮轴线同心的圆上实际齿距与理论齿距的代数差;齿距累积公差定义为任意K个齿距的实际弧长与理论弧长的代数差。理论上它等于这K个齿距的各单个齿距偏差的代数和[17-20]。

图11 齿距偏差示意图
用上述计算方法对齿轮检测结果进行检验,将齿距累积公差分别与标准值相比较,如检测结果均低于设定的标准值,则该工件合格。
3 结语
本文提出了以非线性展成为特点的插齿加工靶向修正概念及基于动态检测和靶向修正技术的大型齿轮精准插齿加工方法。该方法利用激光位移传感器实时检测被加工齿轮齿面,生成点云数据,借助B样条曲线对检测数据进行拟合;依据检测计算结果,通过在工作台回转轴增加虚拟运动轴实现齿距误差动态补偿进行靶向修正,提高大型齿轮加工精度;切削完成后可以检测单齿齿距偏差和齿距累积误差,用于对工件加工精度进行在线检测和判定是否合格。本文提出的精准切齿方法能够实现齿轮加工误差的动态检测和补偿,有效提高了齿轮加工精度。该方法不仅有利于大型插齿机加工能力的提升,也适用于中小型插齿机和滚齿机、磨齿机、铣齿机、剐齿机等齿轮加工装备升级改造,具有普适性。研究成果将丰富齿轮加工理论,为工程应用奠定基础。

