双频FTP对复杂三维面型的轮廓检测*

张松松,黄海松,姚立国

(贵州大学 现代制造技术教育部重点实验室，贵阳 550025)

0 引言

双频傅里叶变换轮廓术已经被许多学者做了深入的研究，由于具有全场测量、非接触性、高分辨率、测量精度高的优点，在机器视觉、工业检测、文物保护、三维传感等领域得到广泛应用，近年来，这项技术也被引入到三维物体型面检测和变形测量中，并将其作为工业生产检测中的基本要求[1-2]。

在传统的三维检测应用中，通常利用傅里叶变换轮廓术和数字莫尔法方法来获得表面轮廓的信息，然而，这种方法只是针对一些简单、小高度步长的三维表面物体有较好的检测精度，当被检测的物体具有复杂三维表面轮廓、表面隔离和大步长，测量件存在表面阶跃时，这就要进行相位展开，使用传统的相位解缠过程仍然有很大可能发生2π相位模糊问题[3-5]，因此，在文章中，通过构建光栅模型来检测复杂三维物体模型，并运用双频傅里叶变化轮廓术准确恢复物体面型，解决2π相位模糊问题。

1 基本原理

在具有复杂型面物体的检测过程中，测量包含突变成份的位置时，相位值被包裹在[-π，π]的范围内，传统的高频光栅或者低频光栅检测过程，产生的频谱很可能出现混叠现象，检测不够精确，本文为了求得连续真实的相位分布，结合了低频光栅与高频光栅的优点，通过构建测量模型，同时捕获两帧不同频率的变形条纹图案，运用双频FTP将两者的数据融合，正确提取出真实的相位变化，最终得到物体突变部分的精确轮廓。

2 检测模型的设计与构建

2.1 测量模型

我们所使用的双频(FTP)检测系统光路图如图1所示，使用一台CCD相机在垂直于参考平面上方进行拍照来获取物体表面轮廓信息，并同步到PC端[6]。

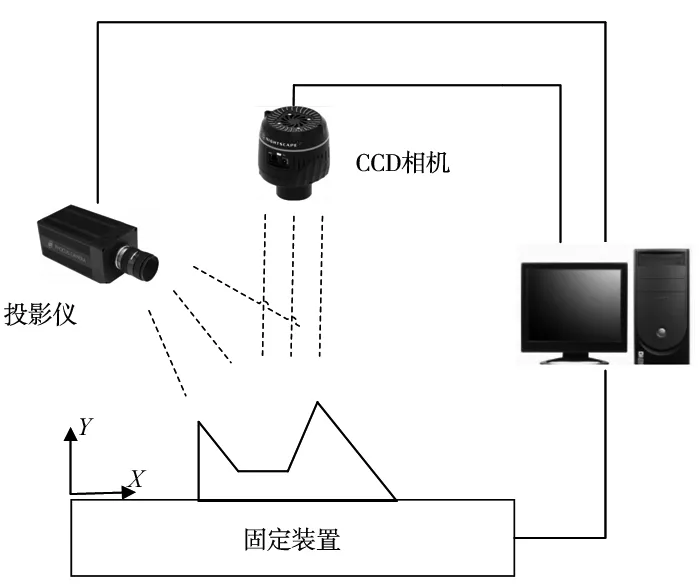
图1 检测系统模型光路图

2.2 测量原理

在大步长复杂三维型面的检测中，关键点就是同时捕捉两帧不同频率的变形条纹图案，我们分别将不同频率的平行数字光栅投射在被测物体上，被检测物体固定在参考平面上，光轴垂直于参考平面，线扫描CCD相机分别两次捕获这两种光栅编码的表面图像，并将拍摄的图像存储在个人电脑中，这样，物体表面上相同点位置就被记录了两次不同频率的条纹图案，这两个条纹图案的帧数是不同的，一组是频较低的条纹图案，一组是频率较高的条纹图案。通过获取两幅图像中物体表面相同点的相应图像强度，并对采集到的图像进行滤波、傅里叶变换等操作，应用双频率FTP提取没有2π相位模糊的实相，最终恢复出三维面型[7]。假设两幅图像中同一表面点的y坐标差为Δy，则两幅图像中一个表面点对应的图像强度可表示为l1(x,y)和l2(x，y- Δy)。 然后分别用傅里叶变换法得到主相位φ1(x,y)和φ2(x,y)[8]，没有2π相位模糊的实相φ2(x,y)可以通过等式(5)和式(7)得到。

在文章实验研究中，CCD相机的分辨率为2048像素，数字投影仪的分辨率为800×600，为了获得无失真的图像，条纹像素为256×256pixel，CCD相机的扫描频率设置为1.64kHz,CCD相机通过个人电脑同步，增益和光圈设置在同一水平，CCD相机获得的不同条纹图像将被存储用于后续处理，条纹图案的间距分别为20mm和55mm。

3 双频FTP检测模型

3.1 基本原理

为了测量大步长、存在表面阶跃的三维物体，我们采用双频FTP进行面型恢复，理论分析如下。

在投影光栅FTP中，由CCD相机记录的强度可以表示为式(1)：

l(x,y)=a(x,y)+b(x,y)cos[2πf0x+φ(x,y)]

(1)

I(x,y)由恒定的高频信号f0调制解调获得，a(x,y)是背景光强，b(x,y)是光栅的振幅，f0是光栅频率，φ(x,y)是由检测到的表面高度引起的相位变化。式(1)经变形得到式(2)[9]：

l(x,y)=a(x,y)+c(x,y)exp(j2πf0x)+
c*(x,y)exp(-j2πf0x)

(2)

其中，c(x,y)= [b(x,y)/2]exp{j[φ(x,y) ] }和c*(x,y)是c(x,y)的复共轭，l(x,y)相对于x的傅立叶变换变为式(3)，其中F[]，A()和C()表示傅里叶谱，C*是C的复共轭。

F[l(x,y)]=A(f.y)=C(f-f0,y)+C*(f+f0,y)

(3)

由于a(x,y) ，b(x,y)和φ(x,y)的频率远低于f0, 函数C(f-f0,y)可以通过频域进行适当滤波得到，C(f,y)可以通过频移中心处理得到，对C(f,y)进行傅里叶逆变换得到c(x,y)，因此，变形后相位关系为式(4)[10]：

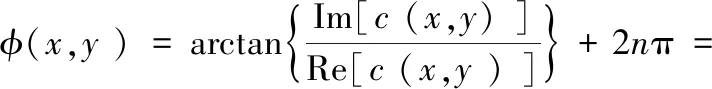
(4)

其中，F=Re[c(x,y)]和G=lm[c(x,y)]分别表示c(x,y)的实部和虚部，φ(x,y)是主相位在(-π,π]的范围内通过相位解缠过程取得的连续实相位分布。

但是，如果该物体在某个地方有一个很大的阶跃高度，2π相位模糊问题仍然可能发生在传统的相位展开处理之后，我们利用双频投影光栅轮廓术可以用来解决这个问题。在测量过程中，分别使用两个不同频率的光栅来获得相位变化，首先将一帧较高频率的数字光栅投射到被检测物体上，从而得到物体表面变化的高斜率信息，其次，将另一个频率较低的数字光栅投射到被检测物体上，表面高度不连续引起的条纹最大变形应小于投影光栅的波长，这样才能正确提取真实的相位变化[11]。

3.2 相位展开算法

假设低频条纹图的光栅频率为f1，相位变化为φ1(x,y)，主相位为φ1(x,y)，高频条纹图案的光栅频率为f2，相位变化为φ2(x,y)，主相位为φ2(x,y)，从而得到式(5)：

(5)

通过使用相同的检测系统，由两种条纹图案获得的一个点的表面高度可以表示如下：

(6)

其中，k1和k2是对应于系统参数的不同条纹图案的两个恒定值，从式(5)和式(6)，我们可以得到式(7)：

(7)

其中，(INT)[]表示四舍五入到最接近的整数，将n2(x,y)代入方程(5)，可以获得没有2π相位模糊的实际相位φ2(x,y)[12]。

4 计算机模拟及结果

实验选用表面具有凹凸形状的待测件，这样可以达到证明双频FTP对大步长复杂形状表面物体检测的可行性。

待测件被固定在装置上，测量基本与单频条纹测量一致，先后获得高低频频条纹图如图2所示，图2a是较低频率条纹图，其中光栅的波长足够长来克服大步长表面高度，图2b是较高频率的条纹图案，从中发现样品表面有一个条纹包裹，图中高低频率条纹频域信息并未发生明显混叠现象。

(a)较低频率条纹图案 (b)较高频率条纹图案 图2 不同频率的变形条纹图案

用检测样品来证明所提出的双频FTP用于解决2π相位模糊问题的可行性，检测样品的横截面示意图如图3所示，样品的底部宽度为250mm，高度为70mm，有一个复杂不连续性表面。

图3 检测件横截面示意图

实验测量系统如图1所示，复合条纹图案由计算机自动生成投射到被检测物体表面，变形的条纹图案分别由CCD相机捕获，利用双频FTP计算出物体表面的三维型貌，实验结果由图4所示，图4a、图4c和图4e分别为采用低频条纹、高频条纹和双频条纹获得的测量件的三维形貌图，图4b、图4d和图4f分别为对应的试件表面的截面图。

比较图4a、图4c与图4e可见，单从低频信息中恢复得到的表面，虽然可以完全展开，但精度较低，平整部分起伏明显，单从高频频率相位展开后的结果看，表面精度有所提高，但是在表面阶跃部分不能精确展开，根据双频FTP相位展开后的结果看，精度明显得到提升，图形表面有了较大的改善。

(a)单独低频条纹的实验结果 (b)低频条纹测量的截面图

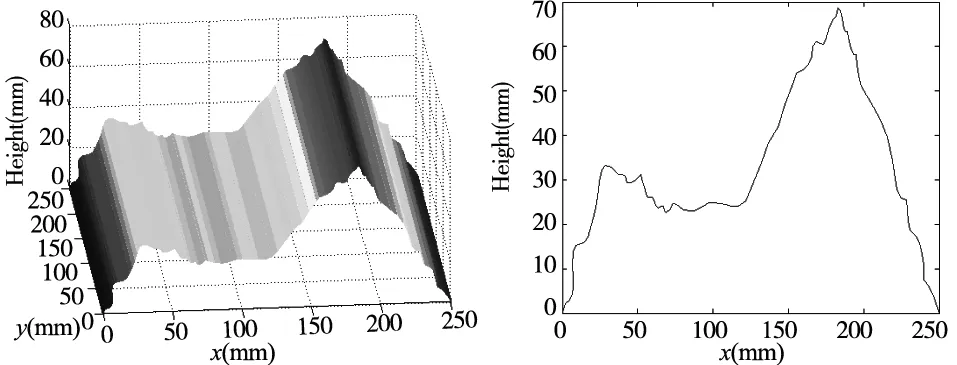
(c)单独高频条纹的实验结果 (d)高频条纹测量的截面图

(e)双频条纹的实验结果 (f)双频条纹测量的截面图 图4 双频FTP实验结果

5 实验分析与结论

从图4所示的实验结果可以发现，低频条纹投影可以获得没有2π相位模糊的表面高度，但是检测精度不够高，尤其是在对应的表面梯度变化较大处测量结果不准确，另一方面，更高频率的条纹投影可以在局部区域提供更高的检测精度，但是测量件存在表面高度阶跃时，该方法获得的相位中依然含有2π相位模糊，然而，双频光栅检测不但可以提高检测精度、获得真实的相位的同时，还能消除2π相位模糊问题，通过计算得到，双频FTP的测量结果表面误差仅为0.2mm。

本文通过采用双频条纹傅里叶变换轮廓术有效地克服了由于大步长、表面阶跃引起的2π相位模糊问题，同时该方法通过捕获不同频率的条纹图案，运用双频FTP原理，提高了复杂三维型面的测量精度，在存在突变成份的三维物体检测中成功地得到三维物体的精确轮廓，从而为工业上复杂三维型面的检测提供了一种更为有效的解决方案。