超声抛光实验平台综合误差建模及补偿方法研究*

于天彪，卞希帅，张 涛，安久贺，赵 继

(1.东北大学 a.机械工程与自动化学院；b.辽宁省高端装备智能设计制造技术重点实验室，沈阳 110819;2.沈阳新松机器人自动化股份有限公司，沈阳 110819)

0 引言

工业的发展离不开高端精密加工设备，随着制造业的高速发展，对加工机床的要求也越来越高。在目前高档数控机床高精度的基础上，通过硬件提高机床的加工精度会大量增加制造成本，机床的精度和制造成本呈几何级数增长。在对机床结构的各误差源进行分析测量之后，依据建立的有效的综合空间误差数学模型，在加工运动的过程之中对各误差源进行补偿修正，从而达到所要求的精度，补偿数控机床刀具和工件间的实际位移可以经济，有效地提高数控加工精度[1-4]。

在多轴机床运动部件多轴联动的情况下，各运动部件的几何误差在实际状态下耦合会产生刀具在空间中相对于理想状态下的位置和姿态上的误差，机床加工刀具的位置误差和姿态误差可以通过机床误差模型计算得出。国内外学者通过对机床几何误差进行广泛地研究，建立了变分模型，D-H模型，多体系统模型等多种误差理论模型。其中多体系统理论[6-10]在研究多体系统问题时具有很强的通用性，也有利于计算机编程进行复杂的计算，对多个刚体联结成的运动体进行抽象和概括，能够有效分析其间复杂的运动学关系。文献[6]中通过多体系统理论建立了工作台回转型的五轴数控机床(工件被固定在两个旋转轴上)的几何误差模型，并利用切割实验对模型进行有效性的验证。文献[8]针对以气浮平台为运动部件的四轴抛光系统，利用多体系统理论，建立了同时考虑位置误差和方向误差的综合误差模型并通过实验揭示了气浮平台产生几何误差的原因，为抛光平台的几何误差补偿提供了理论依据。

为了解决实验室搭建的5轴超声抛光实验平台(工件和工具头分别被固定在不同方向的旋转轴上)上抛光头在空间中位置误差和姿态误差问题，本文基于多体运动学对超声抛光实验平台进行理想运动学正反解建模，分析实际运动中的各运动误差，并对其建立综合误差模型，分析主要误差源，并提出一种误差补偿的方法，提高加工高精度光学复杂曲面[5]的精度和效率。

1 运动学正反解模型

1.1 超声抛光实验平台的运动分析

超声抛光实验平台三维模型建模如图1所示，具有x轴，y轴及z轴三项平动和A和C两项转动。

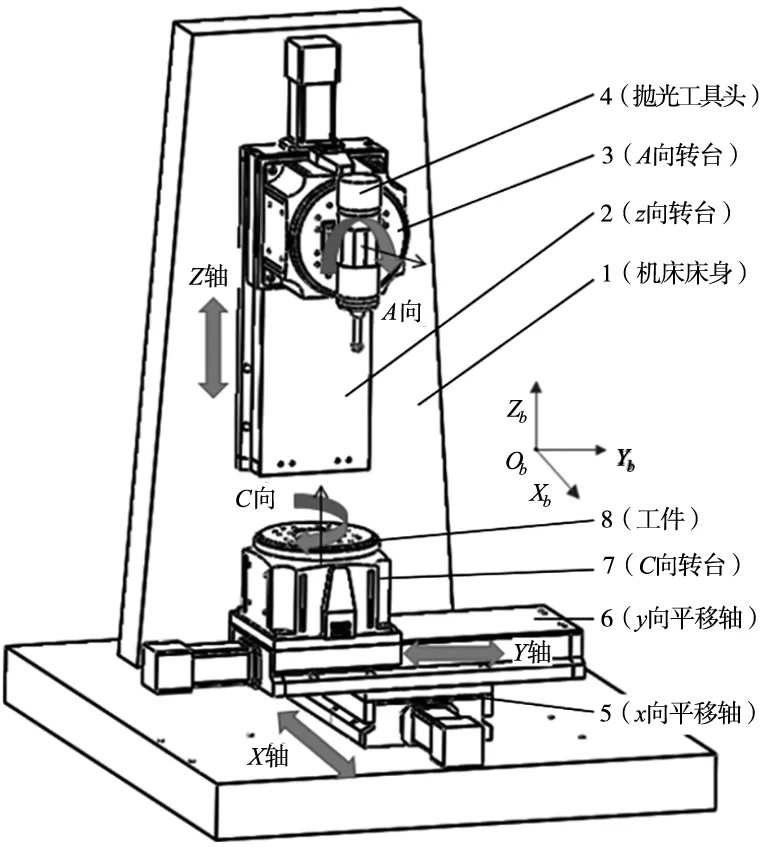
图1 实验平台三维模型

实验平台具有两个开环的运动链：工件运动链和刀具运动链。刀具运动链由机床床身，Z轴，A轴和刀具依次组成，刀具固定安装在A轴上；工件运动链由机床床身开始，x轴，y轴，C轴和工件依次组成，工件安装在C轴工作台上；整体运动链由工件，C轴，y轴，x轴，机床床身，z轴，A轴和刀具依次组成，如图2所示。

图2 实验平台运动链分析

1.2 基于多体系统实验平台的运动学正解模型的建立

根据多体系统理论，将抛光实验平台抽象成一个多体系统，相邻典型体间的运动可以通过齐次变换矩阵来表示，在超声抛光实验平台上对各个体进行标注，并建立相应的右手笛卡尔坐标系，将大地作为B0体，机床床身作为B1体，然后将这些体沿刀具运动链和工件运动链依次标注，实验抛光实验平台的结构示意图和拓扑图如图3所示。

图3 超声抛光实验平台的拓扑图

在超声抛光实验平台的各个体上建立右手笛卡尔坐标系，在机床床身上建立参考坐标系O1x1y1z1，在z向平移轴上建立O2x2y2z2，在A向转动轴上建立O3x3y3z3，依次在各个体上建立坐标系。

1.2.1 理想状态下各相邻典型体间相对静止时的齐次变换矩阵

根据坐标系的建立位置，典型体3和4，7和8之间的坐标系具有相对静止的位姿变换(各相邻典型体的位姿变换均为平动)，典型体1和2，2和3，1和5，5和6，6和7之间的坐标系重合。各相邻典型体相对静止时的齐次变换矩阵。

(1)

(2)

T12p=T23p=T15p=T56p=T67p=I4×4

(3)

式中，d1,d2,d3为实际机床结构中典型体4的坐标系相对于其低序体3坐标系的偏置，d4,d5,d6实际机床结构中典型体8的坐标系相对于其低序体7坐标系的偏置。

1.2.2 理想状态下各相邻典型体间运动的齐次变换矩

阵

(1)z向溜板相对于床身的沿z轴平动z的齐次变换矩阵为:

(4)

(2)A向转台相对于床身的沿x轴转动A的齐次变换矩阵为:

(5)

(3)x向溜板沿x轴平动z的齐次变换矩阵为:

(6)

(4)y向溜板沿y轴平动y的齐次变换矩阵为:

(7)

(5)C向转台沿z轴转动的齐次变换矩阵为:

(8)

(6) 主轴和z向溜板之间，工件C向转台之间的齐次变换矩阵为:

T34s=T78s=I4×4

(9)

1.2.3 运动学正解模型

工件坐标系到刀具坐标系相对于机床坐标系的理想齐次变换为:

IT14=IT12·IT23·IT34

(10)

IT18=IT15·IT56·IT67·IT78

(11)

刀具坐标系相对于工件坐标系的理想齐次变换矩阵为:

(12)

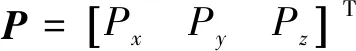
(13)

在实验平台中:

超声抛光实验平台的正解模型为:

(14)

1.3 基于多体系统实验平台的运动学反解模型的建立

根据已经建立的正解运动模型，5轴数控实验平台的刀具姿态的运动学正解可以表示为:

(15)

由式(16)可以解出转动轴的运动学反解A,C

(16)

5轴数控实验平台的刀具位置的运动学正解可以表示为:

(17)

再根据式(16)和式(17)，能够解出平动轴的运动学反解x,y,z:

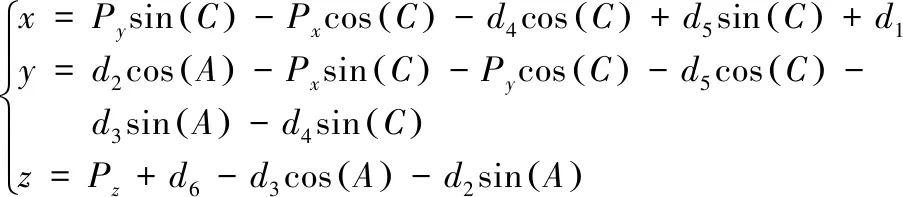
(18)

2 超声抛光实验平台综合误差计算

在实际的加工过程中，各运动部件都会产生和传递误差，设定的刀具的轨迹和姿态会产生一定的偏差，因此，在考虑典型体在实际情况下的位姿时，需要分析理想状态下相邻典型体间的相对静止时存在的垂直度误差源以及实际情况下相对运动中会影响实际刀具位姿的各运动误差源。

2.1 超声抛光实验平台存在的误差源分析

如图1所示，当工件在工作台上绕C向转动时，会产生三项移动误差和三项转动误差[11]，分别为：

当工件在工作台上沿y轴平动时，会产生三项移动误差和三项转动误差，分别为：

同理，当工件在工作台上沿x轴平动时，会存在三项移动误差和三项转动误差；当刀具沿A向转动时，存在三项移动误差和三项转动误差；当刀具沿z轴平动时，会产生三项移动误差和三项转动误差。

另外，相对静止时机床整体还存在3项垂直度误差，分别为Z轴相对于X轴和Y轴的垂直度误差ηyz、ηxz，Y轴相对于X轴的垂直度误差ηxy。为使建模简单，不考虑机床几何误差中的刀具和工件的安装误差以及机床的热变形误差。

对各运动部件的误差进行分析，存在的几何误差如表1所示。

表1 实验平台中的几何误差项

2.2 实际运动学描述

在实际运动中，典型体Bk的姿态在由其低序体Bj通过上图所示的运动变换得到：首先通过给低序体Bj一个理想相对静止的矢量Tjkp，得到一个理想初始位姿，在加上一个相对静止误差矢量ΔTjkp，得到实际初始位姿，其次，依次融入一个理想运动矢量Tjks和一个实际运动误差矢量ΔTjks，最终得到典型体Bk的实际位姿，如图4所示。因此，相邻典型体Bk和Bj之间位置的实际运动齐次变换矩阵可以表达为：

Tjk=Tjkp·ΔTjkp·Tjks·ΔTjks

(19)

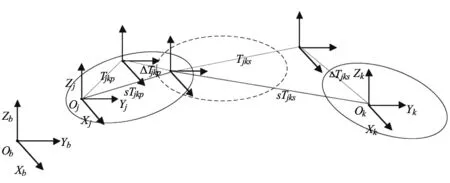
图4 相邻几何体实际运动学描述

2.3 实际状态下各相邻典型体间的误差齐次变换矩阵

2.3.1 相对静止误差齐次坐标变换

(1)z向溜板相对于床身的静止误差齐次坐标变换:

(20)

(2)x向溜板相对于床身的静止误差齐次坐标变换:

(21)

(3)y向溜板相对于x向溜板的静止误差齐次坐标变换:

(22)

(4) 其他各典型体间并无相对误差，其静止误差齐次坐标变换为I4×4。

2.3.2 相对运动的误差齐次变换矩阵

(1)z向溜板相对于床身的沿z轴平动z的误差齐次变换矩阵为:

(23)

(2)A向转台相对于床身的沿y轴转动A的误差齐次变换矩阵为:

(24)

(3)x向溜板沿x轴平动x的误差齐次变换矩阵为:

(25)

(4)y向溜板沿y轴平动y的误差齐次变换矩阵为:

(26)

(5)C向转台沿Z轴转动C的误差齐次变换矩阵为:

(27)

(6)主轴和z向溜板之间，工件和转台之间并无相对误差:

ΔT34s=ΔT78s=I4×4

(28)

2.4 基于工件坐标系的机床综合误差建模

在机床工作加工过程中，刀具坐标系O4x4y4z4相对于机床坐标系O1x1y1z1中的齐次变换矩阵为:

T14=T12T23T34

(29)

机床坐标系O1x1y1z1相对于刀具坐标系O8x8y8z8的齐次变换矩阵为：

(30)

因此刀具坐标系O4x4y4z4相对于工件坐标系O8x8y8z8中的齐次变换矩阵为：

T84=T87T76T65T51T12T23T34

(31)

在实际运动情况下，刀具刀尖相对于工件坐标系的坐标为:

(32)

则工件坐标系下的综合误差模型即为实际加工过程中刀具的轨迹和姿态与理想状态下刀具轨迹和姿态的偏差，即:

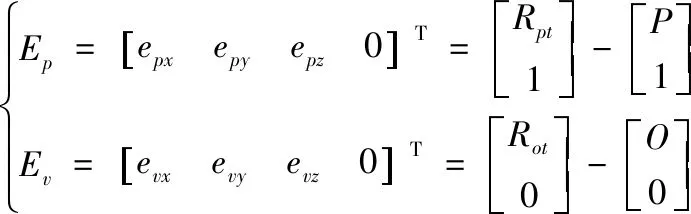
(33)

其中，epx为位置综合误差x向分量，epy为位置综合误差y向分量，epz为位置综合误差z向分量，evx为姿态综合误差x向分量，evy为姿态综合误差y向分量，evz为姿态综合误差z向分量。

3 综合误差的补偿

在获得各轴位置和姿态的综合误差值之后，采用开环前馈补偿控制方法，对五轴抛光机床进行综合误差补偿。在5轴数控机床中，对运动误差进行补偿的难点在于两个旋转轴。平动轴和转动轴同时运动，转动轴旋转的过程中，不仅会产生角度的变换，也会带来位置的改变[12]，即补偿转动轴的误差会在平动轴上产生新的误差，旋转运动和平移运动之间存在着耦合，因此不能仅仅简单地对各轴单独补偿，要综合考虑转动轴所带来的刀具在位置上的变化。

在刀具的运动过程中，平动轴的位移不影响刀具的方向，但刀具的姿态变化会引起刀尖位置的改变，由此，提出一种解耦的补偿方法，即先补偿刀具姿态上的误差，再对位置误差进行补偿，刀具姿和位置补偿过程示意图如图5所示，位姿1是实际刀具所在的位置和姿态，位姿3是理想的位置和姿态，当刀具处于位姿1时，首先通过转动轴对刀具转动一个角度，进行姿态上的调整，刀具运动到和理想刀具姿态相同的位姿2，因为转动轴和平动轴存在着运动上的耦合，需要补偿在旋转一角度后位姿2和理想位姿的新的位置误差，而不仅补偿原有位姿1和理想位姿的位置误差，从而使刀具运动到位姿3，即理想的位置和姿态。

图5 刀具姿和位置补偿过程示意图

具体的补偿方法流程图如图6所示，首先进行姿态上的误差补偿，由输入的刀具命令x、y、z、A、C正解计算出刀具在工件坐标系下的姿态Oi，Oj，Ok和刀具运动的综合姿态误差evx、evy、evz，补偿后得到刀具的实际姿态sOi、sOj、sOk，经运动学反解计算出实际刀具转动量As、Cs。其次，对刀具进行位置上的误差补偿，结合计算出的实际刀具转动量As、Cs和输入的理想刀具命令x、y、z计算出刀具在工件坐标系下的理想刀具位置Px、Py、Pz和综合位置误差epx、epy、epz，补偿后得到刀具的实际位置sPx、sPy、sPz，经运动学反解计算出实际刀具的平动量xs、ys、zs。最后，根据由综合误差计算公式计算补偿后的综合运动误差，判断是否在所规定的误差允许范围内，符合条件输出补偿后的刀具命令。

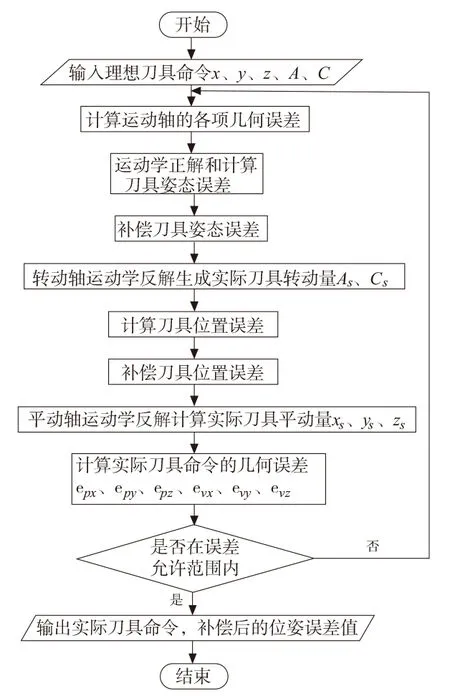
图6 补偿方法流程图

4 仿真实验分析

因本文所述超声抛光实验平台尚未搭建完成，采用文献[9]中所测量的各轴误差数据进行实验分析和补偿效果验证。

根据上述误差测量结果和已建立的综合误差模型，对抛光机床的x，y轴联动及各误差元耦合的情况下进行综合误差的变化规律研究，包括综合误差在x轴，y轴，z轴上的移动误差和转角误差。通过Matlab软件生成实验平台x轴和y轴联动和各误差元耦合情况下综合误差在x轴，y轴，z轴轴向上的移动误差和转角误差分量的变化规律，如图7所示。

ex和Δεx在y轴平动过程中的变化较小，在x轴平动过程中变化幅度较大，且成增大趋势；ey和Δεy在x轴平动过程中的变化较小，在y轴平动过程中变化幅度较大，且成增大趋势；ez在x和y轴平动过程中的变化起伏。经过上述补偿流程之后，综合误差如图8所示。

(a)综合误差x向 移动分量 (b)误差分量y向 移动综合 (c)误差分量z向 移动综合

(d)综合误差x向 转动分量 (e)误差分量y向 转动综合 (f)误差分量z向 转动综合 图7 综合误差分析

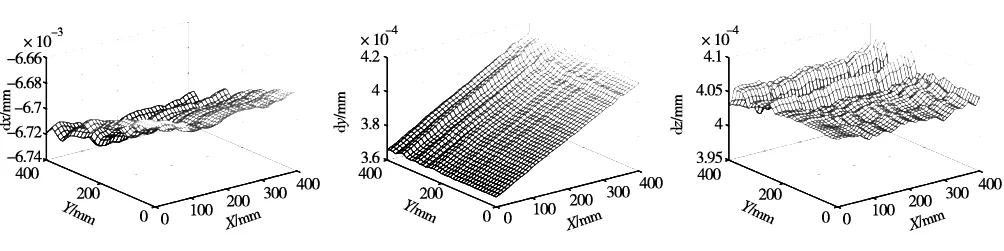
(a)综合误差x向 移动分量 (b)误差分量y向 移动综合 (c)误差分量z向 移动综合

(d)综合误差x向 转动分量 (e)误差分量y向 转动综合 (f)误差分量z向 转动综合 图8 补偿后的综合误差分

由上述实验结果分析可知，经过补偿之后，综合误差ex的误差范围由-1.73～18.25μm降低到-6.67～-6.73μm，综合误差ey的误差范围由-2.17～29.47μm降低到0.365～0.418μm，综合误差ez的误差范围由-6.65～3.71μm降低到0.399～0.408μm，线性误差的误差补偿效果明显，转动误差的差值均为纳米级误差，相对于线性直线度误差可忽略。

5 结束语

采用多体系统理论建立了五轴抛光实验平台的运动学模型和综合误差模型；

提出了一种先补偿刀具姿态上的误差，再对位置误差进行补偿的解耦补偿方法；

对超声抛光实验平台x轴和y轴联动情况下的综合误差进行建模分析和补偿效果进行了仿真实验验证，线性误差降低了60%以上，补偿效果显著。