供应链合作广告的改进及最优策略

方卫国 张晓明 杨琛

（北京航空航天大学 经济管理学院 北京 100191）

一、引言

Roman和Maas[1]在研究广告对销售量的影响时发现，任何产品的销售量都不是无限大的，而是有一个“临界销售量”和“最大可能销售量”。“临界销售量”指某一品牌产品在没有任何广告情况下，只要确实有价值，总会产生一定程度的销售。“最大可能销售量”指某一品牌产品销售量，由于受到产品自身的限制，比如产品质量和生命周期，以及外界环境的影响，诸如市场和经济环境、替代产品和新产品的威胁等，在达到市场饱和或者说一个最高销售点后，就很难甚至无法在销售量上有所增长了。在“临界销售量”和“最大可能销售量”之间的区域，广告可以发挥促销作用。合作广告一般分为纵向（垂直）和横向（水平）合作广告。纵向合作广告指在供应链中，具有纵向关系的两个企业（比如百事可乐和肯德基）合作，用战略合作和联合广告的方式共同宣传二者的产品。而横向合作广告指在市场上横向的两个企业（比如宏碁和IBM），甚至是跨行业的两个企业,为了争取更低廉的价格和其他更优厚的待遇而合作，两家企业同时与同一家广告公司签订合作宣传协议。目前绝大多数行业都存在纵向合作广告，它是许多企业营销战略中极为重要的一环。纵向合作广告中，制造商会为零售商支付部分广告成本。本文研究的合作广告指纵向合作广告。

合作广告一般是由制造商的品牌广告（又叫全国性广告）和零售商的地方性广告组成[2]。全国性广告指制造商在全国市场进行宣传来推广产品，目的主要是建立良好的品牌形象和声誉，让消费者建立对品牌的信任，考虑购买该品牌产品。地方性广告指零售商在其所属地域进行的宣传和促销，目的是提供给顾客更为详细的信息，如去哪里买、怎么买、折扣能有多少等，以此来鼓励和引导顾客的购买行为，较为典型的地方性广告有产品陈列展台、产品促销宣传和商场的宣传活动等。通过合作广告对品牌的营造和对产品购买信息的描述，当顾客有购买该产品的需求时，可以轻而易举获得更全面的信息。而如果只有全国性广告，顾客仅仅知道品牌，却无法了解购买渠道，面临着找不到商店位置等“最后一公里”问题。因此，无论是全国性的品牌广告还是零售商的地方性促销宣传，对提升销售量都有不可忽视的作用。

合作广告作为供应链协调的手段，其对供应链绩效提升的价值，近年来重新受到了关注[3-5]。Aust和Buscher[6]的综述对各种不同的合作广告形式进行了梳理，重点讨论有关纵向合作广告的研究进展，包括静态和动态场景以及研究中采用的各种需求和费用函数。合作博弈和非合作博弈模型在合作广告研究中获得了广泛的应用。Jorgensen和Zaccour[7]对合作广告研究中的博弈模型进行了分类和讨论。除了研究合作广告自身对供应链协调的作用外，进一步将合作广告与订货策略结合起来[8-10]，或者更多地同时考虑合作广告与价格策略[11-16]，研究它们对供应链协调的交互作用。对合作广告的研究，已经从由一个制造商和一个零售商组成的简单供应链结构，发展到由多个制造商或/和多个零售商组成的复杂供应链结构[17-23]；从单周期决策扩展到多周期决策[24,25]。绝大部分研究聚焦在纵向合作广告，也有少量研究探讨横向合作广告问题[26,27]。近年来，随着电子商务的兴起，双渠道供应链的合作广告问题逐渐获得了学者的关注[5,28-30]。

本文考虑由一个零售商和一个制造商组成的、提供单一产品的二级供应链，针对现有的合作广告销售反应函数假设存在的缺陷予以改进，构造新的销售反应函数。基于改进的销售反应函数，研究合作广告的最优策略问题。将制造商作为领导者而零售商作为追随者的合作广告问题，建模为Stackelberg主从博弈。通过求解模型的均衡解，确定制造商和零售商的合作广告最优策略。对博弈均衡及最优策略的相关性质进行理论分析，通过数值模拟对理论分析的结果进行验证。

二、合作广告销售反应函数

Huang和Li[2]认为产品销售量S，受零售商地方性广告水平a和制造商全国性品牌投资q的双重影响，并将期望的销售反应函数假设为如下形式：

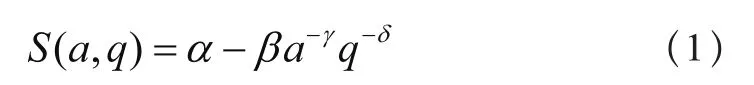
其中α＞0为销售饱和渐近线，即最大可能销售量；β、γ和δ为大于0的常数，γ或δ越大，表明零售商地方性广告投入或制造商全国性广告投入（品牌投资）对销售反应量的影响越大。这一销售反应函数在合作广告研究中被众多学者广泛采用。但上述假设存在四个缺陷：

（a）不能考虑零售商或制造商在广告上不投资的情形。若α=0或q=0，则（1）式没有意义。

（b）对于某些参数组合，如α或q小于1而γ或δ大于1时的某些参数组合，销售反应函数可能出现负值。针对这一缺陷，Ahmadi-Javid和Hoseinpour[31]对销售反应函数已经做了改进。

（c）（1）式隐含着零售商和制造商各自在广告上的投资彼此具有替代效应。当α很小而q→∞，或当q很小而α→∞时，S→α。这意味着仅凭零售商或制造商单方面的广告促销努力，即可使销售量接近饱和。事实上，如前所述，零售商地方性广告与制造商全国性广告具有不同的目标和作用，可以互相促进但不能彼此替代。

针对（1）式所描述的销售反应函数的缺陷，本文提出改进的销售反应函数，它具有如下的Logistic函数形式：

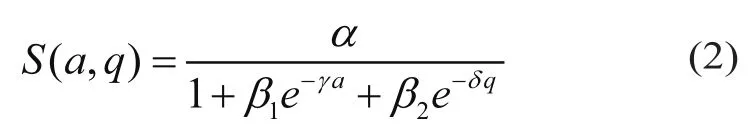
（2）式中，参数α，a，q的含义同前。β1和β2是正常数，分别表征零售商和制造商的促销行为对市场需求的影响力，它们的值越大，表明促销行为对市场需求的改变效果越显著。0〈γ，δ〈1分别为销售量对零售商地方性广告和制造商全国性广告投资的弹性因子。

改进的销售反应函数具有以下性质：

（1）当a→∞且q→∞时，S(a,q)→α，销售量达到饱和。

（2）当a→0且q→0时，。此时的销售量即为在没有任何广告的情况下产品的临界销售量[1]。

（3）当a→0且q→∞时，；

（4）当a→∞且q→0时，。

进一步作出如下两个假设：

（1）弹性因子γ越大，表明零售商地方性广告对销售量的激励越强烈。同样δ的值越大，制造商全国性广告对销售量的激励越强烈。由于制造商全国性广告的影响范围和影响程度，要高于零售商地方性广告的效果，因此，我们假设δ＞γ。

（2）影响力系数β1越大，表明零售商的促销行为对市场需求的影响力越大。类似地，β2越大，表明制造商的促销行为对市场需求的影响力越大。由于制造商促销行为的影响范围和程度要大于零售商，因此，我们假设β1＞β2。

定义其他一些变量：制造商销售每单位产品的边际利润为ρm；零售商的边际利润为ρr；制造商分担一部分零售商的地方性广告费用，设分担率为t，令0〈t〈1。这也可理解为制造商在合作广告中对零售商的补贴。

基于上述假设和变量定义，可得制造商、零售商的利润分别为：

三、合作广告的Stackelberg博弈模型

在传统的产品分销渠道中，由于单个零售商销售量占某一制造企业产量的比重不大，制造商依赖自身雄厚的资金实力和强大的生产能力，在与零售商的对话中往往占据主导地位，能够通过控制某种规格产品的供给对零售商施加影响。为了取得某型号产品的销售权，零售商须要与制造商进行谈判，甚至做出必要的让步。本文考察这种经典的制造商作为领导者而零售商作为追随者的序贯非合作博弈情形，也就是Stackelberg主从博弈，这个博弈的最优解称为Stackelberg均衡。

对于所研究的制造商—零售商合作广告问题，Stackelberg博弈可描述为：合作广告的动议来自零售商，它为了增加自己的广告预算并且在促销方面少花费自身资金从而向制造商寻求帮助。从制造商角度看，零售商通常在地方性广告上的支出比需要支出的数量少。制造商通过采用合作广告补贴策略，诱使零售商增加它的地方性广告支出到某个水平，从而引起产品销售额外增加。而零售商地方性广告支出水平的确定，依赖于制造商愿意支付多少补贴。制造商作为领导者首先宣布其品牌投资水平、合作广告策略；零售商作为追随者，随后决定从正在考虑地方性广告支出预算的制造商处购买产品的数量。换句话说，零售商把地方性广告支出的Stackelberg均衡考虑进来以决定要订购的产品数量。另一方面，制造商考虑零售商的行为，并通过确定品牌效应投资水平和合作广告补偿策略来最大化自身的利润。

制造商—零售商合作广告问题的Stackelberg博弈模型表达为

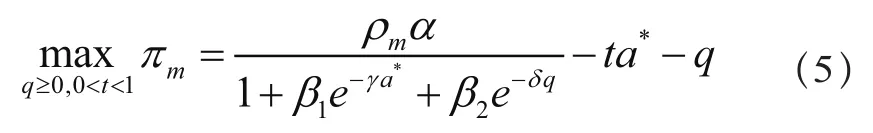
（5）式中，

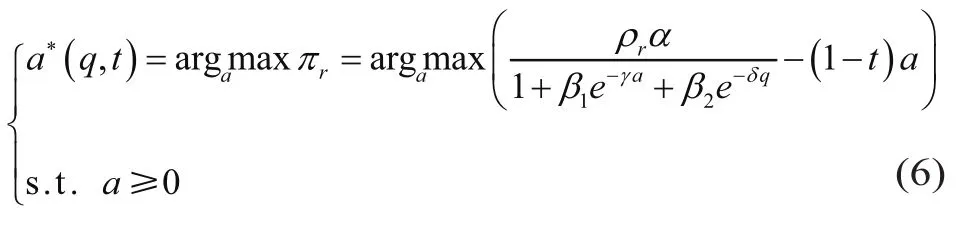
四、Stackelberg博弈均衡求解

为了确定Stackelberg均衡，需要求出这个博弈第二阶段的反应函数。考察πr对a的一阶和二阶偏导数：

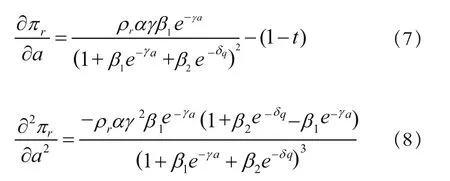
在对a的取值范围不做限定的情况下，无法判断（8）式小于0，因此不能直接通过驻点条件，即令，求出使零售商利润最大的地方性广告水平a*。图1示出了 随a的变化趋势。事实上，当a→-∞时，πr→∞。

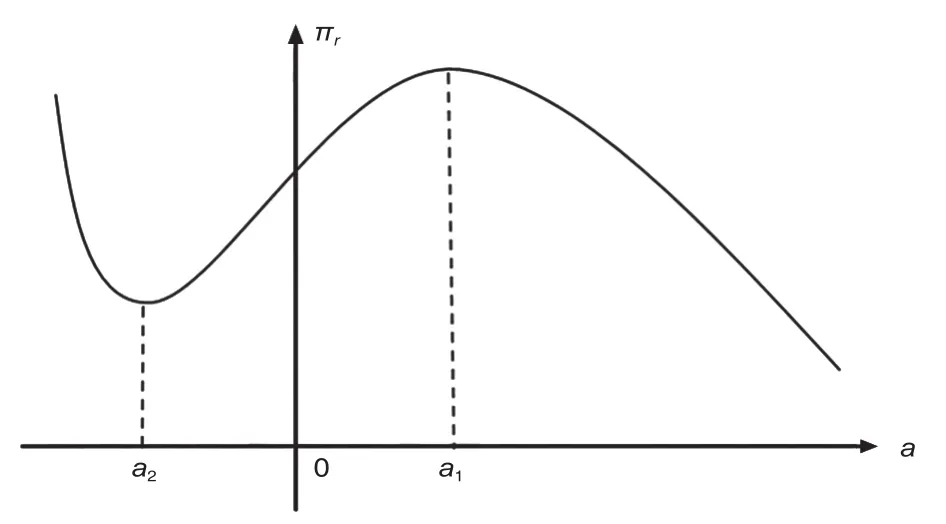
图1 πr随a的变化（ 图片）

考察πr对a的驻点。为简化表达，令β1e-γa=z，pr=ρrαγ，求解方程 (7)，得到

图1 显示，πr有两个驻点a1和a2，a1＞a2，且a1是极大值点。由于0〈γ〈1，故z为a的减函数，则a1对应的z为：

据此可求出零售商最优的地方性广告水平：

以下分析零售商最优的地方性广告水平a*的性质。

（1）计算a*对q的一阶偏导数，得到

分析（11）式，不难判断

和

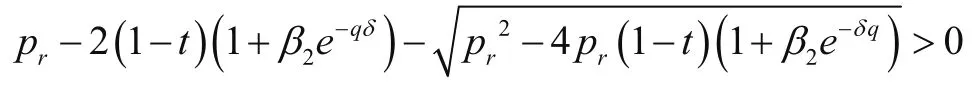
（2）计算a*对t的一阶偏导数，得到

显然，由于t〈1，故。这表明，制造商愿意分担地方性广告费用越多，零售商将愿意在地方性广告上的支出也越多。因此，制造商的合作广告补贴策略也可作为零售商地方性广告支出的指示器，制造商能使用这种指示器来诱使零售商增加地方性广告支出从而达到制造商期望的水平。

下一步，求解Stackelberg博弈第一阶段的优化问题（5），确定制造商最优的全国性广告投资水平q*以及对零售商地方性广告投资的最优分担率t*。将a*的表达式（10）代入制造商利润表达式（3），并令pm=ρmαδ，从而将制造商的利润表达式改写为

根据（13）式，可以推导出

理论上，若πm关于q和t的Hesse矩阵在集合 {(q,t)|q≥0,0＜t＜1 上负定，即πm是q和t的凹函数，则通过求解由组成的非线性方程组，得到πm的驻点。进一步考察驻点确定q*和t*。对于非线性方程组，驻点一般有多个。比较各驻点对应的制造商利润，最大利润所对应的驻点，就是所要寻求的q*和t*。由于πm是q和t的复杂非线性函数，其梯度矩阵及Hesse矩阵的表达式均十分复杂，难以得到q*和t*的解析表达式，只能通过数值方法求解。一旦q*和t*确定，就可根据（10）式计算零售商地方性广告最优投资水平a*。

五、数值模拟

参数假设：饱和销售量α=100；零售商与制造商促销行动对市场的影响力系数分别为β1=1，β2=2；销售量对地方性广告和全国性广告的弹性因子分别为γ=0.2，δ=0.3 。由于制造商占主导地位，它将获得供应链大部分收益。设制造商和零售商的边际利润分别为ρm=2和ρr=0.6。

在这组参数设置下，根据（2）式，若制造商和零售商均不做广告，则销售量仅为25，此即为该产品的临界销售量；若仅有制造商开展全国性广告促销，销售量最多可提升到50；若仅有零售商开展地方性广告促销，销售量最多可提升到33.3。

为开展数值模拟，首先根据销售反应函数，确定全国性广告投资水平的合理范围。令a=0，即假设零售商不开展地方性广告促销活动，仅靠制造商全国性广告刺激销售。此时，销售反应函数退化为。图2给出了销售量随q的变化。当q＞20，销售量的增加已非常微弱，因此在数值模拟中，为简化分析，将q的上限设为20。

图2 销售量随q的变化（a=0）

给定制造商全国性广告投资水平q=12，根据(10)式可绘制零售商地方性投资水平随分担率的变化曲线，如图3所示。根据(4)式可计算零售商和制造商利润随分担率的变化，见图4。

图3 零售商地方性广告水平a随t的变化（q=12）

图4 零售商与制造商利润随t的变化（q=12）

给定分担率t=0.3，根据(11)式可绘制零售商地方性广告水平a随q的变化曲线，见图5。零售商和制造商利润随q的变化见图6。

图5 零售商地方性广告水平a随q的变化（t=0.3）

图6 零售商与制造商利润随q的变化（t=0.3）

图3和图5表明，零售商地方性广告水平a随制造商的全国性广告水平q以及制造商对地方性广告费用分担率t的提高而提高，这与前面的理论分析一致。比较图3和图5，还可以发现，零售商地方性广告水平对分担率的灵敏度，要高于对制造商全国性广告水平的灵敏度。例如，固定q=12，t从0.3增加到0.4，增加率为33.3%，相应地，a从12.995增加到13.872，增加率为6.75%；固定t=0.3，q从12增加到16，增加率也为33.3%，而a从12.995增加到13.391，增加率为3.05%。这说明，比较而言，为诱导零售商将地方性广告提升到期望的水平，制造商提高分担率比提高全国性广告水平更有效。另一方便，通过类似的分析，从图4和图6可以得出，比较而言，零售商和制造商利润对全国性广告水平的灵敏度要高于对分担率的灵敏度。这是因为利润的主要影响因素为产品的销售量，全国性广告水平q直接影响销售量，而分担率只能通过作用于地方性广告水平a间接地影响销售量。这说明，为提升制造商及零售商的利润，制造商要更精心地规划其在全国性广告上的投资水平。

下面确定制造商的最优决策（q*，t*）。由于没有解析表达式，为简化分析，我们对q和t进行离散化，采用数值方法计算。q的取值从0开始，按0.1的步长增长到20；t的下限设定为0.01，按0.01的步长增长到0.99。按（13）式编程计算在不同（q，t）组合下制造商的利润，见图7。得到制造商最大利润π*m=164.5，对应的最优决策为q*=15.8，t*=0.42。

图7 制造商利润随q和t的变化

相应于制造商的最优决策，由（10）式可计算出零售商的最优决策a*=14.4423，零售商利润π*r=47.5，此时供应链销售量达到S=93.185，接近饱和销售量。

六、结 语

本文研究由一个零售商和一个制造商组成的、提供单一产品的二级供应链纵向合作广告最优策略问题，其中零售商要确定其在地方性广告上的投资水平，而制造商要确定其在全国性广告上的投资水平以及对零售商地方性广告费用的分担率。产品的销售量由地方性和全国性广告的投资水平共同决定。分析了当前在合作广告研究中广泛采用的销售反应函数假设存在的缺陷。针对这些缺陷，对销售反应函数进行改进，提出了一种新的销售反应函数。基于改进的销售反应函数，探讨合作广告的最优策略问题。对制造商作为领导者而零售商作为追随者的合作广告最优决策问题，本文将其建模为Stackelberg主从博弈，建立了Stackelberg博弈模型。对模型的求解进行了探讨，对博弈均衡及相关性质进行了理论分析。通过数值模拟，对理论分析的结果进行了展示和验证。数值模拟还发现，对处于领导地位的制造商而言，为诱导零售商将地方性广告投资提升到期望的水平，制造商提高分担率比提高全国性广告投资水平更有效；为提升制造商及供应链的整体绩效，制造商要更精心地规划其在全国性广告上的投资水平。未来进一步的研究，将考虑定价策略与合作广告策略的交互作用对销售量的影响。