基于复合控制的自行车机器人平衡控制

李艳 王涵

关键词： 自行车机器人; 平衡控制; 复合控制; 不稳定零动态; 控制器; 鲁棒性

中图分类号： TN344?34; TP273                 文献标识码： A                    文章编号： 1004?373X（2019）02?0177?06

Balance control of bicycle robot based on compound control

LI Yan， WANG Han

（Shaanxi University of Science and Technology， Xian 710021， China）

Abstract： A compound control method is put forward to realize balance control of the bicycle robot. The bicycle is regarded as a multi?body system， and the system dynamics model is established according to the Lagrange equation. In allusion to the unstable zero?dynamics characteristic of the bicycle robot， the unstable subsystem of the system is used as the inner ring， and the quadratic performance index optimal controller is used for stabilization by means of compound control. In allusion to the disturbance and model uncertainty， the robust controller is designed for the external loop taking the output as feedback， which makes the whole system have strong robustness. The simulation results show that the proposed method can achieve balance control of the bicycle， make the system have the capability of suppressing interference， and ensure the robust stability of the system.

Keywords： bicycle robot; balance control; compound control; unstable zero?dynamics; controller; robustness

0  引  言

自行车机器人作为一种无人驾驶的双轮智能交通工具，具有运动灵活、能源利用率高、绿色环保等特点，使得其在安保巡逻、躲避交通拥堵等领域具有独特的优势和应用前景。由于其复杂的动力学特性，自行车机器人是检验控制策略的理想实验平台，因而其平衡控制问题引起国内外学者的广泛关注[1]。

倒立摆[2]和无人机[3]也都是较为复杂的平衡控制平台。倒立摆可以通过在摆杆倾倒面内施加恢复力矩实现平衡控制;无人机可以在倾斜面内产生空气动力，进而实现平衡控制。相比于上述系统，自行车作为多刚体系统，重心较高，车体狭长，靠前轮摆动和地面的反作用力[4]来实现平衡。此外，自行车机器人的欠驱动[5]和耦合特性会引起非最小相位特性[6]，即不稳定零动态，反映了系统内部动态的发散，该特性对系统的鲁棒性十分不利，这使得其平衡控制更加困难。

针对自行车的以上问题，在控制算法方面，自行车作为自然不稳定系统，更容易受到外界环境的干扰，加之其模型的不确定性，提高系统鲁棒性是一项十分重要的任务。综合国內外文献，现有的提高自行车平衡控制系统鲁棒性的控制算法有执行器容错控制[7]、倾角扰动观测器[8]、基于粒子群优化的[H∞]回路算法[9]以及基于自适应评价的神经模糊算法[10]等。上述这些控制算法结构复杂并且难以实现，其中控制算法[7，9]借助了惯性轮，更增加了系统的复杂程度，并且现有的控制算法对于自行车机器人不稳定零动态的研究也非常少，没有考虑内动态的发散会导致系统的不稳定。文献[5]采用部分反馈线性化，将车架横滚角作为内部动态，保证了零动态的稳定，但此方法需要系统具有精确的数学模型。因此，本文通过控制自行车车把的转角实现系统的平衡，将自行车机器人看作不稳定零动态系统，所设计的控制器既要实现外部动态的渐近稳定，又需保证不稳定内部动态的收敛[6]，宜采用复合控制[11]来提高系统的稳定性和鲁棒性。该复合控制系统中内环采用二次型性能指标最优控制器镇定不稳定子系统，基于自行车机器人的未建模动态、参数变化和外部干扰等原因，外环采用鲁棒控制镇定整个系统，提高系统的抗干扰能力，使整个系统具有鲁棒性，设计的物理概念清晰，便于实现。

1  自行车机器人动力学模型

1.1  模型建立

自行车机器人结构简图如图1所示。

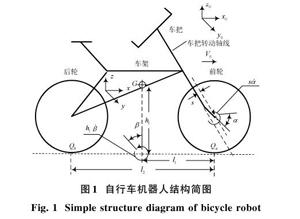
自行车前轮与后轮着地点的连线[Qa][Qb]为自行车坐标系的[x]轴，它偏离惯性坐标系[x0]的角度，即车把转角[α]，[β]为自行车坐标系[z]轴偏离惯性坐标系[z0]的角度，即车体横滚角。自行车以速度[V0]匀速前进，运动过程中用前轮摆角产生的扭转力矩来维持受到扰动后车体的平衡，自行车机器人的非线性动力学模型为[12]：

式中：[mq]，[mh]，[mj]，[md]分别为自行车前轮、后轮、车架、电池质量;[rq]，[rh]分别为前轮、后轮半径;[s]为前轮质心到车把转动轴的距离;[h1]，[h2]分别为车架重心高度和电池重心高度;[l1]为前轮着地点到自行车重心在[x]轴上的距离;[l2]为两接触点连线的距离。

定义状态变量[x1=α，x2=α，x3=β，x4=β]，系统在可控制平衡条件下，车体横滚角不会太大，即[sin β≈β]，[cos β≈1]，[ββ≈0]，经过近似化处理，经矩阵变换后，线性状态空间模型为：

[x=Ax+Bu=010000a1b21-a1b10000100b21-a1b10x+      0a31-a1b1      0a3b11-a1b1u]

[y=Cx+Du]    （2）

式中：

[a1=-mqrqs+mjh1sp12mqr2q+mqs2+mjs2p2，][a3=112mqr2q+mqs2+mjs2p2，b1=-2（mqrqs+mjh1sp）3mqr2q+3mhr2h+4mjr21，][b2=2（mqrqs+mhhh+m0h1+mdh2）g3mqr2q+3mhr2h+4mjr21]

系統各刚体的参数如下：自行车前轮质量[mq]为0.75 kg，半径[rq]为0.14 m，前轮质心到车把转动轴的距离[s]为0.02 m;后轮质量[mh]为1.05 kg，半径[rh]为0.17 m;车架质量[mj]为12.1 kg，车架重心高度[h1]为0.36 m;电池质量[md]为1.4 kg，电池重心高度[h2]为0.66 m。

将上述参数代入式（2），模型数值化后的结果为：[A=010000-94.206 4000010016.972 20，B=       0119.623 2       0    -1.9] （3）

1.2  性能分析

对系统进行欠驱动特性分析。将式（1）写成如下表达形式：

[D（q）q+C（q，q）q+G（q）=τ] （4）

式中：[Ddij2 ×2]为系统的惯性矩阵;[Ccij2×2]为与哥氏力相关的项，且[dij]，[cij（i，j=1，2）]为[α]，[β] 的函数;[G（q）]为重力项;[q=（α  β）T]和[τ=（u  0）T]分别为关节变量和关节驱动力矩，且[u]对应车把转动关节，由于车速是常数，不考虑后轮转动关节。

由式（3）知，自行车机器人为具有两个独立自由度的欠驱动系统，且车架横滚角没有驱动。

自行车机器人作为欠驱动自然不稳定系统，其功能的实现比一般机器人系统困难，而系统的非最小相位特性是由欠驱动和耦合特性引起[6]，接下来分析系统零动态的稳定性。

将式（2）变为如下动态：

[Σ1：x1=x2，x2=-94.206 4x3+119.623 2u，y=x1Σ2：x3=x4，x4=16.972 2x3-1.9u] （5）

通过控制输入，使指定的系统输出恒为零，这时系统的内部动态即为零动态

[x3x4=01 15.475 90x3x4] （6）

零动态中的不稳定极点为3.933 9，则系统的零动态不稳定。

对于自行车机器人这一不稳定零动态系统，宜采用复合控制。式（5）的第一个方程描述了输入/输出之间的外部动态动关系，由于式（5）的第二个方程是不稳定子系统，不稳定极点为4.12。略大于不稳定零动态的不稳定极点。而子系统第二个方程完全可控，所以可以被镇定。

由于自行车机器人的自然不稳定特性，使得自行车的工作环境，如路面颠簸、空气条件刮风下雨等会对自行车系统产生干扰;自行车机器人的模型不确定性不仅体现在系统参数的变化，而且还包括系统的未建模动态特性：一是模型线性化引起的不确定性;二是自行车各个组成刚体部分的参数误差造成的不确定性;三是自行车前叉带动前轮旋转与车体倾斜之间的耦合造成的不确定性。

利用一个非结构化的集合来描述，常用的是乘性不确定性的描述方法，来描述模型不确定性，采用一般的鲁棒控制设计外环控制器。

2  控制器的设计

2.1  不稳定子系统控制器的设计

对于不稳定子系统，设计二次型性能指标最优控制器。

系统的性能指标为：

[J=120∞（xTQx+uTRu）dt] （7）

式中：[R]为正定实对称常数矩阵;[Q]为半正定对称常数矩阵。取二次型指标最优控制器的参数为[R=1，Q=0001]。子系统完全可控，计算可解得最优反馈矩阵[K=[-17.865 5-4.450 4]]，以及唯一的最优控制[un=-R-1BTPx]，即内环的控制输入为[un=-kx3]，达到最优性能指标。其中[P]是Riccati代数方程的唯一解，[x3]表示自行车横滚角，不受控制输入直接驱动，是非自治的、耦合着外部动态。

2.2  鲁棒控制器的设计

采用一般的鲁棒控制即S/KS/T混合灵敏度问题的[H∞]设计外环控制器。

复合控制率为[u=un+uw]，从外环控制输入到系统输出[y=x1]的传递函数为：

[P（s）=119.62（s-3.934）（s+3.934）s2（s+3.278）（s+5.178）] （8）

与等式（6）有相同的不稳定零动态，但已经没有不稳定模态。

S/KS/T问题是指求解以下的[H∞]优化设计问题，即解[minkstabW1SW2KSW3T∝≤γ]的优化设计问题。[S]为灵敏度函数，[T]为补灵敏度函数。

[W1（s）]反应了灵敏度函数的特性，在设计中要求灵敏度函数尽可能得小，这样才能保证减小跟踪误差，有效地抑制干扰的影响，取：

[W1（s）=0.008 163 （s+85）s ] （9）

引入加权函数[W2（s）]，可以限制控制量的大小，防止系统在实际过程中产生严重的饱和现象以及控制量过大而造成执行器的损坏。取：

[W2（s）= 0.000 45] （10）

[W3（s）]表示自行车模型乘性不确定性的上界，反映了补灵敏度函数的特性，[W3（s）]可取对角的非真有理函数，但必须保证[W3G]是真实有理数，受[W3（s）]的分子高于分母的次数这一条件的限制，取：

[W3（s）=0.002 s] （11）

由此解得[H∞]控制器为：

[K（s）= -1 676.7s （s+3.278） （s+5.178）   （s+532.4）  （s+3.934） （s2 + 30.11s + 839.2）]   （12）

最后对所设计的[H∞]控制器进行性能检验。

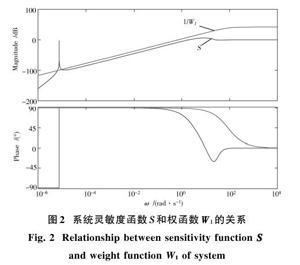
图2为系统灵敏度函数[S]和权函数[W1]与频率[ω]关系的奇异值曲线。[W1S]代表对系统性能的要求，应满足[W1S∝<1]这一必要条件，从图中可以看出[σ[S（jω）]<σ[W-11（jω）]]，所设计的控制器满足系统性能的要求。

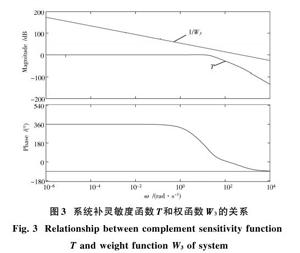
图3为系统补灵敏度函数[T]和权函数[W3]与频率[ω]关系的奇异值曲线。[W3T]代表对系统鲁棒稳定性的要求，应满足[ω3T∝<1]这一必要条件，从图中可以看出[σ[T（jω）]<σ[W-13（jω）]]，所设计的控制器满足系统鲁棒稳定性的要求。

对于控制器设计的合理性，图4为控制器的频率特性，在[ω=4×10-6 rad/s]的频率点附近突然下凹的低增益，该低增益可以有效地抑制干扰的影响。控制器[K（s）]的零点与被控对象[P（s）] 的极点相同，在组成系统时两者发生对消，从而实现了系统的极点的重新配置，保障了系统的鲁棒稳定性。

通过对加权函数及控制器的理论分析可見，混合灵敏度优化问题既考虑了系统性能的要求，又保证了系统鲁棒稳定性的要求，所以本文设计的控制器满足要求。

3  控制仿真

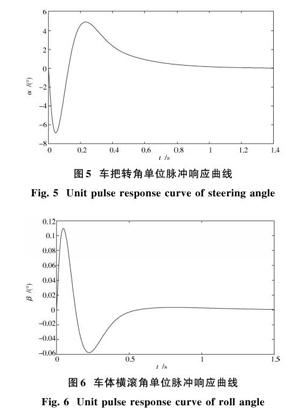
复合控制的系统特征根为-531.65，-4.284，-13.29 +0.130 3i，-13.29-0.130 3i，全部具有负实部，因此系统稳定。为验证设计的复合控制的控制效果，对系统进行仿真实验，图5和图6分别为车把转角和车体横滚角在单位脉冲扰动下的响应曲线图。由图可以看出系统在干扰的作用下，车体横滚角和车把转角都发生了震荡，但在复合控制的作用下，分别经过0.6 s和1.2 s的时间，车体横滚角和车把转角基本收敛到0。

下面分析参数摄动对系统仿真结果的影响。令系统标称状态方程式（3）中的系数发生摄动，参数摄动分为以下三种情况：式（3）的矩阵A中的16.972 2摄动到10;矩阵B中的119.623 2摄动到102;矩阵A中的16.972 2摄动到10，矩阵B中的119.623 2摄动到102。

图7和图8给出了这三种参数摄动情况下系统在本文设计的控制器下的扰动动态特性曲线。

从仿真结果可以看出，摄动前后结果变化不大，这表明设计的控制器具有很强的鲁棒性。

为了说明所设计控制器的鲁棒性，在镇定不稳定子系统的基础上，采用PD控制器在上述三种参数摄动情况下的系统动态响应曲线进行对比，如图9和图10所示。通过调整控制器的参数[KP]，[KD]，得到超调最小的PD控制器。

[KPD（s）=200（s-0.5）s+311 ] （13）

虽然PD控制器响应速度快，但是车把转角的超调非常大。在矩阵A参数摄动的情况下，车把转角已经达到了80°，极不利于自行车的平衡控制，不满足系统的性能要求。矩阵B参数摄动时，车把转角已经发散。矩阵A，B参数摄动时，车体横滚角已经发散。而本文设计的控制器使得系统具有很好的动态变化过程，在有干扰的情况下超调更小，可以抑制参数不确定对系统带来的影响，能够适应环境的变化，保证自行车机器人系统的稳定性。

4  结  语

自行车机器人作为不稳定零动态系统，既有非最小相位零点，也有不稳定极点，宜采用复合控制。本文首先对不稳定子系统设计二次型性能指标最优控制器，镇定内环不稳定子系统，系统的零动态具有不变性，外环设计一般的鲁棒控制器，使整个系统具有更强的鲁棒性。仿真结果表明，所设计的复合控制可以有效地实现自行车机器人的平衡控制，抑制参数不确定和干扰对系统带来的影响，比传统的PD控制器有更好的鲁棒性。

注：本文通讯作者为王涵。

参考文献

[1] MIYAHARA R， YAMAKITA M. Path following control of bike robot [C]// Proceedings of AETA 2017 Recent Advances in Electrical Engineering and Related Sciences： Theory and Application. Cham： Springer International Publishing， 2017： 597?606.

[2] 李雪冰，马莉，丁世宏.一类新的二阶滑模控制方法及其在倒立摆控制中的应用[J].自动化学报，2015，41（1）：193?202.

LI Xuebing， MA Li， DING Shihong. A new second?order sliding mode control and its application to inverted pendulum [J]. Acta Automatica Sinica， 2015， 41（1）： 193?202.

[3] 李德仁，李明.无人机遥感系统的研究进展与应用前景[J].武汉大学学报（信息科学版），2014，39（5）：505?513.

LI Deren， LI Ming. Research advance and application prospect of unmanned aerial vehicle remote sensing system [J]. Geomatics and Information Science of Wuhan University， 2014， 39（5）： 505?513.

[4] 刘延柱.自稳定的无人自行车[J].力学与实践，2015，37（1）：146?148.

LIU Yanzhu. Self?stable bicycle without rider [J]. Mechanics in engineering， 2015， 37（1）： 146?148.

[5] 黄用华，廖启征，魏世民，等.无机械调节器的自行车机器人圆周运动实现[J].机械工程学报，2013，49（7）：141?147.

HUANG Yonghua， LIAO Qizheng， WEI Shimin， et al. Circular motion realization of a mechanical regulator free bicycle robot [J]. Journal of mechanical engineering， 2013， 49（7）： 141?147.

[6] 叶林奇，宗群，田栢苓，等.非最小相位系统跟踪控制综述[J].控制理论与应用，2017，34（2）：141?158.

YE Linqi， ZONG Qun， TIAN Bailing， et al. Tracking control of nonminimum phase systems： an overview [J]. Control theory & applications， 2017， 34（2）： 141?158.

[7] OWCZARKOWSKI A， HORLA D. Robust LQR and LQI control with actuator failure of a 2DOF unmanned bicycle robot stabilized by an inertial wheel [J]. International journal of applied mathematics and computer science， 2016， 26（2）： 325?334.

[8] KAWAMURA T， MURAKAMI T. Robust stabilization control for an electric bicycle [J]. Electrical engineering in Japan， 2014， 188（4）： 68?77.

[9] THANH B T， PARNICHKUN M. Balancing control of bicyrobo by particle swarm optimization?based structure?specified mixed H2/H∞ control [J]. International journal of advanced robotic systems， 2008， 5（4）： 395?402.

[10] SHAFIEKHANI A， MAHJOOB M J， AKRAMINIA M. Design and implementation of an adaptive critic?based neuro?fuzzy controller on an unmanned bicycle [J]. Mechatronics， 2015， 28： 115?123.

[11] 张静，王广雄，何朕.不稳定零动态系统的鲁棒控制[J].控制理论与应用，2005，22（1）：67?71.

ZHANG Jing， WANG Guangxiong， HE Zhen. Robust control of systems with unstable zero?dynamics [J]. Control theory & applications， 2005， 22（1）： 67?71.

[12] 于秀丽，魏世民，郭磊.自行车机器人系统的稳定滑模控制[J].控制与决策，2011，26（3）：464?468.

YU Xiuli， WEI Shimin， GUO Lei. Stable sliding mode control of bicycle robot system [J]. Control and decision， 2011， 26（3）： 464?468.