基于GRA 的模糊核聚类DRVM 软测量建模与优化
黄永红,吴红生,虞永胜
(1.江苏大学 电气信息工程学院,镇江212013;2.江苏弗洛瑞生物工程设备有限公司,镇江212200)
近年来,随着现代生物技术的不断发展,动物细胞体外悬浮培养技术备受关注,已广泛应用于各类生物制品以及兽用疫苗的生产研究过程中[1]。我国是农业大国,同时也是畜牧养殖业大国,动物传染病的暴发流行对我国国民经济影响较大[2]。禽流感病毒AIV(avian influenza virus)是动物界常见的一种急性传染病,目前全世界每年约有(25~50)万人死于AIV[3]。我国现阶段预防AIV 的主要方法是采用灭活疫苗免疫接种,当前,大多数的禽流感灭活疫苗均通过禽流感疫苗细胞体外悬浮培养的方式进行病毒抗原的大量生产。该方法具有活细胞密度高、空间利用率大、工艺条件稳定等优点。
禽流感疫苗MDCK 细胞体外悬浮培养是一个高度复杂的非线性过程,培养过程包含许多难以实时在线测量的关键状态变量,如基质浓度(主要为葡萄糖)、代谢产物(主要是乳酸)和活细胞密度等。这些变量直接影响着MDCK 细胞的产量和质量,所以实现悬浮培养过程的实时在线监测和控制、优化培养条件,从而使细胞达到最佳生长状态是大量高效制备禽流感疫苗的前提[4]。
1 软测量建模技术的研究进展
软测量技术,利用易在线测量的量来预测难以实时在线测量的量,是合理解决以上弊端的主流方式。传统的软件测量建模方法,例如多元线形回归法和基于时间序列的分析法,无法获取最佳的预测结果。
人工神经网络算法在非线性计算方面优势显著,并在工业建模和模型优化方面得到普遍推广,人工神经网络结果的建立具有较强的主观性特点,且在具体学习阶段弊端显著。文献[5]采用灰色关联度分析法GRA 法建立人工神经网络系统,并对粮食产量进行科学预测,在前期对输入变量的筛选剔除主观性影响,提升了BP 网络的自适应能力和预测精度。文献[6]基于几种典型的预测模型的精度及鲁棒性特点,提出了模糊聚类分析法FCM 的多模型结构特点。
文献[7]选用最小二乘法支持向量模型,并将其应用在草酸钴粒度的测试实践中,获取了最终单一化最小二乘支持向量模型的高精度预测结果。然而,在具体的工业生产实践中,该预测模型存在一定的滞后性,例如:系统的数据存储单元在工作时存在延时性,导致数据传输出现延时,而静态软测定建模技术尚未分析滞后因素,致使变量和主变量之间的关系出现异常,最终导致建模结果精度降低。
文献[8]将动态软测量应用到BHK-21 细胞悬浮培养的活细胞密度、乳酸浓度和葡萄糖浓度的软测量上,提出了一种动态关联向量机DRVM 软测量。关联向量机RVM(relevance vector machine)具有支持向量机SVM(support vector machine)的所有优点,与SVM 相比,RVM 更稀疏、 更适用于在线检测,并且动态软测量更符合实际工业生产。然而,DRVM模型也存在一些问题,如模型的预测时间长,其泛化能力受实际生产中数据缺失等的影响严重。
综上所述,在此提出一种基于灰色关联分析和核模糊聚类的动态关联向量机GRA-KFCM-DRVM的测试建模技术。
2 DRVM 模型简介
2.1 静态RVM 建模
设给定样本集{vi,ti},其中:i=1,2,…,n;vi∈Rd,vi为输入样本;ti∈R,ti为输出采 样值;n 为样本总数。通过对样本的学习,其回归模型与SVM 相同,即
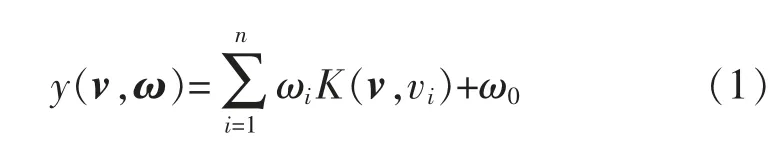
式中:{ωi}为权值向量;K(v,vi)为核函数,一般取高斯径向基RBF(radial basis function)核函数,即

假设,vi与ti都属于独立分布,且噪声εi服从均值为零方差为σ2的高斯分布,则其输出为

若目标值ti独立同分布,训练样本集的似然函数为
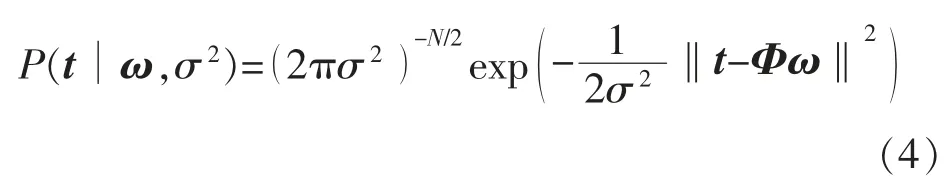
其中
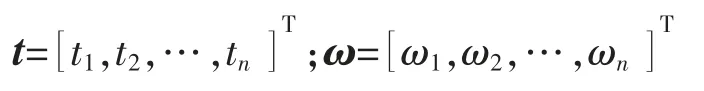
式中:Φ 为核函数组成的n×(n+1)阶矩阵,即
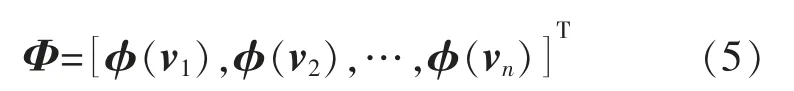
其中
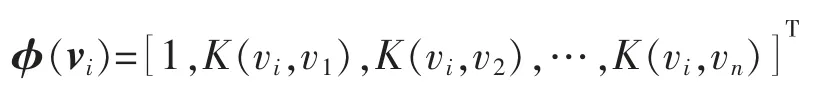
为了防止在评价ω 极大似然估计时过学习问题的出现,并进一步提高模型的泛化能力,RVM 定义的每个权值的高斯先验概率分布为
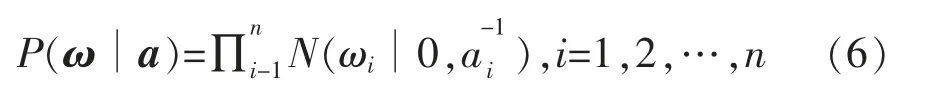
其中
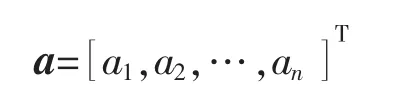
式中:a 为决定权值ω 的先验分布的超参数。
RVM 算法推理过程的流程如图1 所示。

图1 RVM 算法流程Fig.1 RVM algorithm flow chart
2.2 动态RVM 建模
通常采用{x(k),y(k)}的形式进行软测量建模,这是当前测试实践中普遍使用的静态测量建模技术。该技术采用静态测量模式,并将滞后及延时因素考虑在内。与稳态技术相比,在工业生产实践中,很多流程处于动态过程中,实际的工业测量难以保证其始终处于工作区域内。换言之,在k 值影响下的输出变量不仅是k 时刻的数据输入x(k),还包括过渡阶段的x(k-1),x(k-2),…,x(k-m+1),其中m为数据长度。考虑实际生产过程的动态因素,动态关联向量机DRVM 软测量模型的原理如图2 所示。

图2 DRVM 软测量原理Fig.2 DRVM soft sensing schematic
在图2 中经过动态加权后新的输入变量为
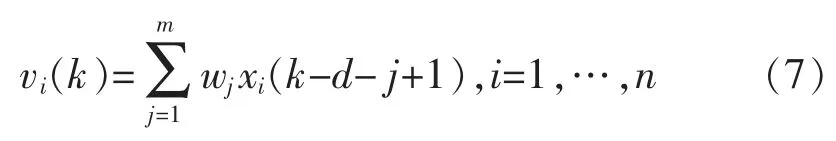
式中:n 为辅助变量的个数;m 为数据长度;d 为人为测量造成的纯时延;wj为动态权值。则DRVM 的预测输出为
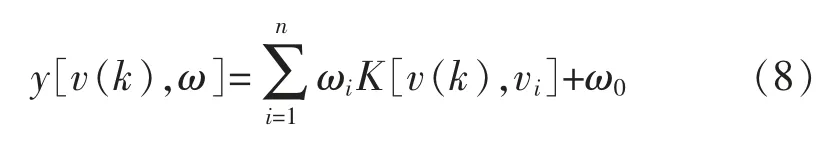
3 DRVM 模型优化
取自现场工业生产现场的样本尚未降噪,而且在生产实践中依照现场调度情况进行的生产调整,会造成很多孤立点的存在和数据的遗失,这些都会不同程度地影响动态关联条件下向量模型的数据训练效果,且DRVM 模型对于训练集合中的数据降噪要求及孤立点敏感性较高[9]。为了切实克服这一弊端,建立了满足这种不完整数据且存在噪音的模糊核聚类算法,实现输入数据的智能化遴选,降低奇异点对支持向量机的模型影响。
聚类分析是将一组已经给定的未知样本数据依照类型划分,使得相同类型样本的相似度较高,且不同类型的样本相似度低,聚类分析的目的是深度描绘数据的内在结构形式。其中,模糊c-均值聚类分析算法FCMA(fuzzy c-means algorithm)将模糊数学基本理论与聚类分析相结合,是当前主要使用的聚类分析法之一[10]。使用核函数并将其添加到FCM内,建立模糊矩阵,通过数据输入空间引导一类核函数的依赖距离测定,并将FCM 在欧拉坐标下的距离标准推广到相同空间内的不同距离聚类测量中,提升不完整数据及噪音数据的鲁棒性和精度指标。
模糊核函数距离算法的目标函数[11]为

式中:xj为样本集;vi为聚类中心;隶属度值uij应满足以下3 个条件:
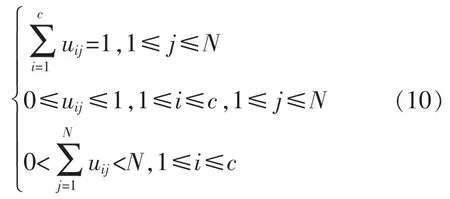
定义核函数K(x,y),满足

将式(9)展开并代入核函数,在式(10)的约束下优化,得到
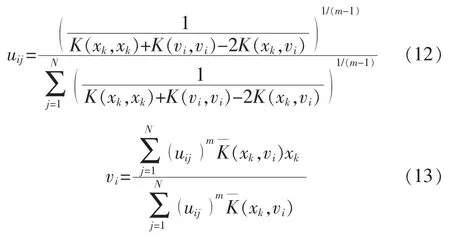
最终,把样本分成N 个子类,并对不同的子空间建立相应的关联随机向量模型,依照样本的时间、空间特点和分布情况,对不同类型的样本赋值不同的隶属度指标uj,采用加权计算法得到的输出结果为

4 GRA-KFCM-DRVM 模型的建立
4.1 软测量模型主导变量的选择
MDCK 细胞体外悬浮培养过程中营养物质的耗竭和大量代谢副产物的积累是限制活细胞生长密度、影响培养过程的主要因素,而细胞生长过程中主要的营养物质是葡萄糖,此外还有8 种必需的氨基酸及其他非必需氨基酸。
葡萄糖为MDCK 细胞生长提供主要的碳源,是最重要的能源来源之一,葡萄糖通过分解产生乳酸。分析葡萄糖的浓度值和乳酸浓度值的高低,对MDCK 细胞体外悬浮培养生产禽流感疫苗的过程影响显著。此外,活细胞的浓度指标是禽流感疫苗生产效率的重要表征,参数值预测的目的是为了能够更加精准地测定并控制活细胞的浓度,为生产疫苗做储备。故在此选定葡萄糖浓度、乳酸浓度、活细胞浓度作为DRVM 测量模型的主变量。
4.2 软测量模型辅助变量的选择
影响DRVM 模型主导变量的因素有很多。所选择的输入变量过多会加大模型的复杂度,增加模型预测时间;选择不当还会影响模型预测精度。
灰色关联分析(GRA)属于一类相对性的序列排布分析法[12]。它可以测定系统内不同因素的关联度,进而为确定细胞浓度等因素的重要性奠定基础。GRA 理论的核心思想是基于空间结合图形外形相似度的关联度评价[13]。其计算流程如下:
步骤1计算表征行为特点的输出序列及影响行为系统的输入序列的标准化处理方式。
步骤2关联度的计算。在t=n 时,输入序列{xi(n)}和输出序列{xo(n)}的关联指标为
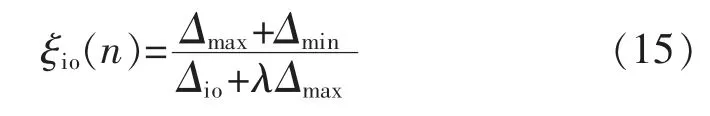
式中:λ 为分辨系数,且0<λ<1;Δmin为第二最小差值;Δmax为两级的最大差值;Δio(n)为不同输入序列的{xi(n)}曲线对应的输出序列{xo(n)}中的不同点的差值绝对值。
步骤3关联度τio的计算。输入及输出序列的关联度标准计算为

步骤4关联度的序列排布。计算关联度指标的序列值。采用灰色关联度计算法,定量分析不同因素对测试软件及模型的影响程度[14]。从原理层面分析,得到影响主导变量的环境变量有:温度T(X1),pH 值(X2),O2溶解量DO(X3),O2分压PO2(X4),CO2分压PCO2(X5),体积V(X6),压力P(X7)。进一步对所得变量做灰色关联分析,计算出每个变量与主导变量葡萄糖浓度(Y1)、乳酸浓度(Y2)、活细胞密度(Y3)的关联度; 选择1 个培养批次的数据作为样本,取分辨系数λ=0.5,计算结果见表1。

表1 环境变量与主导变量的关联度Tab.1 Relevance between environmental variables and dominant variables
根据表1 关联度指标计算结果,分析不同环节的变量之间的相互关联度指标,然后按照综合关联度的大小进行排序,得到:A2>A6>A3>A1>A4>A5>A7(其中A 为各环境变量与主导变量的综合关联度)。此外,PO2,PCO2及P 与主导变量的关联度均低于0.5,表明这3 个变量对主导变量的影响不大。因此最终选择T,pH,DO,V 这4 个环境变量作为辅助变量。软测量模型结构如图3 所示。

图3 DRVM 软测量模型结构Fig.3 DRVM soft sensing model structure
4.3 GRA-KFCM-DRVM 软测量建模
试验中共采集5 个培养批次的数据,对样本数据进行归一化处理分析,并将归一化后的数据(不同批次数据含有58 个样本,不同样本中含有7 个变量,分别为软测试变量模型的辅助变量和主体变量)拆分为2 批次,一批次为训练样本,用于训练人工神经网络(前4 批次,含232 样本),另一批次为测试样本集合(另5 个批次,58 个样本)。
根据样本的数据特点,把232 个样本分为16类,并对不同的子类型建立动态化的关联向量机模型,依照样本在时空上的分布特点,对不同的样本赋值不同的隶属度指标ui,借助加权计算法得到输出结果。软测试建模分析流程如图4 所示。

图4 基于GRA-KFCM-DRVM 软测量建模Fig.4 Soft sensing modeling based on GRA-KFCM-DRVM
5 GRA-KFCM-DRVM 模型验证
基于MDCK 细胞悬浮培养生产禽流感疫苗阶段的技术要求,将反应器内的温度保持在36.5 ℃左右,pH 值控制在7.0~7.2,匀速搅拌速率控制在30 r/min,氧气溶解量控制在40%~45%。
为验证GRA-KFCM-DRVM 模型的预测精度,将其与DRVM 软测量模型预测结果做对比。在MatLab 环境下进行仿真,仿真结果如图5,图6 和图7 所示;误差如图8,图9 和图10 所示。
由图5,图6 和图7 可见,与DRVM 模型的预测效果相比,GRA-KFCM-DRVM 模型的预测结果更接近参数的真实值,同时GRA-KFCM-DRVM 的确定系数R2更接近于1。说明GRA-KFCM-DRVM 的预测精度较高于DRVM。

图5 葡萄糖浓度预测趋势曲线Fig.5 Trend curve for predicting glucose concentration

图6 乳酸浓度预测趋势曲线Fig.6 Predictive trend curve of lactic acid concentration
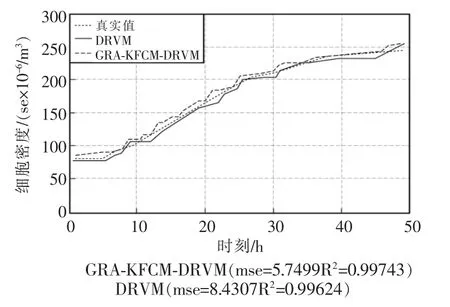
图7 活细胞密度预测趋势曲线Fig.7 Trend curve for predicting living cell density
葡萄糖浓度预测误差曲线如图8 所示。由图可见,DRVM 模型的最大误差为7.7%;GRA-KFCMDRVM 模型的最大误差为3.6%。结果表明,GRAKFCM-DRVM 模型的预测精度更高; 由图形的走势可见,GRA-KFCM-DRVM 波动更小、更加稳定。
乳酸浓度预测误差曲线如图9 所示。由图可见,DRVM 模型的最大误差为6.6%;GRA-KFCMDRVM 模型的最大误差为4.9%,小于DRVM 模型的预测误差,且随着样本量的增加GRA-KFCMDRVM 模型的预测误差越来越稳定。DRVM 模型和GRA-KFCM-DRVM 模型的活细胞密度预测误差曲线如图10 所示。由2 个模型的走势可见,GRA-KFCM-DRVM 模型的预测精度更高且更稳定。

图8 葡萄糖浓度预测误差Fig.8 Prediction error of glucose concentration

图9 乳酸浓度预测误差曲线Fig.9 Error curve of lactic acid concentration prediction

图10 活细胞密度预测误差Fig.10 Prediction error of living cell density
为了更直观地说明GRA-KFCM-DRVM 模型的优势,利用最大误差eMSE,决定系数R2和预测时间3个性能评价指标来反映其优越性(见表2)。由表可知,GRA-KFCM-DRVM 模型的误差更低,R2更接近1;DRVM 模型的预测时间更短,但与GRA-KFCMDRVM 模型相差不大,且GRA-KFCM-DRVM 模型的预测时间在合理的范围内。结果表明GRAKFCM-DRVM 模型性能更好。

表2 模型的性能比较Tab.2 Performance comparison of model
6 结语
在动态关联向量机的基础上,提出基于灰色关联分析的模糊核聚类DRVM 软测试建模技术,并对通过灰色关联度遴选的样本进行模糊核聚类分析,降低或者直接剔除缺失数据和噪音数据对动态关联向量机模型的影响程度。选用真实数据的论证结果表明,基于静态软测试模型基础而建立的动态软测量模型,相较于一般静态模型,能够深刻反映工业生产阶段的动态化本质特点;通过灰色关联分析确定了与主导变量密切关联的辅助变量,减少了计算维度,利用模糊核聚类对新样本进行聚类,增强了模型鲁棒性,提高了模型的泛化能力;通过仿真验证分析,与原有的DRVM 模型相比,GRA-KFCMDRVM 模型的预测精度更高、更稳定。

