结合视觉显著性的多聚焦图像融合算法
赵 欣,曹 敏
(武汉工程大学 电气信息学院 智能与车联网实验室,武汉430205)
图像融合是图像处理中的重要部分,是将不同方式或者不同传感器下获得的多幅图像融合成为一幅图像,使图像能更加适合于人类视觉感知,或能便于在计算机上进一步处理与分析的融合图像的处理方法。多聚焦图片融合在图像融合中十分重要,是在场景中对不同目标物分别进行聚焦成像,得到有关该场景目标物的多幅多聚焦图像,然后采用某种算法提取各自的清晰区域,并将这些区域合并生成一幅该场景中所有景物都清晰的图像。当前,图像融合技术已经在军事、数码相机等方面应用广泛[1]。
1 理论分析
1.1 频率调谐FT 显著性检测
显著性物体检测模型侧重于将图像中受到视觉注意的物体完整地提取出来,其中以频率调谐FT(frequency-tuned)模型的应用最为广泛。FT 显著性检测算法由Achanta 等[2]人提出,使用FT 模型计算得到的显著图与原图像分辨率一致。在此引入FT算法以提取多聚焦图像的视觉显着图。
在FT 方法中,高斯差DoG(difference of Guassian)滤波器的差异基于高斯滤波器函数的空间分布,作为带通滤波提取频域中的显著性。首先对输入图像采用高斯差分对图像进行滤波。高斯差分公式为

设置高斯方差比例为1∶1.6,能够更好地检测物体的边缘。组合多个DoG,即将所有的高斯差分结合在一起,就可以从不同的尺度空间中检测图像边缘,从而检测出图像中的显著性区域。对多聚焦图像高斯滤波得到滤波后的图像,计算显著值得到显著图。像素的显著性计算公式为
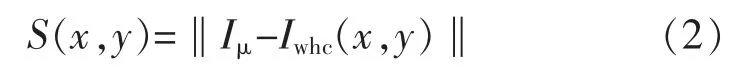
式中:Iwhc(x,y)为像素点的Lab 值;Iμ为图像在Lab空间的均值。
1.2 非下采样轮廓波变换NSCT
随着在Contourlet 变换的广泛应用,2005 年A.L.Cunha 等在轮廓波的基础上提出了非下采样轮廓波变换NSCT(non-undersampled contour wave transform)算法[3]。NSCT 不仅保有多尺度、局部特性和多方向性,还增加了平移不变性和更高的冗余度;由非下采样金字塔NSP(nonsubsampled pyramid)和非下采样方向滤波器组NSDFB(nonsubsampled directional filter bank)2 个部分组成[4]。
非下采样金字塔分级结构经多级迭代方式完成,由一组低通和高通滤波器组组成[5]。非下采样滤波器组的结构分为2 部分,一部分用扇形滤波器组和象限滤波器组将图像分为4 个方向子带,另一部分利用平行滤波器组迭代出不同方向的子带。
NSCT 处理图像时,如图1 所示,首先采用非下采样金字塔滤波器组NSPFB 对图片进行多尺度的分解,获得低频子带和高频子带,自由设定所需要分解出的层数,将有不同的高频子带出现; 再用NSDFB 对图片进行高频子带分解,即可得到各尺度和方向的子带系数。

图1 NSCT 分解框架Fig.1 NSCT decomposition framework
1.3 本文算法
在此将非下采样轮廓波变换与视觉显著性相结合对融合规则进行了改进,实现不同聚焦源的图像融合。假设,A 和B 为输入的2 幅聚焦源不同的多聚焦图像,F 为最终的融合图像。本文算法的图像融合流程如图2 所示。

图2 本文算法的图像融合流程Fig.2 Flow chart of image fusion based on this algorithm
2 融合规则
融合规则作为图像融合算法的关键之一,其对图像的融合效果有非常大的影响。多聚焦图片A 和B,经过NSCT 分解后,分为低频子带系数和高频子带,其各自包含的物理信息有着明显的差异: 低频子带主要包含图像的相似部分,即图像的背景信息;高频子带则表征图像的轮廓纹理细节部分。在此将针对低频、高频子带各自的特点制定融合规则。
2.1 高频系数融合规则
一般高通子带系数反映了图像边缘或细节等。多聚焦图像的像素值变化剧烈的点一般是聚焦区域内的点,因此高频子带图像常使用系数绝对值取最大的融合准则,然而使用其融合图像中的细节容易产生间断。为了缓解这样的情况,对于高频系数的融合规则,将采用拉普拉斯能量和比较的方法[6]。拉普拉斯能量和能更好地表征图像的边沿特征信息,反映图像的聚焦特性和清晰度。拉普拉斯能量和的数学表达为
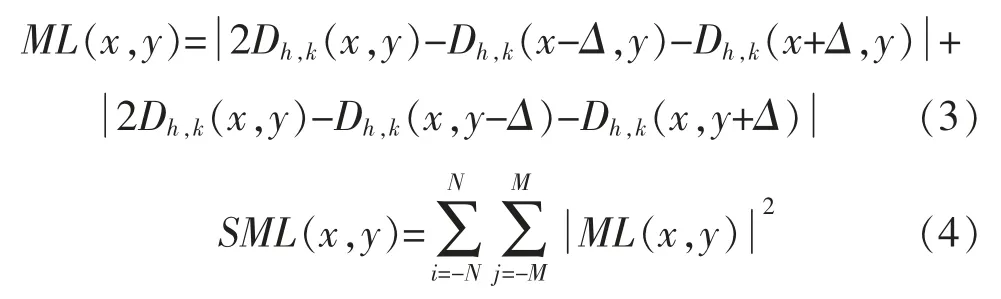
式中:SML(x,y)为图像中该点像素的清晰度信息。
比较高频子带拉普拉斯能量和[5],确定高频子带系数为
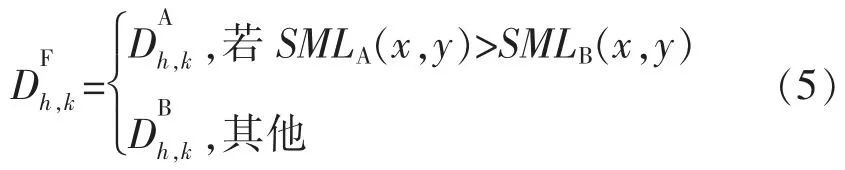
2.2 低频系数融合规则
低频子带系数表征了源图像的背景信息,其融合效果对图像轮廓有着决定性作用,并且影响着图像的对比度[7]。低频系数一般表示源图像的近似分量,使用FT 算法检测,背景会具有更高的显著值。对显著、非显著性的区域分别采用以下相应融合规则:
——在显著性区域采用自适应权重融合规则。


——非显著性区域采用基于区域能量RE(regional energy)的融合规则。

3 试验结果分析
为了验证所提出的结合显著性方法在多聚焦图像融合的可行性,对3 组多聚焦图像进行了融合试验。将本文算法与NSCT 方法、SR[8]方法、NSCT 结合SR[8]的方法分别进行对比。图3 和图4 分别为时钟、花、草图像组的试验结果。其中,每组的源图像A为左聚焦图像,源图像B 为右聚焦图像。
在此,使用互信息MI(mutual information),边缘信息保持量Qabf,Piella 评价指标(Q0,Qw,Qe),结构相似度SSIM(structural similarity)和图像清晰度FD(fusion definition)共7 项客观评价指标,以评价各融合图像的性能[9]。试验中,图片融合效果越好,相应的评价指标的值应越高。

图3 多聚焦源图像Fig.3 Multi-focus source images

图4 各种融合方法的试验结果Fig.4 Different fusion methods of experimental results
通过图4 和表1 可见,本文算法的试验结果评价指标中的Qe,Q0和FD 值都是最大的,说明其融合图像在清晰度上优于其他方法;本文算法的时钟和花2 组指标MI 的值比之其他方法更高,而草的MI 指标为第2 大,也说明在本文算法融合后的图像获得了源图像较多的信息量;Qabf和SSIM 也取得了较好的结果,说明通过本文算法融合后的图像留取了原图更多的边缘信息,并能较好地保留原图的结构信息。

表1 图像融合的客观评价效果指标Tab.1 Objective evaluation of fusion results
4 结语
针对多聚焦图象的特点,为了使最终的融合图像包含更多的细节信息如纹理边缘等,基于NSCT变换的多种良好特性,提出了通过结合显著性的改进的多聚焦图像融合算法。由试验结果可以看出,本文算法较好地保留了源图像的边缘、细节和纹理等,在一定程度上提高了多焦点融合图像的对比度和清晰度; 与以前的算法相比,融合效果得到了改善。

