阅读引领人生 智慧点亮课堂——记邯郸市涉县新北关小学教师申武广

课堂教学

奇妙的“剩余”——《正方形和圆之间部分的面积》教学实例

【课前思考】

《正方形和圆之间部分的面积》一课是在学生学习了圆的认识、周长和面积以及圆环的面积之后进行教学的，是人教版六年级教材新增加的教学内容。编排目的是通过解决圆的内接正方形、外切正方形与圆之间部分的面积这一实际问题，让学生经历问题解决的全过程，并在解决具体问题的基础上发现更为一般的数学规律。在实际教学中，如果仅仅将本课作为“记忆规律、熟练应用”的教学内容，就会违背教材编写的初衷。作为典型的“问题解决”类例题，如何让本课上得更加丰满和深刻呢？某次笔者随意翻看例2和例3时，突然有了自己的“发现”：两个例题都是对剩余部分的求解。剩余，很有意思吗？我们以前解决问题时是否有过求“剩余”的经历，将来在学习中会不会遇到“剩余”类问题呢？笔者通过查阅资料和研究教材，对“剩余”进行了适度拓展和深度挖掘。

【教学流程】

1.激发兴趣，开拓思路。课伊始，教师单刀直入，亮出课题，让学生谈谈对“奇妙的剩余”的看法，学生顿时兴趣盎然。然后出示三道“剩余”类问题：（1）申老师本月工资3825元，到月底消费了2000元，还余下多少元？（2）直角三角形的一个锐角是40°，另一个锐角是多少度？（3）一项工程，已完成，还剩下几分之几？学生计算思考。本环节旨在初步感知“剩余”类问题，从“剩余”切入，打开思路，引入本课主题。

2.逐步深入，聚焦问题。教师课件呈现几个学过的平面图形，随机选择正方形来研究。然后出示两个大小不同的正方形，学生指出把两个正方形组合在一起，就会出现“剩余”问题：大正方形和小正方形之间的部分面积是多少？老师抛出问题：给你几个数据，就能求出这个问题。接下来，课件将小正方形旋转，进而产生新的“剩余”问题，从而激发学生浓厚的探究兴趣。有学生说只要知道大正方形的边长就能求出剩余面积，中间小正方形的面积分割为两个三角形求出，这样就为后面圆与正方形的研究奠定了基础。在此基础上，课件继续出示圆形，两个大小不同的圆即可产生“剩余”问题，学生惊讶：这不就是刚学过的圆环吗？除了正方形和圆形各自能够发现“剩余”问题，那么正方形和圆形之间能不能发生碰撞呢？学生很快想到圆内接正方形和圆外切正方形两种情况，通过自主探究和小组合作，仅仅利用圆的半径一个条件就将剩余面积问题全部解决，也就解决了本课的主要问题，得出结论：如果两个圆的半径都是r，那么外方内圆之间部分的面积是0.86r2，外圆内方之间部分的面积是1.14r2；不仅如此，更重要的是学生积极主动地参与了发现、提出、分析和解决问题的全过程。

3.拓展延伸，感悟“剩余”。

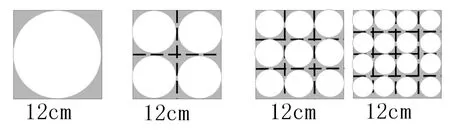
（1）课件出示：三张边长都是12厘米的正方形铁皮，分别按下图不同规格的图片剪裁，哪张铁皮剩下的废料多？（解决完前三个图形之后，然后猜测第四个图形会不会剩下废料最多）

（2）看下面的图形，关注它的剩余部分，你发现了什么？（课件逐步展示）

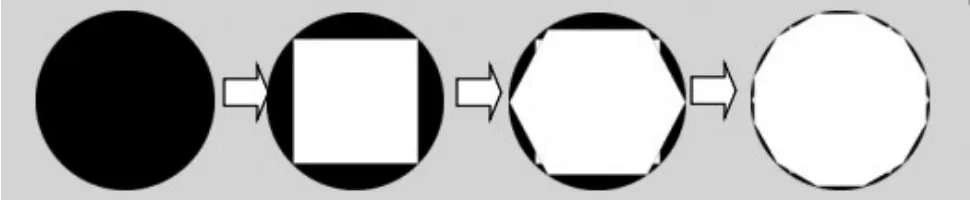
学生发现，剩余部分的面积越来越小，直至为0。老师课件出示：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体，而无所失矣。”这句话是我国古代数学家刘徽说的，他就是利用这样分割的办法来研究圆的周长和面积的，被称为“割圆术”。割圆术，则是以“圆内接正多边形的面积”，来无限逼近“圆面积”。学生看罢大为惊叹！接下来，教师呈现生活中“剩余”部分的应用。两道拓展题，将“剩余”类问题向深度和广度推进，学生的问题意识愈加增强。这样的“剩余”，变中有变，变中亦有不变，真可谓奇妙无穷！

4.提出问题，走向课外。关于“剩余”，你还想研究哪些图形之间的关系？学生踊跃发言，有的说三角形与圆形，有的说长方形与圆形……通过本课的研究将问题引向课外，对于学生数学兴趣和问题探究能力的培养都具有极其重要的作用。从整堂课看来，“剩余”问题表面简单，但细究下去、生发开来，却形成一个便于学生不断发现和提出问题的问题场，无论课始还是课尾，学生都在这样的探究环境中积极主动地思考着，分析和解决问题的能力也在逐渐增强。

亦教亦思

创设“好吃又有营养”的数学课堂

○申武广

作为一名专业的小学数学教师，都会时不时地对小学数学课堂进行本质性追问：儿童需要学习什么样的数学？儿童喜欢以什么样的方式学习数学？通过学习数学，儿童到底应该从中获取什么？为此，全国著名小学数学特级教师吴正宪老师提出了“好吃又有营养”的数学课堂。正是吴老师的这个观点深深影响着我、激励着我、引领着我。

1.阅读引领，提升理论水平。当你对教材上的知识点迷惑不解时，当你对课堂中学生出现的问题无法处理时，当你对当下小学数学教育的某些改革困惑不已时，你会怎么做？我会毫不犹豫地选择阅读。在阅读中，吴正宪老师的课堂深深吸引了我，一句话：好吃又有营养！好吃，是从学生的角度来说的，课堂只有学生喜欢才会认真地听，只有喜欢才会主动思考，所以教师必须了解学生。营养，是从数学的角度来说的，课堂表面热闹，如果没有“数学味”，就不是一节真正的数学课，所以教师必须理解数学。《奇妙的“剩余”》一课，不仅大大激发了学生对数学问题的探究兴趣，而且提出许多有价值的问题，然后通过学生独立思考、小组讨论、集体交流，经历了一次如同数学家研究问题的思考过程。也可以说，本节课是我长期以来不断阅读积累，努力创设“好吃又有营养”的数学课堂的一次成功尝试。

2.反思跟进，成就梦想课堂。坦诚地说，这节课在不同的班级共上了三次。第一次，按教材编排教，学生跟着老师的思路解决问题，遇到困难处教师点拨。固定的方法，明确的思路，学生收获很有限。第二次，对教材增加难度，让学生总结出两种情况的面积求解公式，并且练习上也进行了拓展。学生的探究兴趣依然不高，公式总结不过如此。到底哪里出了问题？两次失败让我痛定思痛，本课的探究性比较强，如果按一般的课堂流程来教，势必难以激发学生的思考欲望。闲暇之余，读到了张景中院士的一篇文章《好的老师应当向学生展示数学思维的美妙》，联想到我的课堂，为什么不“好吃”呢？就是因为没有展现出探究数学问题的乐趣。接下来，我对教材内容进行了整合改编。学生先从正方形开始思考，两个正方形即可产生“剩余”，将小正方形旋转产生的“剩余”更有趣；然后从圆形开始，两个圆形形成的“剩余”正好是圆环，让学生意想不到，加深了对“剩余”的认识；接着正方形和圆形两个图形组合变换形成“剩余”问题，产生了这节课重点研究的内容：圆中方、方中圆。最后在圆内接图形中“剩余”部分的越来越小，竟然与著名的“割圆术”有关，由此给学生留下了难以忘却的印象。许多学生在课后不禁感叹：数学中的“剩余”问题真的好奇妙呀！

我想，这才是一节“好吃又有营养”的课吧！

像这样的反思，我从未停止过。每节课上完之后，都要把学生的课堂表现和教学的得失之处进行整理、反思、总结，并且记录下来。不论课前、课中，还是课后，我都要进行思考。由于不断反思课堂教学，本人在国家级、省级教育类杂志上发表文章40余篇，其中《读懂教材：有效教学的基本保障》获中国教育学会小学数学专业委员会第十五届论文三等奖，并参与编写了小学生优秀读物《数学在哪里》，在河北省十佳期刊《小学生必读》连载数学故事20多篇，深受孩子们的喜爱。

名师点评

精彩源于思考——我眼中的申武广老师

○李书朝

多次听申武广老师的数学课，印象最深的就是他爱思考，爱琢磨，课前慎思，课后反思。他一直坚持，从未间断这种优秀的思考习惯。正因为如此，在别人认为很平常的课，经他一设计，总能见到精彩之处。他的上课风格和特点，从《奇妙的剩余》一课，可以略见一斑。

1.课因“思”而“易”。“外圆内方”和“内圆外方”问题，在多数教师的眼中是比较难教和难学的内容。如何化难为易，使之便于学生理解和接受？申老师站在课程的高度，从数学的本质入手，对教材进行了大胆地重组和建构，较好地突破了这一难点。三角形度数问题、收支问题、工程问题与组合图形问题在我们看来关系不大，但在申老师眼里，它们都是剩余问题，基本算法都是“减法”，而“剩余”就是这些问题的共性和本质。基于这种考虑，本节课紧紧抓住“剩余”这一主线，将看似无关却又内在紧密的问题联系起来，大大降低了学生的思维难度，使数学变得好学起来，从而给每个学生提供了平等学习的机会。

2.课因“思”而“深”。深刻而丰满是申老师数学课的又一特点，他的课总能够把着眼点和落脚点放在经历、体验与知识的自主建构上，引领学生在积极探究和思考的同时深入体会所蕴含的数学思想。本节课中申老师让学生分别把大小两个正方形、两个圆、正方形和圆进行组合，在创造“剩余”的过程中理解这类问题的本质，体验“变与不变”的数学思想。在启发学生找出大小两个图形之间的关系，并根据关系找出条件的过程中，找到解决问题的关键。正是在这一系列的数学活动中培养了学生发现问题、分析问题、解决问题的能力，提升了学生的数学素养。

3.课因“思”而“趣”。如何让数学课堂变得“好玩”“有趣”，在“有营养”的同时“好吃”起来？是申老师一直思考和追求的目标。在本课拓展延伸环节，教师出示边长都是12厘米的正方形铁皮，分别减去1个圆、4个圆、9个圆，求哪张剩下的废料多的问题，让学生通过猜测—猜错—纠错—发现规律—推广规律（减去16个圆）等活动，充分感受数学之美，数学之趣！特别是数学史的拓展，让学生发现圆内接图形中“剩余”部分越来越小，竟然与著名的刘徽“割圆术”有关，在感受数学之趣同时受到了良好的情感态度价值观教育。

总之，申老师的课简约而不失深刻、朴实而不乏灵动，处处闪烁着智慧的光芒。学生喜欢他的课，老师欣赏他的课，专家肯定他的课，这也许就是“思考”的力量。每一节课下来，申老师总要认真反思一下，这节课上得怎么样？教学中出现了什么意想不到的问题……一旦有了什么想法，他就写到“教学反思”本上。久而久之，所思所想就逐渐多起来，对教材挖掘得更深，对学生也了解得更多了。曾记得有次申老师讲公开课，偶然间翻看了他的教学设计，在纸的空白处写满了密密麻麻的修改建议和思考心得，不禁让人佩服。由此看出，反思铸就了教学上常改常新、精彩不断的申老师。