高速列车头型近场与远场噪声预测

高 阳， 李启良， 陈 羽， 王毅刚， 钱 堃

(1. 大连交通大学 交通运输工程学院,辽宁 大连 116028; 2. 中车长春轨道客车股份有限公司 国家轨道客车工程研发中心，吉林 长春 130062；3. 同济大学 上海地面交通工具风洞中心,上海 201804)

我国高速列车技术发展不仅在国内展现其应用优势和未来潜在的应用前景，而且“走出去”已迈开了坚实的脚步，并展现出了引领国际高速列车发展趋势.高速列车高速运行带来了强的气动噪声，对车内乘坐舒适性和车外环境产生强的噪声干扰，有必要将气动噪声作为重要的性能指标.

头型具有辨识度强、结构复杂的特点，是高速列车主要噪声源.国外使用声反射镜和阵列识别出高速列车气动噪声源.Nagakura[1]在距列车25 m外使用声反射镜测量了时速300 km·h-1的新干线各部位噪声发现，头型转向架和排障器区域噪声大于其他区域，量级分别可达73 dB和76 dB.Noh等[2]开发了144通道麦克风阵列并对高速列车的噪声源进行识别，获得时速390 km·h-1高速列车的噪声分布图，确定头型转向架为高速列车的主要噪声源.

当前，高速列车车身区域湍流脉动压力等非定常流场通常使用大涡模拟和涡分离模型得到，远场噪声则通过基于声类比[3-4]的FW-H方程[5]获得.刘加利等[6]利用大涡模拟和声类比理论分别计算车头湍流脉动压力和远场噪声指出，湍流运动剧烈的头部是主要气动噪声源，其湍流脉动压力具有宽频特性，能量集中在低频段.远场噪声也具有宽频特性，且能量集中在1 800～2 800 Hz.朱剑月等[7]基于延迟分离涡模型和FW-H方程分别得到头车转向架部位非定常流场和远场噪声，指出转向架与转向架舱部位涡脱落和流体分离显著，涡结构发展较为集中.可穿透积分面方法能够有效进行高速列车远场噪声预测.作者等[8]基于大涡模拟和FW-H方程，并采用子域法实现了全尺寸高速列车头型表面湍流脉动压力和远场噪声预测.

湍流脉动压力和近场声压是车内结构噪声计算所必须的外部输入.传统基于声类比法由于将声源看作紧致源，只能计算距离声源较远位置的测点声压.为了获得近场声压，Ewert等[9]在2003年推导出了一系列声扰动方程(acoustic perturbation equations, APE)来模拟时间和空间域中由流动诱导的声场.在剪切流、旋转涡流和圆柱绕流等问题上明确了声扰动方程的优越性.司海青等[10]在声扰动方程基础上加入了一种声源项，弥补了压力峰值较小的不足.Faβmann等[11]将声扰动方程的涡量项移到右侧来改进线性欧拉方程从而形成线性扰动方程，首次在NACA0012机翼后缘上预测到多孔介质的降噪效果.

尽管声扰动方程在较早时间里被提出并被进一步发展到能够考虑多孔介质效应，但都是应用于简单流动发声问题，尚未有高速列车上的应用.目前文献大多关注车身附近湍流脉动压力和远场噪声，未考虑近场声压.由于湍流脉动压力和近场声压都是车内噪声预测的外部激励，缺一不可，因此需要尝试通过声扰动方程等手段来获得近场声压.为此，本文以某头型为对象，探索建立基于FW-H方程和声扰动方程的远场和近场噪声计算方法，结合大涡模拟得到湍流脉动压力，从而建立一整套高速列车头型气动噪声预测方法.

1 研究方法

1.1 风洞试验方法

受风洞大小的限制，目前国内外通常只能进行1∶8或更小缩比的风洞试验.为了验证数值仿真方法，选取了某头型在同济大学气动-声学整车风洞进行1∶8缩比三车编组的气动噪声试验.试验模型安装在试验段的支撑地板上.采用翼型支撑柱减少支撑柱对流动和噪声的影响，如图1a所示.模型安装到位后，对模型的姿态角进行标定，确保试验模型姿态角准确.

车外的声场环境是评估高速列车噪声的主要指标之一，为此在试验模型右侧布置3个远场麦克风.考虑到风洞结构和缩比模型气动噪声试验无法参照ISO3095标准，结合汽车通过噪声标准确定远场麦克风距车身中心截面7.5 m，高度距地板0.8 m.测点3正对中间车与尾车的车间连接处，各测点P1,P2和P3相距3.0 m，如图1b所示.

试验模型和声学测量设备安装完成后，采用声学校准器校准所有麦克风，并使用激光器确保模型处于0°.当试验风速稳定在250 km·h-1时，设定采样频率和采样时间分别为48 kHz和10 s，由动态数据采集系统进行数据采集.采集到时域信号并通过快速傅里叶变化得到测点声压级频谱和总声压级.

a 1∶8缩比三车编组试验模型

b 远场测点图1 试验模型与远场测点Fig.1 Test model and far field test points

1.2 数值仿真方法

1.2.1模型与网格

建立与风洞试验一致的高速列车数值仿真模型，模型包括车体、转向架、风挡等部件.高速列车位于图2a所示的计算域中.高速列车和计算域的长、宽和高分别约为10.2 m×0.4 m×0.5 m，18.7 m×5.5 m×2.5 m.进口距头车鼻锥约2.5 m，出口距尾车鼻锥约5.7 m.该距离约为13倍车体断面当量直径，能够最大限度减少出口扰动对计算的影响.设定与风洞试验相同的速度和湍流度，即250 km·h-1和0.2%.

依次对1∶8缩比三车编组进行面网格划分.头型曲线段的鼻锥、排障器、转向架舱、车窗和车体的面网格大小分别为2.0 mm、3.0 mm、4.0 mm、4.0 mm和5.0 mm.拖车转向架和动力转向架的面网格大小分别为2.0 mm和3.0 mm.保留车厢连接部位风挡的具体结构，采用3.0 mm的面网格.直流段面网格为5.0 mm.创建长、宽和高分别约为11.80 m×0.84 m×0.77 m的积分面，用于接收列车、地面等部件产生的偶极子噪声和四极子噪声.积分面网格为6.0 mm.

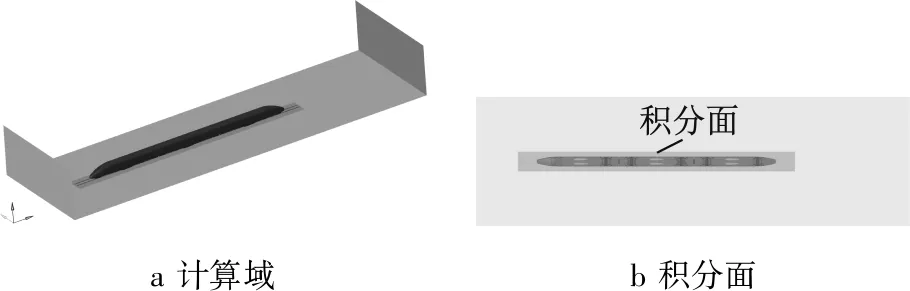
a 计算域b 积分面

图2计算域与积分面

Fig.2Computationaldomainandpermeablesurface

使用STAR-CCM+的Trimmer+layer策略生成计算域的体网格.基于大涡模拟对近壁区网格要求，生成了总厚度为0.8 mm，增长率为1.2，共计8层的边界层网格，满足第1层网格对应y+≈1.分别对头车鼻锥和曲线部位进行网格加密，加密区域如图3a所示.加密区空间网格大小分别为6.0 mm和3.0 mm.除加密区外，积分面内空间网格大小为12.0 mm.如此密的网格就是为了能使积分面内噪声可以有效传播到积分面上，从而提高远场噪声预测精度.整个计算域共生成约4 043万个体网格，满足网格质量要求，如图3b所示.

1.2.2流场计算方法

考虑到计算速度对应马赫数Ma≈0.2，不可压计算能够节省计算资源和更好收敛，因此在非定常流场计算时，采用不可压大涡模拟并结合壁面适应局部涡黏模型(wall-adapting local eddy-viscosity, WALE)[12].相比其他亚格子模型，该模型对模型系数不敏感，能自动给出准确的壁面数值，是近年使用较多的湍流模型之一.通过该模型可以得到高速列车头型湍流脉动压力特性.

a 加密区b 网格截面

图3加密区与网格截面

Fig.3Encryptedareaandgridsection

1.2.3声场计算方法

高速列车关注近场和远场噪声.近场噪声将通过车身结构进入车内，影响车内乘坐舒适性.远场噪声将影响车外声环境.

远场噪声的求解，目前应用最多的是能够考虑声源运动和固壁的FW-H方程.方程的左边为声传播项，右边依次为四极子源项、偶极子源项和单极子源项，见式1.

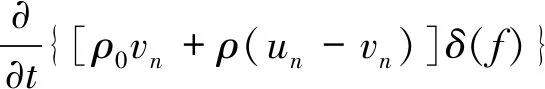
(1)

式中：α0表示声速, m·s-1；P’表示声压, Pa；Tij表示Lighthill应力张量；Pij表示压缩应力张量；ui表示xi方向的流体速度分量, m·s-1；un表示声源面的法向流体速度分量, m·s-1；vi表示xi方向的表面速度分量，m·s-1；vn表示声源面的法向表面速度分量, m·s-1；δ(f)表示迪拉克函数；H(f)表示海维赛德函数.

近场噪声需通过额外的声波方程进行求解，如声扰动方程，见式2.声扰动方程左边为声压在时间和空间的传播项，右边为声源在时间和空间的变化项.由于声扰动方程采用时域求解方式，未有过多假设，因而能够考虑声音多普勒效应、壁面反射和介质折射等声学特性，获得准确的声压.声扰动方程已在剪切流、旋转涡流和圆柱绕流等问题上有所应用.

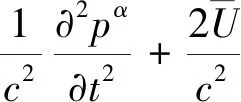
(2)

1.2.4计算设置

在仿真计算时，大涡模拟方程和声扰动方程将在整个计算域内进行计算求解.当所设定声源权重为1和声传播阻尼为0时，声扰动方程将在此区域按声源进行计算.当所设定声源权重为0和声传播阻尼为1时，声扰动方程将在该区域进行声传播计算.在源和传播计算区域中存在过渡界面，为了避免信号跳跃，就在过渡界面设置一定厚度并进行加窗处理.由于本文重点关注头型区域声压且声源计算需要密的网格，为此设定图4所示区域为声扰动区.声源区和声传播区之间采用厚度为15 mm的空间汉宁窗进行处理.

图4 声扰动区域Fig.4 Acoustic perturbation region

计算采用STAR-CCM+的分离流求解器.流动计算的时间离散格式为二阶隐式，空间离散格式为混合中间差分.噪声计算的时间离散和空间离散均为二阶.考虑空气流动对声传播带来的影响.

首先采用SST K-Omega模型[13]计算定常流场，作为非定常流场的初始条件，这样可以加速非定常流场计算的收敛.在非定常流场计算中，首先采用0.000 5 s的时间步长，一共计算0.5 s的物理时间，相当于来流流过了3倍的车身长度.足够长的物理时间能够保证流场达到动态平衡.之后，将时间步长切换0.000 05 s，并经过1 000步计算使流场的波动完全稳定，开始对平均压力和平均速度进行采样，用于后续声扰动方程的计算.经过500步的采样，平均场基本收敛，于是开始声扰动方程的计算.再经过500步后，开始采样表面湍流脉动压力、近场声压和远场声压，一共进行了2 500步的采样.计算在同济大学的1 352核高性能计算机集群下使用112核，花费5天.

2 结果分析

2.1 远场噪声

当瞬态流场达到统计意义上稳定后，以积分面的流场数据作为声源项对远场噪声进行预测.之所以采用积分面而非车体壁面，是因为它能够考虑地面效应和车体四周涡流噪声，从而基本实现与风洞试验相一致的条件.图5给出通过风洞试验和数值仿真得到远场测点2的声压级频谱.从图中可以看到，数值仿真结果与风洞试验结果变化趋势一致，量值相差不大.在能量分布上，声压级在较低频段和较高频段量值较小，约为60 dB(A)；声压级在中间频段(300～2 000 Hz)的量值较大，约65～70 dB(A).整个频段无明显峰值，表明远场噪声为宽频带噪声.

图5 测点2的声压级频谱Fig.5 Frequency spectral of sound pressure level of Test Point 2

数值仿真和风洞试验得到各测点的总声压级，如表1所示.从表中可以看到，测点2的总声压级分别为78.4 dB(A)和78.7 dB(A)，量值仅相差0.3 dB(A).靠近头车的测点1和靠近尾车的测点3的总声压级分别相差0.4 dB(A)和2.0 dB(A).由此可见，无论是测点总声压级，还是测点声压级频谱，数值仿真均能获得与风洞试验相一致的结果，表明基于FW-H方程预测远场噪声的正确性.

表1 测点总声压级 dB(A)Tab.1 Total sound pressure level of test point dB(A)

2.2 近场噪声

2.2.1湍流脉动压力

湍流脉动压力级通过非定常流动计算表面静压脉动得到.湍流脉动压力以振动形式通过车身结构传入车内.通过了解头型区域湍流脉动压力分布可以明晰主要噪声源分布，从而为远场和车内提供降噪方向.图6给出鼻锥、排障器、转向架、雨刮凹槽和曲线部位的湍流脉动总压力级云图.总体特征如下：

(1) 以车头鼻锥为界，底部湍流脉动总压力级大于上部流线型脉动压力级.在底部结构中，排障器、转向架下部轮对和转向架舱的表面湍流脉动总压力级最大.车身曲线部位的表面湍流脉动总压力级小于其它部位，但由于其面积大，对车内贡献仍不能忽略；

(2) 转向架舱侧缘、后缘是转向架舱表面湍流脉动总压力级最大的位置，数值可达140 dB(A)左右，排障器底部表面湍流脉动总压力级最大值也可达到相同量级.较小的湍流脉动总压力级集中在鼻锥、挡风窗顶部等流动分离弱的边界层区域，量级约为100 dB(A).

图6 头型表面湍流脉动总压力级Fig.6 Total pressure level of turbulence fluctuation of head shape surface

为了明确湍流脉动总压力级形成原因，分别沿流动方向和高度方向等距离截取截面，给出图7a所示的涡量分布.从图中可以看出，气流经排障器进入转向架舱，与转向架相互作用形成各种尺度涡流，涡流强度大、所占区域广，基本充满了整个转向架舱.气流离开转向架舱后缘后，涡流量值仍较大，所占区域仍较宽，直至离开转向架舱较远处才逐渐减少.从图7b可以看到，气流从排障器末端两侧沿着转向架舱两侧形成侧缘涡，从转向架舱前端到末端，侧缘涡强度增加，所在区域扩大.正是如此剧烈的涡流才形成了图6所示转向架与转向架舱量级极大的湍流脉动总压力级.

a 涡量分布b 等涡量Q=400

图7头型区域涡量分布

Fig.7Vorticitydistributionofheadshaperegion

2.2.2近场声压

近场声压可通过声扰动方程计算得到.以声波形式作用于车内，虽然量级不如湍流脉动压力，但通过车窗、缝隙等路径直接传入车内，声传递效率更高，对车内噪声的贡献不可忽视.空间声场的形成不仅来自于车身表面湍流脉动压力，也来自于车身四周的流动分离形成脉动速度.图8给出头型鼻锥、排障器、转向架、雨刮凹槽和曲线部位的总声压级云图.总体特征如下：

(1) 量级较大的区域集中在转向架舱和转向架，该处是流动最紊乱，且由于转向架舱自身属于半封闭空腔，声源在此传播有被放大的作用并会产生空腔固有的噪声特性.正因如此，转向架舱的声压级比转向架大，量级超过120 dB(A)；

(2) 排障器的声压级比转向架和转向架舱小.值得注意的是，湍流脉动总压力级较大的雨刮槽并没有呈现较大的声压级.它仅比头型上表面顶部和平直段声压级稍大；

(3) 对比相同部位的湍流脉动总压力级和总声压级可以发现，前者变化范围更大，分布不如后者均匀.

图8 头型表面总声压级Fig.8 Total sound pressure level of head shape

图9为整个频段的总声压级云图.通过位于远场传声器阵列接收到声源辐射的噪声，再以一定算法反推回声源处，从而识别出声源大小.它的数值是声源辐射到阵列上麦克风的值.量级较大主要集中在头车转向架区域.对比仿真和试验结果发现，他们所对应位置相同，但量级差异较大，这是因为仿真直接计算出该处声压.可见，通过声扰动方程得到近场噪声分布结果是正确可行的.

图9 传声器阵列识别的噪声源Fig.9 Sound source identificated by microphone array

3 结论

开展了1∶8缩比三车编组气动噪声风洞试验和数值仿真，得到以下结论：

(1) 建立了与风洞试验相一致的1∶8缩比三车编组气动噪声仿真模型.通过大涡模拟得到头型关键部位湍流脉动压力，基于FW-H方程和声扰动方程得到远场与近场噪声，从而建立一整套头型气动噪声预测方法.

(2) 远场测点声压级频谱和总声压级，近场总声压级分布等仿真结果均与风洞试验结果相吻合，表明基于FW-H方程和声扰动方程预测远场和近场噪声的正确性.

(3) 时速250 km·h-1时，头型转向架区域的湍流脉动总压力级和总声压级量级最大，分别可达140 dB(A)和125 dB(A).高速列车气动噪声优化控制应首先对该转向架区域进行针对性控制.