基于改进的直方图均衡化与边缘保持 平滑滤波的红外图像增强算法

李贤阳 阳建中* 杨竣辉 陆安山

1(北部湾大学电子与信息工程学院 广西 钦州 535011)2(钦州市电子产品检测重点实验室 广西 钦州 535011)3(江西理工大学信息工程学院 江西 赣州 341000)

Difference enhancement High frequency component classification Local maximum

0 引 言

红外成像技术是利用热辐射差异来识别目标和背景，能较好地反映出场景中温度场信息[1-2]。该技术具有环境适应性强、隐蔽性好、抗干扰能力强等优点，被广泛应用于监控、侦查和医疗等军民领域[3]。但是，由于自身硬件设备的限制和环境干扰，图像成像质量不高，总是受到低对比度、模糊细节和背景噪声的影响[2-3]。因此，增强红外图像的微弱边缘和抑制背景噪声是至关重要的，对于改善红外图像的视觉质量与后续的信息提取分析具有重要意义[4]。近年来，学者们提出了一系列的红外图像增强方案，这种技术不仅成本低，而且已经成为改善红外图像质量或增强表现的一种便捷方法，如Jaspreet等[5]为了改善红外图像的视觉质量，提出了一种用于红外图像的非训练对比度增强技术，通过优化的温度阈值来消除背景干扰，并通过去相关对比度拉升方法来进行颜色增强，实验结果验证了其算法的增强性能。这种基于对比度拉升的增强方法虽然结构简单，但其采用了一个固定的变换函数，缺乏自适应性，易导致增强图像的细节不清晰，且难以有效消除噪声。为了克服这个不足，基于直方图均衡化的增强技术得到了广泛研究，它是通过均匀分布待增强图像的概率密度函数来实现的，如曹美等[6]为了提高红外图像的低对比度与消除噪声，提出了改进的直方图均衡化和NSCT变换的红外图像增强。利用NSCT变换来获取待增强图像的高频子带系数和一个低频子带系数；利用自适应降噪函数与非线性增益函数来增强高频子带，以消除噪声与保留边缘信息；利用改进的直方图均衡化机制来增强低频分量。实验结果表明该技术增强了图像对比度，突出了图像的边缘轮廓信息。该技术通过利用视觉感知主观偏好特性来改进直方图均衡化的灰度映射，可以较好地提高全局对比度，但其忽略了高频分量的特性，利用同一个增强方法来处理所有的高频系数，导致其局部对比度增强效果较弱。Wan等[7]为了能够同时提高红外图像的全局与局部对比度，提出了基于粒子群优化的局部熵加权直方图均衡化的红外图像增强算法。利用基于改进的双曲正切函数来定义一种新的局部熵加权直方图，充分描述图像的细节信息分布；通过阈值最大化类间方差，将直方图分成两部分，分别改善前景和背景的对比度；同时，为了避免过增强和噪声放大，利用粒子群优化算法来形成双平台阈值直方图；最后根据带约束的子局部熵加权直方图，分别实现子图像的均衡化处理。实验结果验证了其算法的合理性与先进性。但是，该技术是一种空域增强方法，且其双平台阈值直方图均衡化方法中的阈值是固定的，对于红外图像不同的区域，缺乏自适应性，会出现过渡增强现象。

为了解决上述不足，兼顾增强图像的全局与局部对比度，并有效抑制噪声，本文提出基于改进的直方图均衡化与边缘保持平滑滤波均衡化的红外图像增强算法。所提技术是一种空域与频域相结合的增强方案。通过采用边缘保持平滑滤波来分解红外图像，输出一个低频分量和一个高频分量序列。为了最大化改善低频和高频分量的增强效果，本文利用不同的增强策略来处理各种成分。对于低频分量，利用模糊统计理论来确定出最优阈值，利用优化的平台直方图来增强低频分量，最大程度提高红外图像的全局对比度；根据高频分量的标准差，设计三个不同的增强方法，对其相应的系数进行差异增强，获取增强的高频分量序列，有效扩大红外图像的局部对比。通过非局部均值滤波来充分抑制噪声。最后，对所提增强方案的性能进行了验证。

1 本文红外图像增强算法

基于改进的直方图均衡化与边缘保持平滑滤波均衡化的红外图像增强算法过程见图1。依图可知，所提增强方案主要有4个阶段：(1) 基于边缘保持平滑滤波的图像分解；(2) 基于改进的直方图均衡化的低频分量增强；(3) 基于系数分类的高频分量差异增强；(4) 基于非局部均值滤波的噪声抑制。

图1 本文算法的增强过程

1.1 基于边缘保持平滑滤波的图像分解

边缘保持滤波[8-9]作为一种多尺度分解方法，可以较好地保持边缘并平滑图像、消除伪影，被广泛应用于数字图像处理领域。与其他经典的滤波器不同，边缘保持滤波可以有效地平衡锐化和模糊。令初始图像为S，通过边缘保持滤波，寻找出尽可能与S相接近的滤波图像I。滤波图像I的计算函数为[9]：

(1)

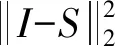
依据文献[9]可知，将式(1)进行如下转换，可得滤波图像I为：

I=G(S,λ)=(E+λH)-1S

(2)

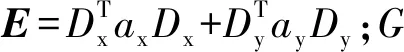
根据式(2)可知，当λ取大值时，可以获取平滑滤波图像。因此，边缘保持滤波可以实现多尺度图像分解，其过程见图2。对于给定的红外图像S，利用C个不同的正则化参数λi,i=1,2,…,C，基于边缘保持滤波，可获取C个滤波图像Ii,i=1,2,…,C：

Ii=G(S,λi)

(3)

式中：λi+1>λi。

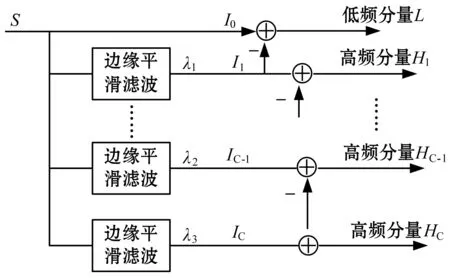
图2 基于边缘保持平滑滤波的图像分解过程

根据式(3)得到的滤波图像Ii，通过计算两个相邻Ii与Ii+1之间的差异，即可得到对应的高频分量Hi：

Hi=Ii-Ii+1i=1,2,…,C-1

(4)

式中：I0为初始图像。

以图3(a)为例，设置两个正则化参数λ=8、λ=20，利用上述过程对其完成分解，形成的低频分量见图3(b)，依图可知，低频分量包含了初始红外图像的绝大部分细节。经过λ=8、λ=20的平滑结果分别见图3(c)和图3(d)；通过式(4)计算，形成的高频分量分别见图3(e)、3(f)。

(a) 初始图像 (b) 低频分量

(c) λ=8的平滑图像(d) λ=20的平滑图像

(e) (a)与(c)之间 的高频分量 (f) (a)与(d)之间 的高频分量图3 基于边缘保持平滑滤波的图像分解

1.2 基于改进的直方图均衡化的低频分量增强

根据图3(b)可知，红外图像的全局视觉主要集中在低频分量上。而平台直方图均衡化PHE(Plateau histogram equalization)方法[10]作为传统直方图均衡化HE(histogram equalization)的改进版，它通过一个平台阈值来抑制背景增强，可以有效增强全局对比度。对于灰度等级为L的红外图像，其概率密度函数P(k)为[10]：

(5)

式中：k是第k个灰度等级；Nk代表图像中灰度等级为k的像素数量；N代表图像中总的像素数量。

在PHE方法中，其对应的概率密度函数为[10]：

(6)

根据式(6)可知，当P(k)≥T时，PHE方法中的P(k)主要是根据阈值T来设定；反之，则P(k)保持不变，始终等于阈值T。

基于式(6)，低频分量经过PHE处理后，输出结果为：

(7)

式中：DT(k)是增强后的第k个灰度等级；flood()代表向下取整运。

可见，在PHE方法中，阈值T对提高增强质量是非常重要的。但是，传统的PHE采用了一个固定的阈值，缺乏自适应性。为了能够根据不同的红外图像来选择不同的阈值T，本文利用模糊统计理论[11]对其改进。选择阈值T的关键因素就是找到图像直方图中的局部最大值[12]。然而，传统的直方图方法会产生锐化直方图，使其难以找到真实的局部最大值。而红外图像强度等级的不确定性可以用模糊统计来处理[13]。这种方法产生较为平滑的直方图，从而可以很容易确定这个局部最大值。以图3(a)为例，其对应的直方图见图4(a)，通过模糊统计处理的平滑直方图见图4(b)。依图可知，图4(b)比图4(a)更加平滑。

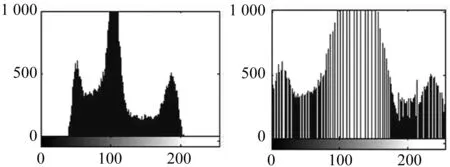
(a) 初始直方图 (b) 均衡化直方图图4 基于模糊统计优化后的均衡化直方图

在传统的直方图中，其p(k)反映了灰度等级k的频率；经过模糊统计优化后的p(k)则是表示灰度等级k周围的强度水平出现的频率。令B′(x,y)代表灰度值B(x,y)的模糊数量，则利用模糊隶属函数对B′(x,y)进行模糊化。依据文献[13]可知，经过模糊统计优化的直方图为：

(8)

(9)

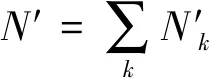
随后，根据式(8)计算得到的模糊直方图后，求取其一阶偏导：

(10)

式中：p(k)是模糊直方图P′(k)的一阶偏导。

则其相应的局部最大值kt可由如下函数计算：

kt=k∀{p(k)>0,p(k+1)<0}k=1,2,…,255

(11)

再利用中值滤波处理这些最大值对应的直方图上，从而得到最优平台阈值T：

T=M{P′(i1),P′(i2),…,P′(iS)}

(12)

式中：S为局部最大值的数量。

最后，根据式(5)-式(7)，联合优化的平台阈值T，对低频分量L完成增强：

LE=D(L)

(13)

式中：LE为增强低频分量；F(L)是模糊平台直方图均衡化。

1.3 基于系数分类的高频分量差异增强

高频分量中的大量系数与强边缘、中边缘、弱边缘对应[14]。也就是说通过改变高频分量的系数，即可增强边缘，完成局部对比度增强。首先，根据高频分量的标准差，将高频分量序列分类为三种边缘：

(14)

式中：Hk(i)代表第k个高频分量在位置i的系数；SEC是强边缘；MEC代表中边缘；WEC为弱边缘；σ为高频分量Hk的标准偏差；c为常量，本文取c=1。

随后，根据这三类边缘，设计3个增强策略，通过改变其系数Hk(i)，对这些高频分量实现差异增强：

(15)

式中：p为常量，通过多次测试，取p=0.9。

最后，将增强的低频分量LE与高频分量HE(i)(i=1,2,…,C-1)实施组合，输出增强图像：

IE=LE+HE(1)+HE(2)+…+HE(C)

(16)

以图3(b)、(e)、(f)为对象，利用上述处理过程，得到的低频增强结果见图5(a)，可见，红外图像的全局对比度明显提升；增强的高频分量见图5(b)、5(c)。可发现，红外目标的局部对比度明显改善。最终形成的增强图像见图5(d)。

(a) 增强的低频分量(b) 第一个高频的增强结果

(c) 第二个高频分量的增强结果(d) 输出的增强图像图5 图像的增强结果

1.4 基于非局部均值滤波的噪声抑制

由于红外图像中通常含有噪声干扰，因此，为了在增强图像的同时也可以有效抑制噪声，本文引入非局部均值滤波来实现[15]。非局部均值滤波[15]不仅可以强有力地消除噪声，而且还能保持图像边缘。令z(i)是原始图像中的位于i位置的像素，则其非局部均值滤波结果为Q(i)：

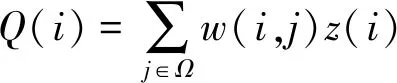
(17)

式中：Ω为图像域；w(i,j)代表两个相邻像素之间的权重值：

(18)

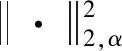
(19)

以图5(d)为对象，利用上述过程，对其完成噪声抑制处理，结果见图6。增强结果中噪声被有效消除，视觉更加自然。

图6 噪声抑制结果

2 实验结果与分析

为了反映本文算法的增强视觉质量，借助Matlab软件对其完成验证，另外，为了突出该算法的优势，将经典的直方图均衡化方法、文献[6]和文献[7]作为对照组。考虑一般性，从MORRIS图像库[16]中选择3幅图像作为测量目标；实验条件为：DELL电脑, 3.5 GHz，双核CPU，500 GB硬盘与8 GB内存。实验参数设置为：滤波图像数量C=2、正则化参数λ1=0.03以及λ2=0.1、c=1、p=0.9、权重αx=αy=0.8。

2.1 红外图像增强效果

以图7(a)、图8(a)、图9(a)为对象，基于所提算法、经典的直方图均衡化HE(histogram equalization)方法、文献[6]和文献[7]的方案对三种完成增强处理，结果如图7-图9所示。从图7可发现，初始红外图像的整体对比度较低，建筑物较为模糊，经过4种方案增强后，其对比度与细节清晰度均有所提高，然而，本文方案的增强效果最好，全局与局部对比度最高，细节更加清晰度，更好地保持了建筑物的边缘与细节，无过渡增强现象，见图7(e)。而经典的HE方法虽然改善了视觉质量，但是存在过度增强，见图7(b)；文献[6]虽然改善了红外图像的全局对比度，但是局部对比度较低，建筑物的清晰度不理想，细节与边缘有所丢失，整体视觉质量不自然，见图7(c)。文献[7]的整体增强效果较好，但是局部细节的清晰度有待提升，见图7(d)。在图8中，所提算法的视觉效果非常自然，兼顾了全局与局部对比度的平衡，见图8(e)；而经典的HE方法中存在局部过渡增强，见图8(b)；文献[6]的增强结果的局部对比度较弱，细节清晰度不佳，见图8(c)；文献[7]的整体视觉较好，但局部增强效果有待进一步提高，要略低于所提算法，见图8(d)中的方框。图9是高斯噪声干扰下的低质量红外图像增强效果。从图中可发现，对于含有噪声的红外图像，经典的HE方法不仅会出现局部过度增强，而且输出结果中仍在背景噪声，见图9(b)；文献[6]的增强效果要优于HE方法，但其局部对比度不理想，丢失了部分细节信息，见图9(c)；文献[7]的增强结果中的局部细节有待进一步增强，见图9(d)；而本文方案的增强视觉质量很好地兼顾了全局与局部对比度，细节清晰可见，而且有效消除了噪声，见图9(e)。原因是本文算法采用了边缘保持平滑滤波来分解红外图像，使得低频与高频分量更好地保持边缘，并得到了较好的平滑效果，且采用模糊统计理论来获取平滑直方图，根据其确定出局部最大值来改进平台直方图，以此完成低频分量，使其自适应较强，可以根据不同特性的红外图像确定合适的阈值，提高了全局对比度。另外，基于高频分量的标准差，设计三个不同的增强方法，对高频分量的三类系数进行差异增强，显著提高了局部对比度，从而保留了大量的细节。并且采用了非局部均值滤波来消除图像中的噪声，从而使其整体增强效果最佳。而经典的HE方法是对所有的像素进行相同程度增强，容易出现局部过渡增强现象。文献[6]算法则忽略了高频分量的特性，利用同一个增强方法来处理所有的高频系数，导致其局部对比度增强效果较弱。文献[7]采用的双平台阈值直方图均衡化方法中的阈值是固定的，无法根据红外图像特性来选择出较优的阈值，使其增效效果要略低于所提算法。

(a) 初始红外图像 (b) HE增强结果

(c) 文献[6]的增强结果(d) 文献[7]的增强结果

(e) 所提算法的增强结果图7 海上建筑红外图像的增强结果

(a) 初始红外图像 (b) HE增强结果

(c) 文献[6]的增强结果(d) 文献[7]的增强结果

(e) 所提算法的增强结果图8 城市红外图像的增强结果

(a) 初始红外图像 (b) HE增强结果

(c) 文献[6]的增强结果(d) 文献[7]的增强结果

(e) 所提算法的增强结果图9 噪声干扰下的红外图像的增强结果

2.2 增强效果的客观评价

为了客观量化这些增强结果的差异，本文引入模糊线性指数[17]、熵值[18]、标准差[19]来评估。模糊线性指数γ反映红外图像中有效信息量与对比度大小的指标，其值越小，表明增强质量越高，所增强图像的有用信息更多，对比度更高，所含的背景信息更少，其函数为[17]：

(20)

式中：fij代表像素(i,j)的灰度值；fmax是图像f的最大灰度值；M×N为图像f的尺寸。

熵值[18]能客观反映出增强红外图像的细节，熵值越大，则表明增强图像含有更多的细节，其函数为：

(21)

式中：p(mi,j)是像素灰度为mi,j出现的概率；M、N分别是图像的高与宽。

另外，标准差主要是反映红外图像对比度的有效指标，其值越大，说明增强图像的对比度越高，其函数为[19]：

(22)

表1显示了所提增强方案与其他三种方案对图7(a)、图8(a)、图9(a)的增强图像所对应的模糊线性指数γ、熵值H与标准差δ。由表可知，所提算法的增强图像对应的H、δ值均要大于文献[6]与文献[7]技术，而模糊线性指数γ均低于其他三种技术，但是，其δ值要低于经典的HE方法。对于图7(a)，所提算法的增强图像对应的H、δ分别为6.82、5.39，而γ值最低，为0.231。经典的HE方法虽然H值要低于所提方案，但由于其存在过渡增强，使其δ值要大于本文方案，分别为4.91、5.60、0.279。文献[6]的H、δ与γ值分别为5. 69、4.66、0.262。文献[7]的H、δ与γ值分别为6.34、4.87、0.255。尤其是在噪声干扰下，所提算法的优势更大，经典的HE方法的增强图像丢失了大量细节，其H值仅有4.26，而模糊线性指数γ达到0.293。而本文算法的H、δ与γ值保持较为稳定，分别为7.08、5.69、0.194。文献[7]的H、δ值也要远低于所提技术，分别为6. 41、5.05，对应的γ值也要高于所提技术，为0.220。

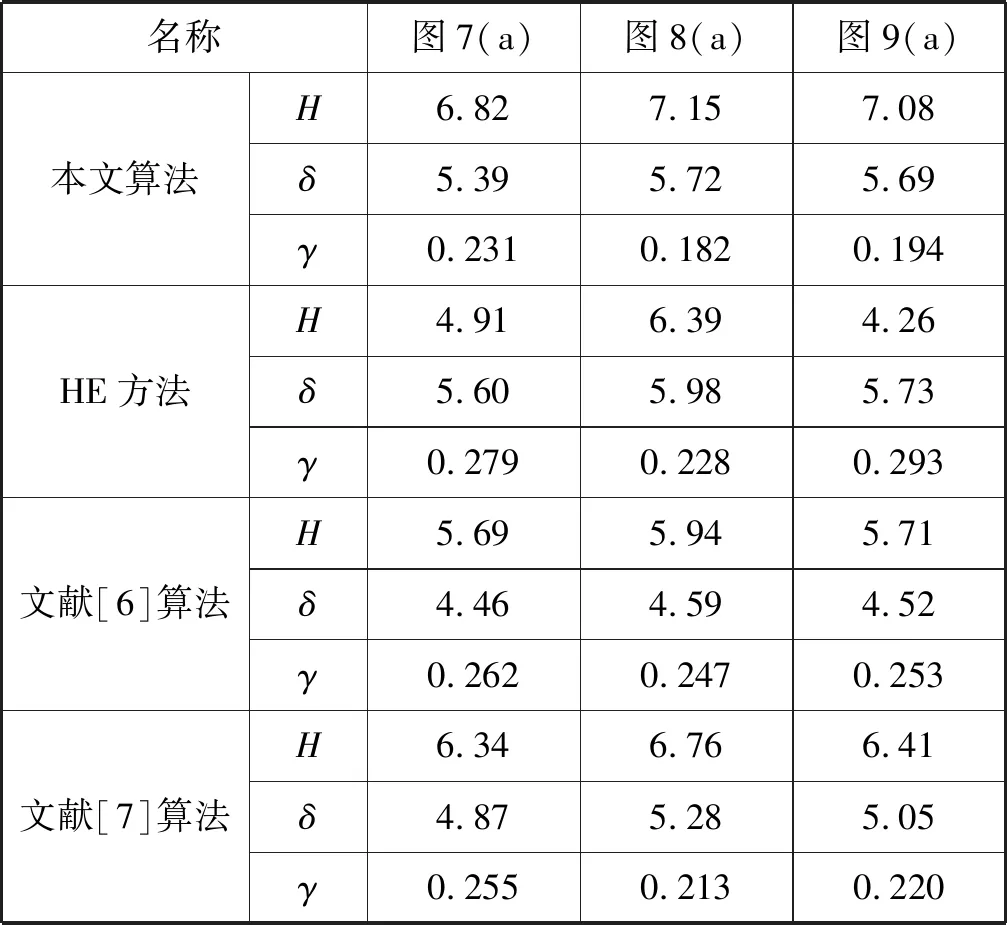
表1 不同算法的增强图像对应的模糊线性指数、熵值与标准差测试结果

3 结 语

为了提高红外图像的增强视觉质量，本文提出了基于改进的直方图均衡化与边缘保持平滑滤波的红外图像增强算法。利用边缘保持平滑滤波来分解红外图像，输出低频分量与高频成分序列。利用模糊隶属函数来改进平台直方图，根据其强度等级特性，确定出合适的阈值，提高了其适应性，以此对低频分量完成增强，从而改善了其全局对比度；根据高频分量序列的不同特性，设计了3个增强策略，对这些高频分量实施差异增强，以提高局部对比度，保留丰富的细节。为了消除噪声与保持边缘信息，引入非局部均值滤波对增强结果完成降噪处理。实验结果显示所提方法在主观视觉质量和客观评价方面均获得理想的结果。