相干信源DOA估计的一种改进空间谱估计算法

任生凯，刘尚钞，王开斌，周瑞青

(1.中国航天科工集团二院二十五所,北京 100854；2.中国人民解放军驻航天二院二八三厂军事代表室，北京 100854)

0 引言

战场上，反辐射导弹可以利用敌方雷达的电磁辐射信息进行跟踪导引，引导反辐射导弹飞行目标，摧毁敌方雷达及其载体，因而在战争中具有重要地位。但是随着现代战争的发展，战场环境日益复杂，受多径反射、敌方设置的有源诱饵干扰等因素影响，战场上同一时间、同一空域有时会出现多个相干信源，给反辐射导弹的目标来波方向(DOA)估计、目标跟踪等能力带来巨大挑战。研究如何有效解决多个相干信源的DOA估计问题，对提高反辐射导弹抗干扰能力、提升作战性能有重要意义。

为解决多个信源的DOA估计问题，从20世纪70年代末开始，超分辨空间谱估计在理论研究方面便出现大量成果，最有代表性的是Schmidt提出的多重信号分类(MUSIC)[1]算法以及Roy、Paulraj和Kailath提出的旋转不变子空间(ESPRIT)[2-3]算法。人们对这些算法的深入研究促进了子空间类算法的兴起。子空间类算法真正意义上实现了角度的超分辨估计，极大提高了DOA估计精度。但是，当面对相干信源时，绝大多数传统子空间类算法的性能迅速下降，甚至完全失效。

在相干信源情况下，要正确估计出信号方向，关键是如何有效地恢复阵列数据协方差矩阵的秩。目前关于解相干的处理大致可分为2类：降维处理和非降维处理。降维处理算法主要包括空间平滑类算法[4]、矩阵重构类算法[5-6]。降维类算法实现简单且解相干效果较好，但它们是以牺牲阵列的有效孔径为代价，导致阵列可分辨的最大相干信源数目变少。非降维处理算法包括Toeplitz算法[7]、最大似然(ML)[8]估计和加权子空间拟合(WSF)[9]算法等。其中Toeplitz算法的估计性能较差，ML和WSF算法思想简单且估计性能优越，但它们在求解过程中涉及到全局多维优化问题，计算过程相当复杂。

本文针对反辐射导弹的典型应用场景，对经典MUSIC算法的阵列接收数据模型进行了修正，提出一种改进的空间谱估计算法——MUSIC-TM。在相干信源情况下，MUSIC-TM算法破坏了经典MUSIC算法接收数据协方差矩阵各列之间的相关性，使其恢复为满秩，因而具有在反辐射导弹典型应用场景下解相干信源的能力，且计算复杂度无明显增加。使用Matlab软件对MUSIC-TM算法进行仿真，验证了该算法在实际应用中的可行性。

1 系统模型及经典MUSIC算法

基于MUSIC-TM算法的测向系统组成框图如图1所示。系统由接收天线阵列、多通道接收机、模数变换模块和内置了MUSIC-TM测向算法的数字信号处理器组成。接收天线阵列接收到多个信源来波信号，将其送入多通道接收机。信号在接收机中经过变频、放大，再经过模数变换模块得到数字信号，送入数字信号处理器，经过MUSIC-TM测向算法处理后，最终得到对来波方向(DOA)的估计。

图1 系统组成框图

1.1 相干信源模型

对于2个平稳信号si(t)和sk(t)，定义它们的相关系数为：

(1)

由Schwartz不等式可知|ρik|≤1，因此，2个信号之间的相关性定义为：

1)当ρik=0时，si(t)和sk(t)相互独立；

2)当0<|ρik|<1时，si(t)和sk(t)相关；

3)当|ρik|=1时，si(t)和sk(t)相干。

因此，根据上面的定义可以得到，当2个信号是相干信号时，它们满足式(2)：

si(t)=wisk(t)

(2)

式中，wi为一个复常数。

1.2 阵列信号模型

大部分研究者对MUSIC算法的研究多以一维均匀线阵为模型，但在反辐射导弹实际应用场景中，接收天线阵列安装方式一般为平面阵而非线阵，同时，目标信源可能的来波方向也分布在二维空间。因此，本文采用均匀环形阵列布局方式建立接收天线阵列模型，该阵列形式在国外反辐射导弹上较为常见。

考虑N个远场的窄带相干信号入射到由M个阵元组成的某空间环形阵列上(假设阵元数等于通道数)，其中各个信源来波方向分别为(φ1,θ1),(φ2,θ2),…,(φN,θN)，波长为λ，φ为方位角，θ为俯仰角。

信号源是窄带信号，因此信号可用如下形式表示：

(3)

式中，ui(t)是接收信号的幅度，ω0=2πf=2πc/λ是来波信号角频率，φ0是来波信号的初相。

因为窄带信号源是远场的，且信号源与接收天线阵列间相对位置关系不随时间变化，则有：

ui(t-τ)≈ui(t)

(4)

所以有式(5)成立：

si(t-τ)≈si(t)e-jω0τ,i=1,2,…,N

(5)

则可以得到第l个阵元的接收信号为：

(6)

式中，gli为第l个阵元对第i个信号的增益，τli为第i个信号到达第l个阵元时相对参考阵元的时延，nl(t)为第l个阵元在时刻t的噪声。理想条件下，不考虑阵列中各阵元的各向异性、通道不一致、互耦等因素的影响，可以认为式(6)中的增益gli相等，这里将gli归一化为1。

将M个阵元在时刻t接收到的信号写成一个列矢量，即：

(7)

τli仅与(φi,θi)有关，故式(7)可简写为：

X(t)=A(φ,θ)S(t)+N(t)

(8)

又由于s1(t),s2(t),…,sN(t)为相干信号，故式(8)可进一步简化为如下的矢量形式：

X(t)=A(φ,θ)Ws1(t)+N(t)

(9)

式中，X(t)为M×1维的阵列数据矢量，N(t)为M×1维的阵列噪声数据矢量，W为N×1维的复常数矢量，A(φ,θ)为M×N维的阵列流型矩阵(导向矢量矩阵)，即：

A(φ,θ)=[a1(φ,θ),a2(φ,θ),…,aN(φ,θ)]

(10)

式中，导向矢量ai(φ,θ)=[e-jω0τ1i,e-jω0τ2i,…,e-jω0τMi]H，i=1,2,…,N。

1.3 经典MUSIC算法

经典MUSIC算法的基本思想是将任意阵列输出数据的协方差矩阵进行特征值分解，从而得到与信号分量相对应的信号子空间和与信号分量相正交的噪声子空间，然后利用信号子空间与噪声子空间的正交性来估计信号来波方向等参数。该算法基于子空间分解思想，算法的基础是阵列采样协方差矩阵的特征值分解，算法的目标是计算空间角度谱。

阵列信号模型如式(7)所示，则阵列输出数据的协方差矩阵[1]为：

R=E[XXH]=AE[SSH]AH+E[NNH]=

ARSAH+RN

(11)

式中，RS=E[SSH]为信号协方差矩阵，RN=E[NNH]为噪声协方差矩阵。

对R进行特征分解：

(12)

式中，US为大特征值对应的特征矢量矩阵，称为信号子空间；UN为小特征值对应的特征矢量矩阵，称为噪声子空间。

理想条件下，信号子空间与噪声子空间是正交的，那么信号子空间的导向矢量也与噪声子空间正交，即：

aH(φ,θ)UN=0

(13)

经典的MUSIC算法正是根据式(13)这个性质提出的。但在具体应用中，考虑到实际接收数据矩阵是有限长的，只能得到采样数据协方差矩阵，即协方差矩阵的最大似然估计：

(14)

(15)

所以，MUSIC算法的DOA估计公式为：

(16)

根据信号参数范围进行谱峰搜索，找出极大值点对应的角度就是信号入射方向，这就是理想情况下的经典MUSIC算法。经典MUSIC算法一般只适用于理想条件下，而对于相干多源信号，经典MUSIC算法的理论基础不再成立。

2 MUSIC-TM算法

但是，1.2小节在推导公式(8)时，无形中假设了在阵列数据采样过程中，多个相干信源与接收天线阵列间相对位置关系不随时间变化这一前提。然而，考虑到反辐射导弹的典型应用场景，导弹在飞行过程中，每个信源到反辐射导弹接收天线阵列间的距离Li(i=1,2,…,N)都在时刻变化，且由于每个信源实际分布在空间不同位置上，故每个Li随时间的变化率不完全同步。此时，公式(7)中的τli不再仅与(φi,θi)有关，还同时与时间t有关，据此公式(9)修正为：

X(t)=A(φ,θ,t)Ws1(t)+N(t)

(17)

式中，A(φ,θ,t)为修正后的阵列流型矩阵(导向矢量矩阵)，即：

A(φ,θ,t)=[a1(φ,θ,t),a2(φ,θ,t),…,aN(φ,θ,t)]

(18)

这种对阵列接收数据模型进行修正后的MUSIC算法即为MUSIC-TM算法。

需要注意的是，MUSIC-TM算法中T的取值不能过大，否则在一次快拍采样过程中各个信源的来波方向将发生明显偏移，影响最终DOA估计的准确性。

3 性能仿真分析

为了验证MUSIC-TM算法的有效性，采用Matlab进行建模仿真。仿真场景中，假设反辐射导弹沿某一弹道向待打击的目标飞去，4个目标信源分布在反辐射导弹飞行方向前下方的地面上，并呈近似菱形分布，示意图如图2所示。

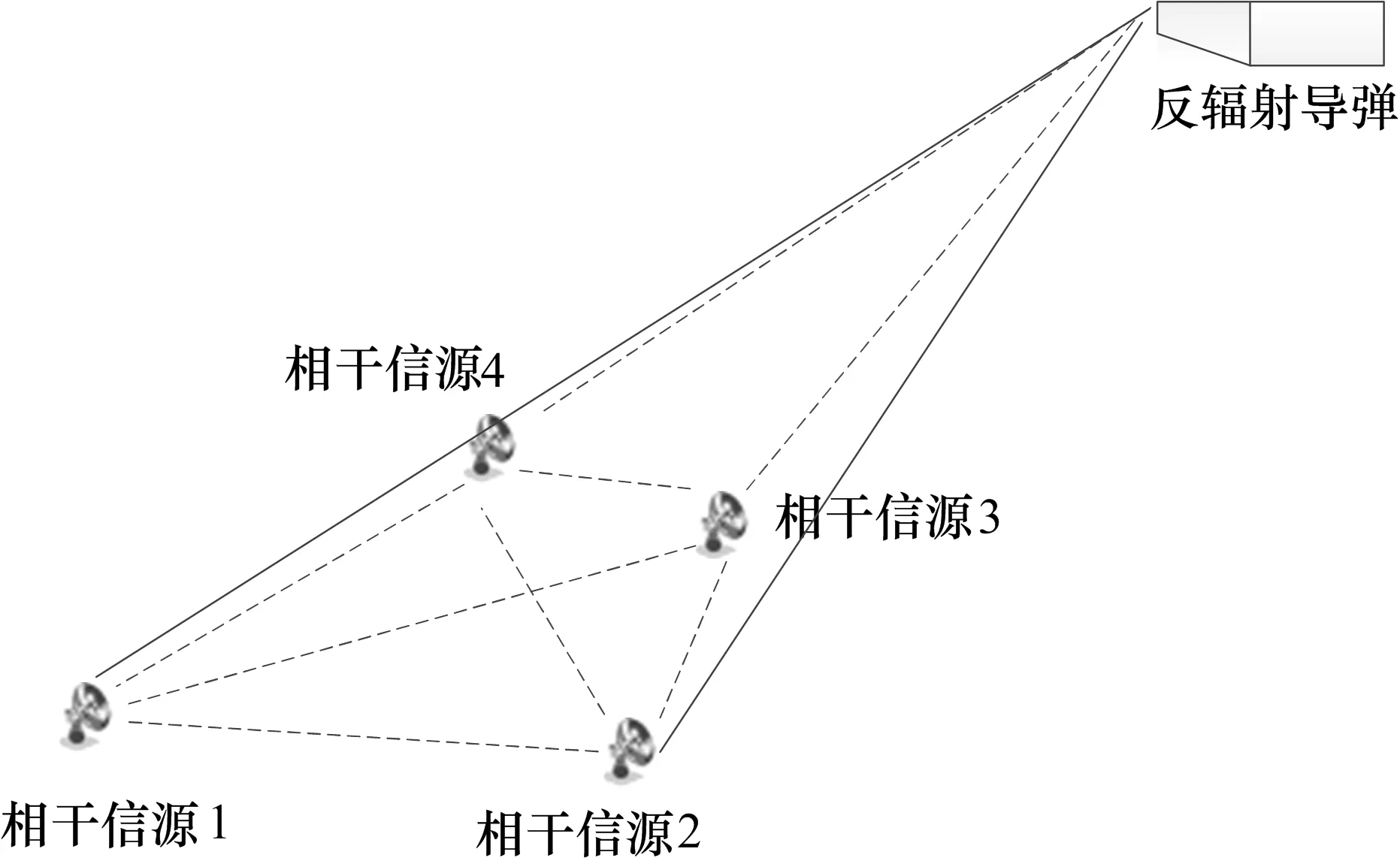
图2 仿真场景示意图

3.1 经典MUSIC算法仿真结果

在仿真中，令阵元数M=8，均匀环形阵列的直径为d=λ，目标信号源数N=4，C波段，噪声为均值为0、方差为1的高斯白噪声，信噪比20 dB，快拍数K=1000，采样快拍持续时间T=5 ms。经典MUSIC算法的仿真结果如图3所示。

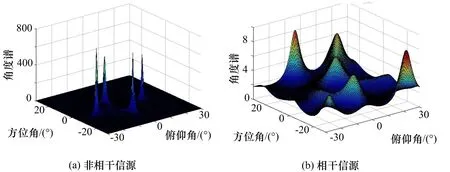
图3 经典MUSIC算法谱峰搜索结果

图3(a)为非相干信源下的谱峰搜索结果，图3(b)为相干信源下的谱峰搜索结果。由图3(a)可知，4个信源方向均呈现出较尖锐谱峰，说明经典MUSIC算法对非相干多源有较好的DOA估计能力。由图3(b)可知，当4个信源是相干信源时，谱峰搜索结果未在4个目标信源方向呈现出明显谱峰，谱峰搜索结果失败，说明经典MUSIC算法对相干多源没有DOA估计能力，这一结果与理论分析一致。

3.2 MUSIC-TM算法仿真结果

仿真参数设置与3.1小节中经典MUSIC算法相同，MUSIC-TM算法的仿真结果如图4所示。

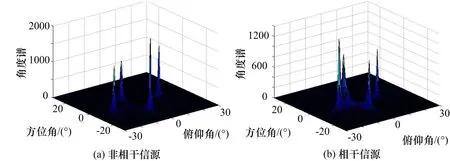
图4 MUSIC-TM算法谱峰搜索结果

图4(a)为非相干信源下的谱峰搜索结果，图4(b)为相干信源下的谱峰搜索结果。与图3(b)不同，当4个目标信源是相干信源时，在图4(b)中MUSIC-TM算法的谱峰搜索结果仍然呈现出4个较尖锐的谱峰，说明MUSIC-TM算法在相干信源DOA估计方面的性能远优于经典MUSIC算法。

由图4(a)可知，MUSIC-TM算法也同样可以对非相干信源进行DOA估计，其性能与经典MUSIC基本相同，符合理论分析的预期。

综上所述，MUSIC-TM算法具备一定的工程应用价值。

4 结束语

本文对经典MUSIC算法的阵列接收数据模型进行了修正，提出一种改进的空间谱估计算法MUSIC-TM，并通过Matlab仿真对MUSIC-TM算法的解相干信源能力进行了测试。仿真结果表明，在反辐射导弹典型应用场景下，MUSIC-TM能够克服经典MUSIC算法无法对相干信源进行准确测向的缺陷，对相干信源具有较好的DOA估计能力，为反辐射导弹抗多径干扰和相干有源干扰提供了一种有价值的方案。■