海面背景下低空目标电磁散射特性仿真技术
袁晴晴,阮开智,聂 丁,汪书阁,王冠坤
(1.上海机电工程研究所,上海 201109; 2.西安电子科技大学物理与光电工程学院,陕西 西安 710071)
0 引言
复杂海洋背景环境中掠海目标电磁散射机理及多径效应的研究是地海环境中目标信号识别和杂波信号分离技术的关键所在,与精确制导、低飞目标和舰艇目标的识别技术紧密相关,其应用涉及雷达成像、遥感技术、制导和预警等众多领域,是目前急需重点研究和解决的基础课题。在低空环境下,由于海背景的复杂性,目标探测系统性能会因为环境杂波引起的多径干扰而严重退化。本文基于散射机理的动态海杂波模型,开展海面背景下低空目标电磁散射特性仿真技术研究工作。
1 动态海面几何建模及散射特性分析
1.1 复杂海洋场景几何建模
传统海浪几何建模方法主要是以线性海浪理论为基础,从严格意义上来说,该类方法只能对单纯的风浪或者涌浪进行模拟,没有对更细微的波浪之间相互作用的非线性效应进行细致考虑。而实际海浪多以复合形态存在,即大尺度重力波和小尺度毛细波(如图1所示),另外加上风、浪及波-波间作用的非线性效应,海浪波面起伏在一定程度上会偏离高斯分布。由于考虑了波浪间的非线性水动力作用和长波、短波间的相互运动,非线性海面的形状和统计特性与线性海面是不同的,因而进一步通过海面起伏、波面斜率等信息对海面的电磁散射产生影响。本文基于Choppy Wave Model (CWM)建模方法模拟非线性海面,从基本的流体动力学方程出发,在水动力方程零阶解的基础上,通过希尔伯特变换运算来考虑相位扰动,最终通过该扰动项来计及海浪之间的非线性相互作用。
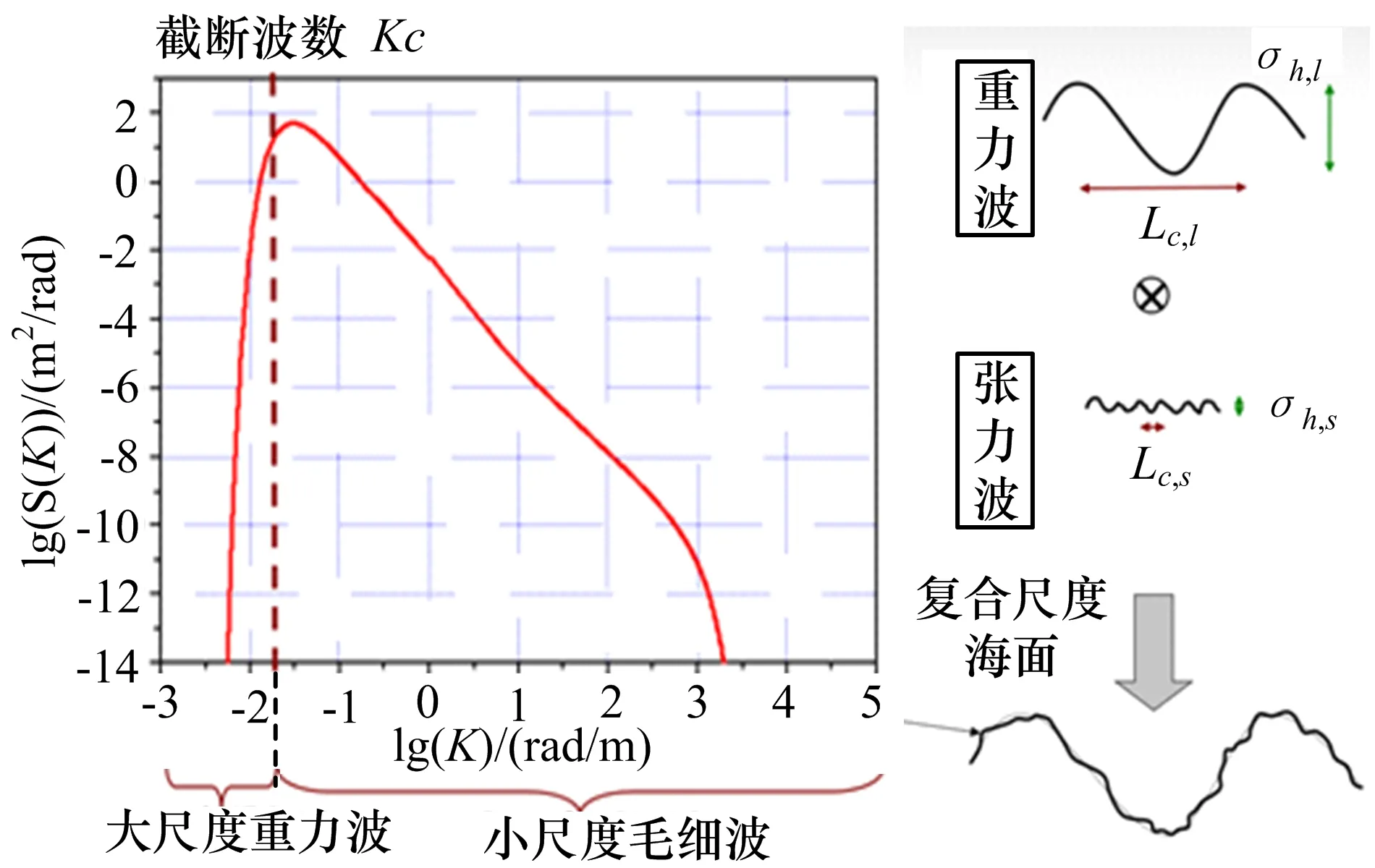
图1 复合尺度海面几何建模示意图
图2为一维线性海面和非线性海面起伏对比,风速为6 m/s。从图2可以看出,模拟的非线性海面呈现出了明显的斯托克斯非线性波特性:相对于线性海面而言,波峰高而陡峭,波谷浅而平坦。同一维海面的情况类似,图3中非线性海面波峰处(实线圈标记)较为尖锐而波谷处(虚线圈标记)较为平缓的特点同样得到了体现,只是该效果在二维海面的情况下体现得更加充分。
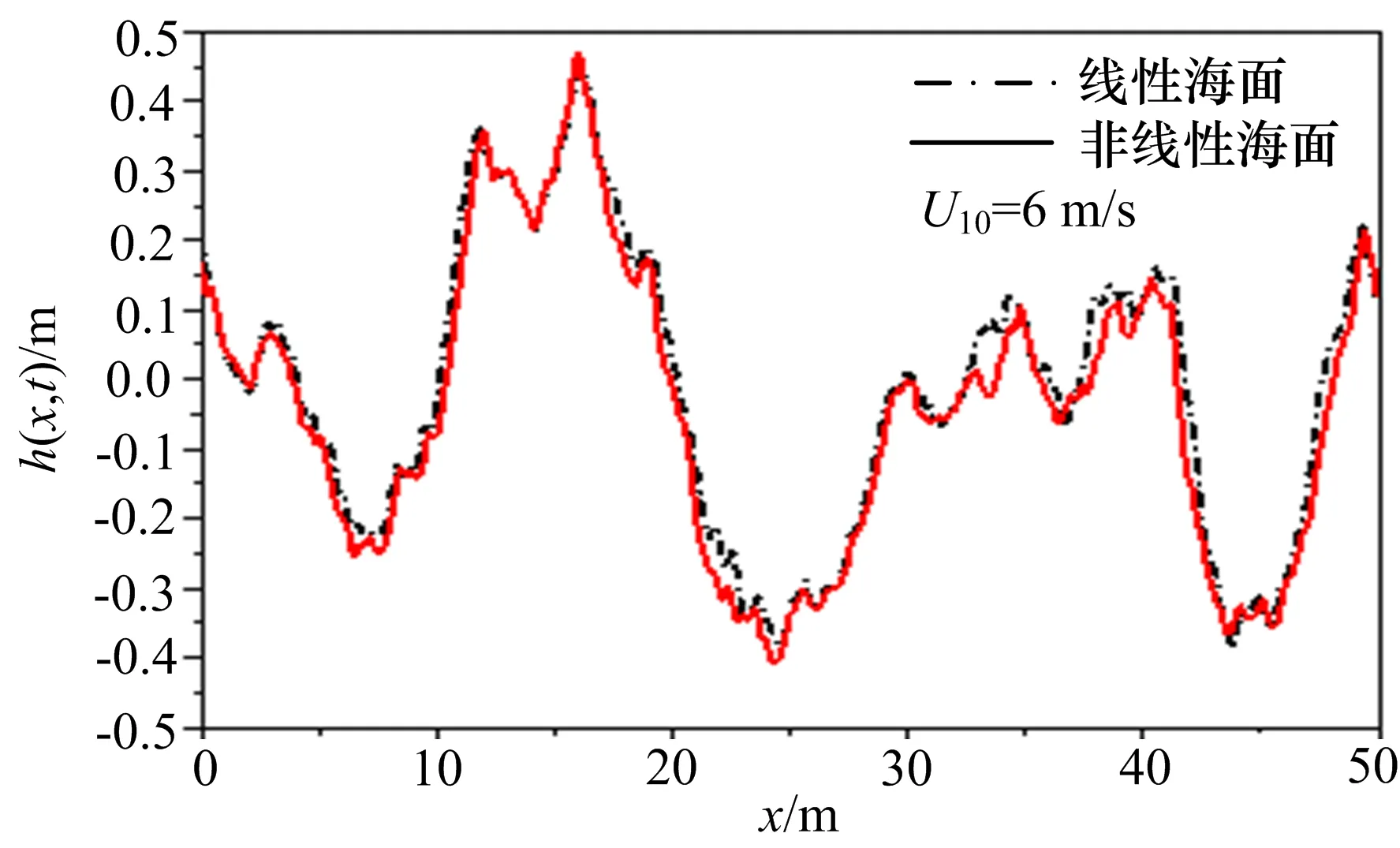
图2 一维线性海面和非线性海面起伏对比

图3 二维线性海面和非线性海面起伏对比
1.2 海背景的电磁散射特性分析
小斜率近似方法(SSA)是将散射幅度或雷达散射截面对粗糙面的斜率作幂级数展开,方法的精确度可以通过保留级数的项数来决定。作为一个统一理论模型, SSA很好地统一了微扰法(SPM)和基尔霍夫近似方法(KA),很适合计算具有大-中-小复合尺度粗糙度的海面散射问题,这非常有利于在多种电磁频段下对海面散射特性进行预估。此外SSA具有较高的计算精度,尤其在较大入射角情况下,比KA和SPM精确许多,并且相对于矩量法和积分方程等方法,计算公式相对简单,计算效率高。对于粗糙面电磁散射计算,一阶SSA(SSA-I)已经被证明有较高的精确度。二阶SSA(SSA-II)相对于SSA-I,表达式相对复杂,计算效率会有所下降,但其计算结果更加精确,且由于在SSA-I基础上考虑了更高阶项的影响,因此能够更好地对海面微尺度结构的散射特性进行考虑。在海面精确建模的基础上,本文针对传统的SSA进行了算法改进,使之能够适用于对非线性海面进行电磁建模。下面基于改进型小斜率近似方法完成多种入射角度下、不同海况时海背景的电磁散射特性分析,分析了不同雷达频率下的动态海面低掠角散射特性。
对海面电磁建模得到的计算结果进行验证,验证模型包括精确数值计算方法(MOMI)和研究领域内认可度较高的经过机载测量试验验证通过的SASS_II模型。图4为SSA-II和精确数值算法MOMI计算的一维线性海面双站散射系数随散射角的变化对比,仿真条件为风速7 m/s,入射角60°,入射频率3 GHz。图5为利用模型SSA-II和基于机载测量试验验证过的SASS_II模型的海面后向散射系数NRCS随散射角的变化对比。入射频率设置为14 GHz。从图4、图5的对比结果可以看出,SSA-II计算结果与测量数据和理论模型数据吻合良好,体现了较好的计算精度和较强的多频段计算性能。
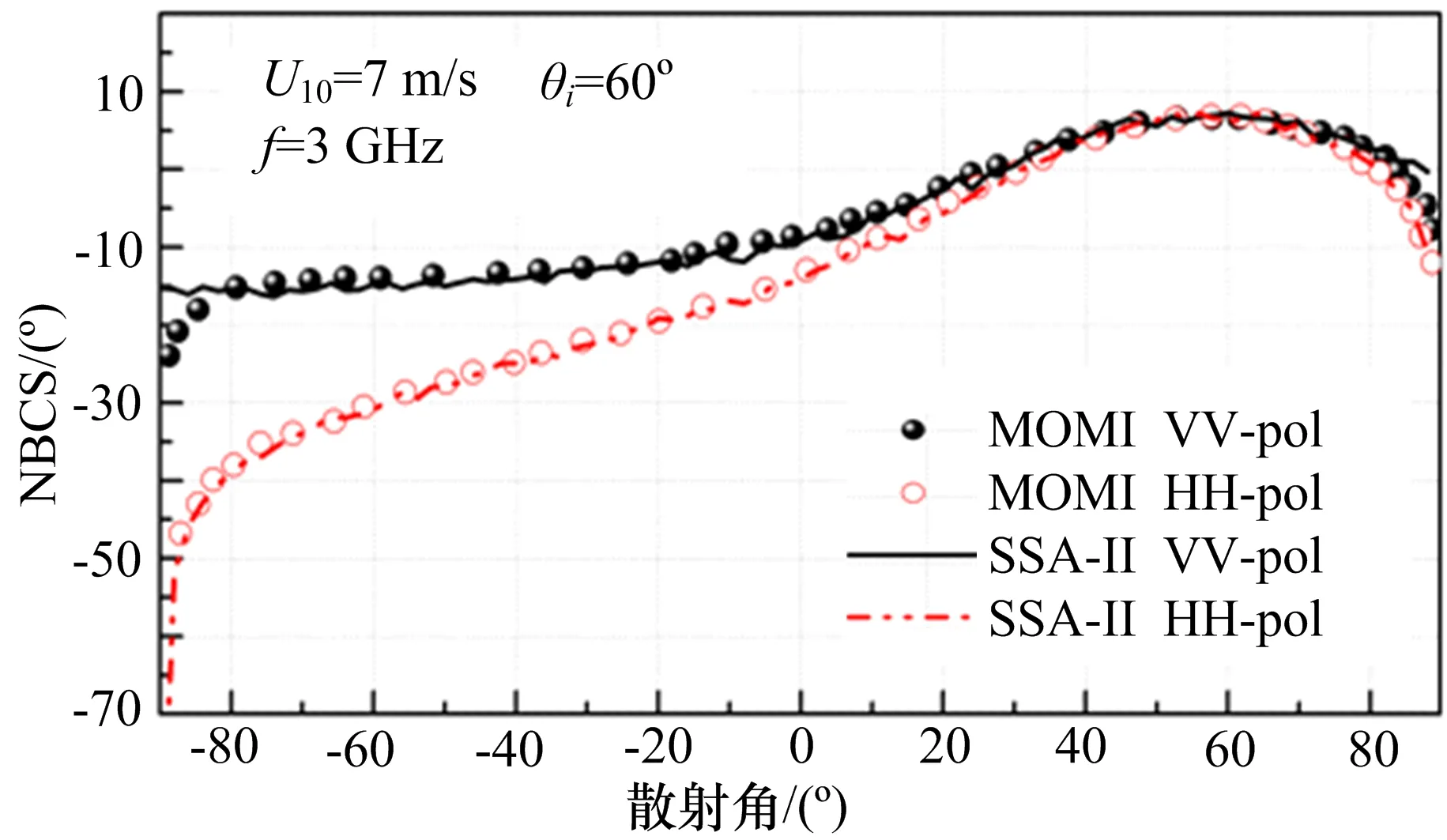
图4 SSA-II和MOMI方法计算的一维线性海面双站散射系数对比图
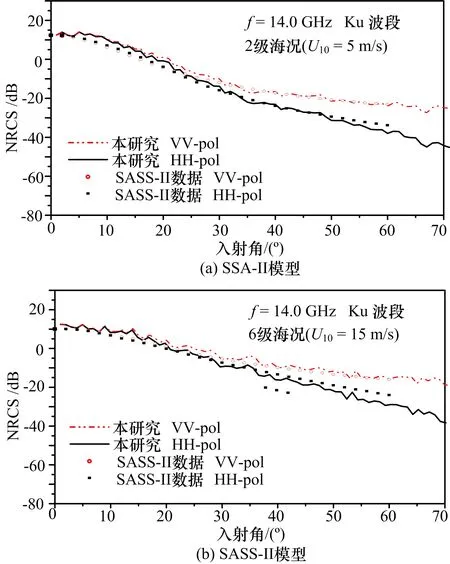
图5 SSA-II模型和SASS_II模型计算的海面后向散射系数对比图
图6对不同电磁波频率入射时的海面双站散射系数NRCS随散射角的变化进行了展示。其中风速为5 m/s,入射频率为1~26 GHz,覆盖了L、X、Ku和K波段。
2 类反舰弹与海面的复合散射特性仿真
2.1 目标与海面的复合电磁散射算法
本文通过GO-PO方法考虑目标与海背景耦合场的作用机理和多径效应,进行目标与海面的复合电磁散射建模。电磁波投射到目标或海面上,不仅考虑在反射方向产生的一次散射场,而且对反射方向进行追踪,直至到达下一个反射面,再次计算新的反射方向上的散射场。相比于传统精确数值方法,该方法计算效率明显提高,而计算精度并没有太多损失,适合进行高频段目标和海面复合电磁散射特性评估。下面采用GO-PO方法来对本文目标电磁散射的计算方法进行验证。图7中给出的是利用基于弹跳射线法的GO-PO方法计算得到的球-板目标组合体的复合单站RCS,入射电磁波的频率为10 GHz,可以看出计算得到的组合体目标RCS与实验测量值吻合良好,体现了算法的有效性。
2.2 类反舰弹目标与海面复合双站前向散射情况
类反舰弹目标几何形状示意如图8所示。弹体头部采用了2种平面结构对接组成。采用该平面结构而非传统曲面结构的弹头旨在对比计算出相应的散射强点分布。弹体尾部采用了凹形结构。2级海况时对应的仿真海面尺寸为20 m×20 m,而当海况等级增大时,海浪的起伏程度有所增加,对应的仿真海面尺寸增加为30 m×30 m。仿真中目标头部沿X轴正向放置,电磁波从后方投射到目标所在区域,观察方向位于目标前向。图9给出了仅考虑目标和海面单次散射的计算结果和考虑多次散射耦合场的计算结果对比,计算条件为2级海况(风速5 m/s)。可以发现在远离镜像散射方向区域(漫反射作用区域),考虑多次散射的回波RCS明显高于单次散射结果,体现了多次散射在低掠角情况下“目标+海面”复合散射计算中的必要性。
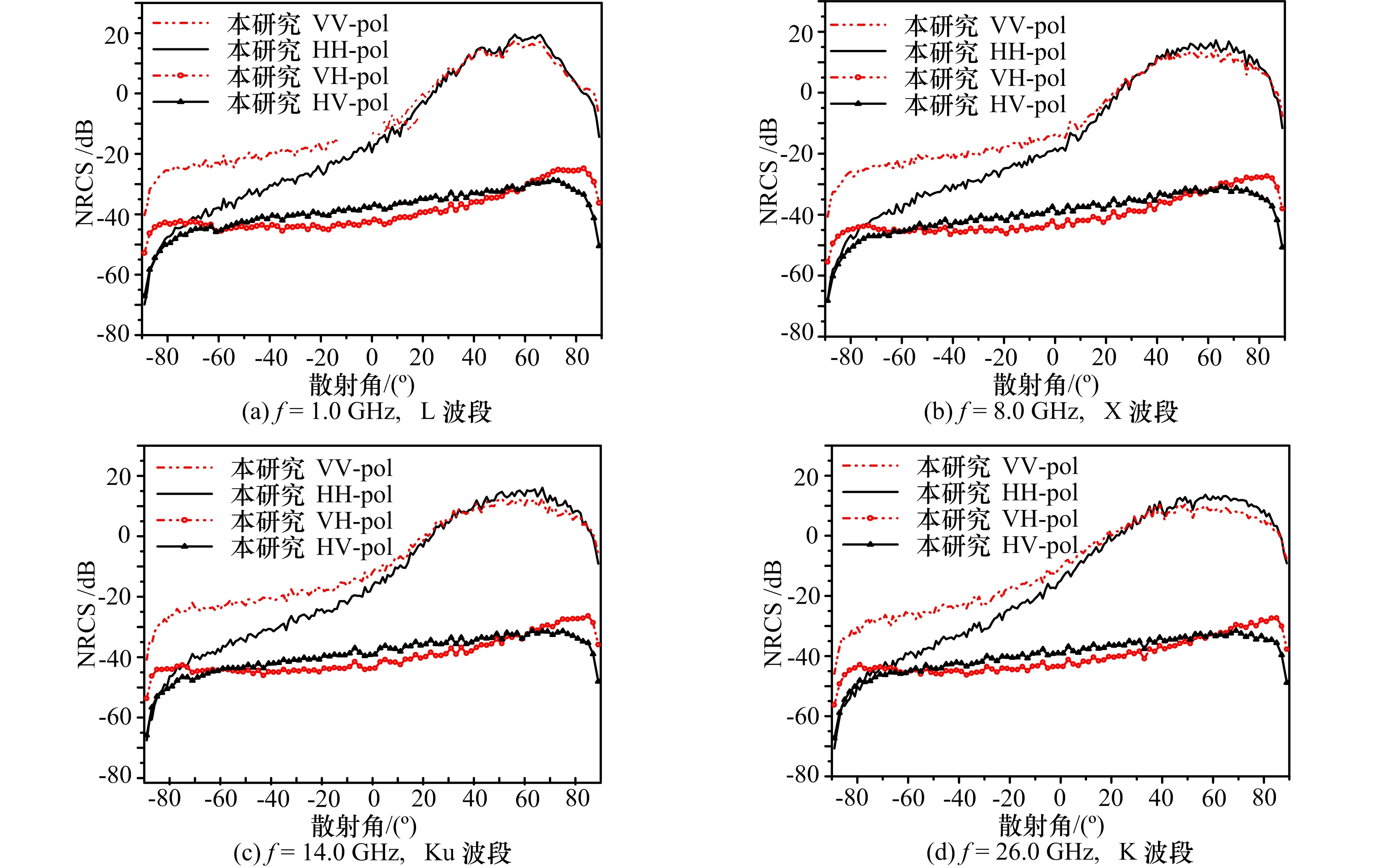
图6 海面双站散射系数NRCS随散射角的变化图
图10 给出了 1GHz、2级海况(风速5 m/s)时入射角分别为0°、30 °、45°、 70°、80°、85°时,类反舰弹和海面复合双站前向RCS随散射角的变化对比。
当雷达波以小于70°入射角到达目标与海面时,入射面内的绝大多数散射角度对应的复合散射回波RCS与海面的RCS量值差异很小,这就意味着这些角度下弹体的散射回波将湮没于海杂波之中。而入射角逐渐增大至70°时,HH极化情况下复合散射在远离镜向散射的角度(小于-50°)时才能体现出目标回波特征。
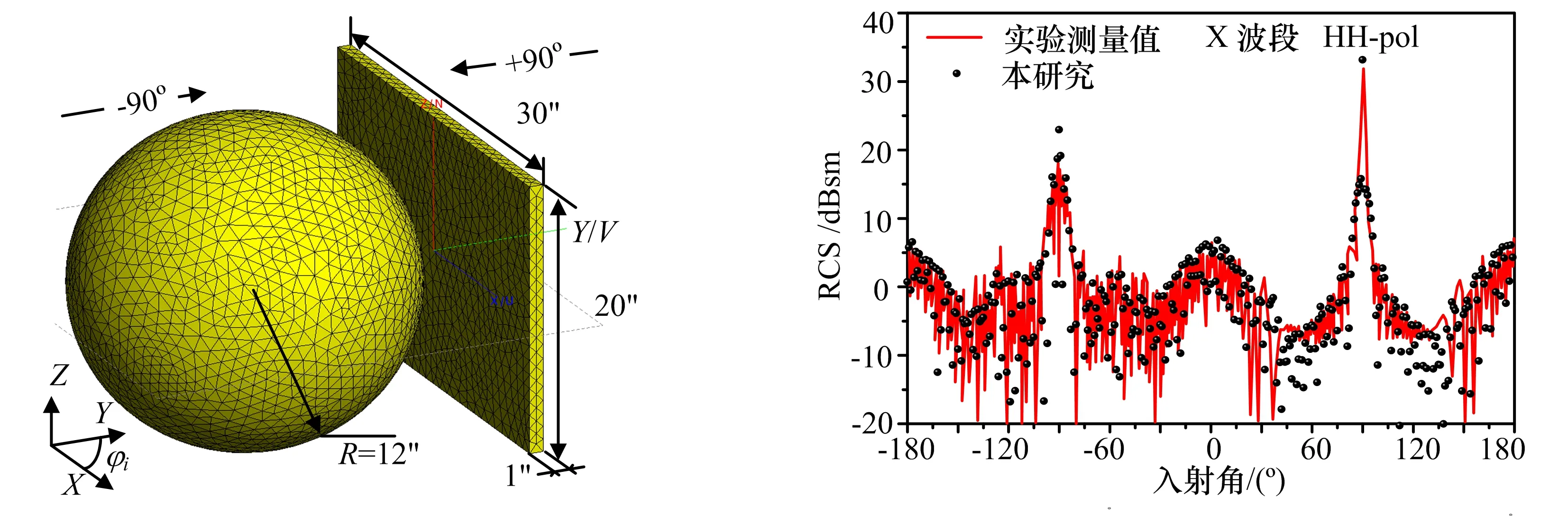
图7 球-板目标组合体的单站RCS与实测值的对比
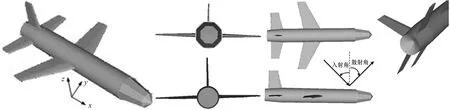
图8 类反舰弹目标几何结构示意图
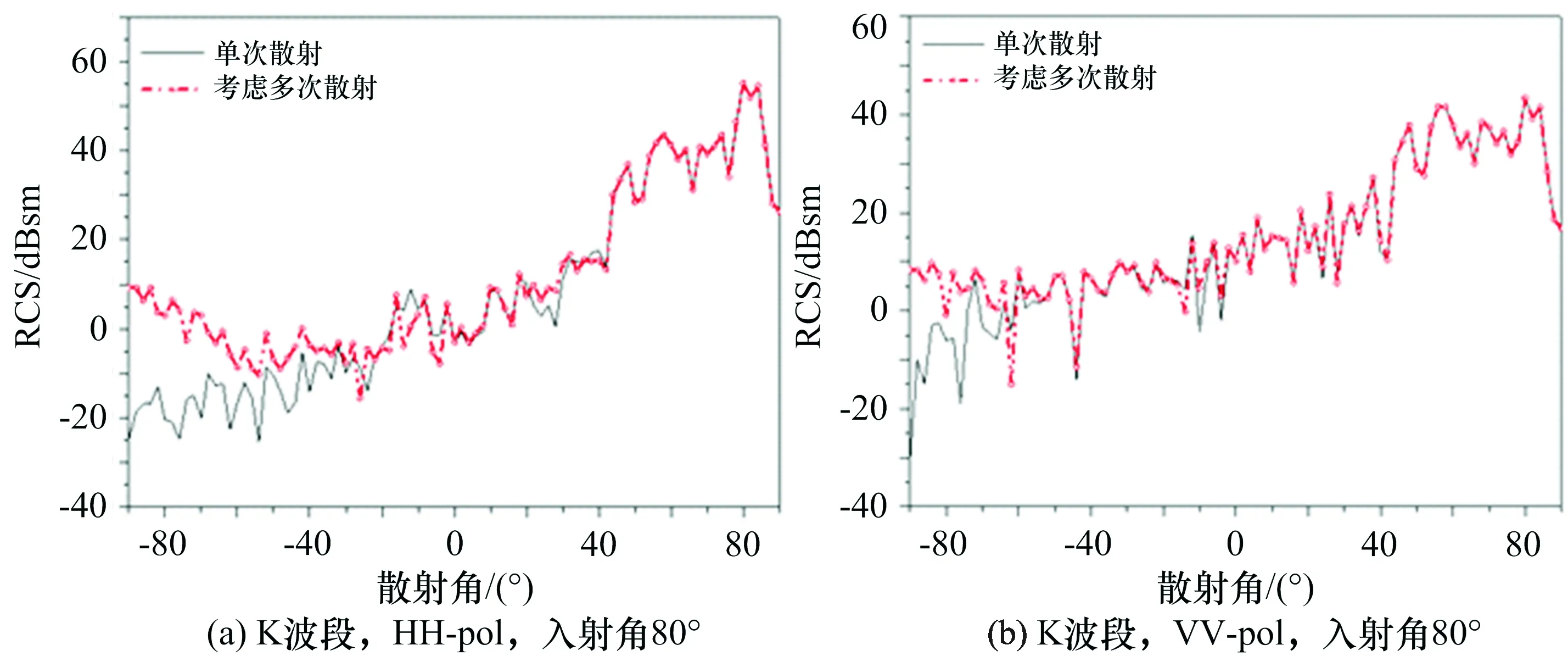
图9 “类反舰弹+海面”复合散射的单次散射和多次散射结果对比

图10 “类反舰弹+海面”复合双站前向RCS随散射角的变化对比
3 结束语
本文建立了基于散射机理的动态海杂波模型和复杂海洋场景的回波模拟,分析多种雷达电磁波极化方式下,雷达参数(尤其是低掠角情况下)和海环境参数对海杂波特性的影响,开展复杂低空目标反舰弹和动态海洋环境在低掠角情况下的电磁散射机理研究,获取目标与海背景的相干散射模型和特征参数。相比较于陆地背景杂波,海杂波具有明显的动态特性,因此可以对海杂波和运动目标回波的多普勒回波信号进一步开展深入研究。■

