数学深度学习如何真实发生

近年来，我们的教学在不断地尝试改革，如先学后教、翻转课堂等的出现就是如此。这种以强调学生自主学习为主的改革出发点是好的，但是在实际操作中，我们往往又会顾此失彼。例如，强调学生的兴趣而忽视系统知识的学习，强调学生的主动参与而忽视教师的引导，强调学生的愉悦而轻视严肃严格的学习，等等。于是，基于教学规律之上的探索就显得尤为重要，深度学习之研究即是如此。

我们认为，深度学习是指课堂教学中学生的学习而不是一般的学习者的自学，强调教师的引导和帮助。这是符合学习认知规律的，老师有相对系统的认知体系，懂得如何引导学生将学习走向深入。深度学习的内容是有挑战性的人类已有认识成果。例如，三角形的任意两边之和大于第三边，就这个问题而言，学生要理解它甚至运用它是富有挑战性的。从心理学的角度看，富有挑战性的活动会更吸引学生穷究到底的兴趣。深度学习是学生感知、思维、情感、意志、价值观全面参与、全身心投入的活动，而知、情、意是人类心理活动的三种基本形式，当知、情、意、行完美统一的时候就成了最恰当的教育。

由于深度学习是极为复杂的活动，在具体的教学实践中，如何知道深度学习发生了？或者说，我们从哪些方面努力就可能引发学生的深度学习呢？

一、联想与结构

我们可以从两个方面去理解联想与结构，一方面指学生学习方式的样态，另一方面指这样的学习方式所处理的学习内容。

作为学习方式的样态，说的其实就是如何把需要学习的知识系统与学生已有的经验系统建立起联系。教师要考虑的问题是如何调动学生已有的经验来参与当下的学习，又要将当下的学习内容与已有的经验建立起结构性的关联，从而使知识转化为与学生个体有关联的、能够操作和思考的内容，并进一步纳入新的认知系统。知识→联结→经验→新的经验→新的知识，这样的活动，就是深度学习。

例如，在教学“圆柱的体积”时，我们设计了这样一个活动：老师出示一张圆形纸片和一张长方形纸片，告訴学生，这两张纸片的大小一样，也就是面积相等。现在，我想把这样的100张圆形纸片与100张长方形纸片分别摞起来形成一个圆柱、一个长方体。比较这两个立体图形的体积，你认为哪一个会更大些？说说理由。

显然，这样的问题激活了学生已有的认知经验：底面积一样，高度一样，体积（物体所占空间的大小）肯定一样。在此基础上，老师进一步提出问题：“基于刚才的研究，你们能提出什么新的问题吗？”有学生提出，只要底面积相同（与形状无关），高度相同，体积一定相等。此时，老师追问：“果真如此吗？”通过操作和讨论，学生达成共识，只要底面积和高分别相等的柱体，体积一定相等。

这样教学，通过联想，激活学生已有的知识经验，以融会贯通的方式对学习内容进行重组，从而建构出自己新的知识结构，达到学一课知一类的目标。

二、活动与体验

活动与体验是深度学习的重要特征。这里的活动是以学生为主体的活动，不仅仅是动手操作，更多的是来源于学生头脑的思维活动。这里的体验指的是学生主动参与数学活动时的个体体验，当学生全身心投入时，这种体验是一种积极的有后劲的学习体验，是学生愿意持续进行数学学习的原动力。

我们强调学生要有活动的机会，特别强调要有亲身经历。当然，这种亲身经历不排除用头脑与心灵去模拟地、简约地经历知识的发生、发现、形成、发展的过程。华东师范大学张奠宙先生在《教育数学是具有教育形态的数学》一文中指出，数学具有三种形态：原始形态、学术形态、教育形态。原始形态是指数学家发现数学真理、证明数学命题时所进行的反复曲折的数学思考；学术形态是指数学家在发表论文时采用的形态，包括形式化、严密地演绎和逻辑地推理，它呈现出简洁的、冰冷的形式化的美丽，却把原始的、火热的思考淹没在形式化的海洋里；教育形态是指通过教师的努力，启发学生进行火热的思考，使学生更容易接受人类数千年积累的数学知识体系。我们认为，张奠宙先生提倡的教育形态的数学与深度学习在本质上是一样的，教师要充分发挥主观能动作用，设计适合深度学习的教学活动，让学生经历知识形成的过程。

例如，集合是近代数学中的一个重要概念，集合思想作为现代数学思想已向小学数学教材进行渗透。但是，集合思想对于小学生来说非常抽象难懂，要感悟是很困难的。那么，如何设计好的数学活动与数学问题，让学生在活动中领悟集合思想，并运用集合思想与方法解决实际问题呢？我们进行了这样的设计。

【课前准备】学生在卡纸上写自己的名字。

【教学过程】

活动一：棋子的秘密。

师：今天的数学课从游戏开始，先请同学们看这两个圆圈。（出示实物绿圆圈、红圆圈，绿圆圈里有4颗棋子，红圆圈里有3颗棋子）

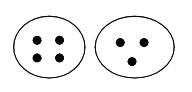
师：现在两个圆圈里一共是几颗棋子？

生：4+3=7，7颗。（板书：4+3=7）

师：对，这个游戏对于你们来说可能有点小儿科了。现在游戏马上升级，听好了，还是这两个圆圈，还是这7颗棋子，变一变，让绿圆圈里有5颗棋子，红圆圈还是3颗棋子。你会吗？

生1上台从红圆圈里拿1颗棋子放入绿圆圈。

师：老师采访一下你，为什么要从红圆圈里拿1颗棋子到绿圆圈里？

生1：因为绿圆圈里要有5颗棋子，现在只有4颗，所以得从红圆圈里拿1颗。

生2：不可以！这样子红圆圈里棋子的数量就不符合要求了！

生3：可以放中间。（师把棋子放在两个圆圈的中间，如图所示）

生4：不对不对。

师：哪里不对了？

生4：这样放的话，红圆圈里只有4颗，绿圆圈里只有2颗，它们都少了1颗棋子。

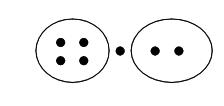
师：那这颗棋子到底怎么放？不要着急，有时静下心来想一想，你就会想到两全其美的办法。

热闹的课堂很快安静下来，同学们陷入了沉思。

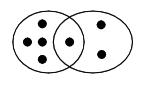
一生上台移动红圆圈，将两个圆圈交叉在一起，然后从红圆圈里拿出一颗棋子摆在中间交叉的部分（如图所示）。

学生欢呼起来：这样可以了！

师：什么叫可以了？

生5：你看！现在绿圆圈里有5颗棋子，红圆圈里有3颗棋子。

师：噢，今天老师长見识了，原来5加3还可以等于7。（板书：5+3=7）

学生交流讨论，发现中间的1重复计算了一遍。

师：你说的重复是什么意思？

生6：中间的这颗棋子，我们数5时数了它，数3时也数了它，多数了一次就是重复了1次，所以要减1。（板书：5+3-1=7）

师：那这个减1是不是把中间的棋子减掉？

生：不是，减去的是重复计算的那个1。

师：看来，这游戏一升级就有点意思了。

在这样的过程中，学生在掌握用重叠方法解决问题的同时，受到集合思想的启蒙。更重要的是，这些知识与方法的获取完全来源于学生自身的活动。学生在这样的活动中，不仅知其然也知其所以然，体会到交集策略的形成过程。在深度学习这里，教学不再是人们所讽刺的“颈部以上的”冷冰冰的理智活动，而是理智与情感共在的，鲜活的、有温度的活动，学生以全部的思想和精神去感受和体验学习活动的丰富复杂、细微精深。

三、本质与变式

把握事物的本质，是建构知识结构的前提。在把握事物本质的过程中，需要去除非本质属性的干扰，分辨出本质与非本质属性的区别，对学习内容（学习对象）进行深度加工。因此，对于数学内容的教学，我们不主张带领学生背诵数学定义与概念，而是要设计好的活动，让学生在活动中学会质疑、探究、归纳等等。在这些深层次的活动中，学生通过自身的努力逐渐逼近对事物本质的认识。

例如，我们在教学四年级“图形的面积与周长”这一内容时，为了让学生体会“面积可增减，而周长不可；周长确定的条件下，面积可变”这些认识，设计了下面的活动。

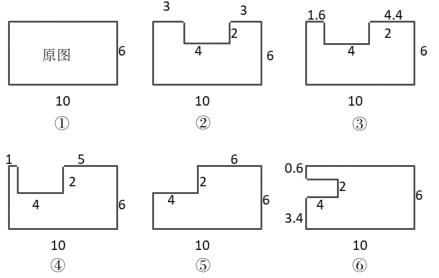
师：能求出这个长方形（如图①，单位：厘米）的周长吗？（生集体回答）如果从这个图形中去掉一块（如图②），变化以后的图形周长又是多少呢？

生1：把这个图形的各条边的长度一段一段加起来就可以算出周长了。

生2：一段一段地加太麻烦了，我们可以把4厘米的这条边向上平移，可以看出，新的图形的周长比原来长方形的周长多2个2厘米。

师：借助平移求不规则图形的周长确实方便，也能清楚地发现变化后的图形的周长与原来图形的周长之间的关系。我们现在把图形变一变（演示课件：从图②变化到图③、④、⑤、⑥），请同学们求出变化后的每个图形的周长，然后和原图比较，有什么发现？为什么？

生3：通过平移，我们可以发现图②、③、④的周长是一样的，都是在原长方形的周长上增加2个2厘米，图⑤的周长和原长方形周长相等，图⑥的周长比原长方形的周长增加了2个4厘米。

生4：都是从原长方形中去掉相同的长方形，变化之后图形的周长可能增加，也可能不变。如果从顶点去掉长方形，周长不变；如果在每条边的中间去掉长方形，利用平移的办法，剩下图形的周长与原图形的周长相比，多了两条去掉图形的长或宽。

师：大家观察得很仔细，思考问题也很全面，如果从面积的角度思考呢？

生5：无论怎样变化，图②到图⑥的形状虽然不同，但阴影部分（剩下图形）的面积是相等的，都是从原来长方形的面积中减去小长方形的面积。

师：你们真是一群会学习的孩子！能从变中找不变，很了不起！还有别的发现吗？举例说说看。

生6：周长相等的图形，面积不一定相等，如原图和图⑤。

生7：面积相等的图形，周长可能相等，如图②、③、④。

生8：面积相等的图形，周长也可能不相等，如图⑤、⑥。

生9：周长大的图形，面积不一定大，如图⑥和原图。

师：孩子们善于观察、对比、思考，发现的结论也很有价值。学习数学就是这样，在观察中思考，在思考中享受发现的乐趣！

在上面的设计里，学生于变中找不变。就是在这个思辨的过程中，学生的认识越来越接近图形的面积与周长的本质认识。

四、迁移与应用

迁移与应用指的是将所学的知识转化为新的认知或者转化为综合实践能力。深度学习离不开迁移与应用，任何脱离实际应用的学习是称不上深度学习的。可以说，应用是迁移的重要表征，也可以说，学习就是为了迁移。如果把学习活动看作一个闭环结构，那么迁移便在闭合处。它既是学习开始的端点，也是学习结束的端点，从别处迁移来，又从这里迁移到别处去。应用也是如此，既是上一个环节学习结果在此处的应用，又通过应用开启新的学习。如此，学习内容的系统性、结构性以及随着活动深化而展现的深刻性与丰富性，学生学习的主动性、积极性、自觉性都在迁移与应用中得以显现。

例如，我们在教学六年级“圆柱与圆锥的整理与复习”这一内容时，设计了下面这样一个活动。

课件出示：r=2.5cm，h=12.5cm。

师：这是一个圆柱的底面半径和高的数据，请你先比划一下这个圆柱有多大，再想象一下它可能是生活中的什么物体。

生：可能是笔桶、水杯……

师：大小相近，猜测合理。看看老师带来的是什么呢？（拿出一罐饮料）看看你们比划的，跟它差不多吗？（学生修正）

师：针对这罐饮料，你能提出什么数学问题呢？

生1：它贴的商标面积是多大？它的体积是多少？需要用多少铁皮？

师：它上面注明含有240毫升的饮料，商家有没有欺骗消费者呢？

生2：可以算出它的容积，再和240毫升比较。

（学生计算）

师：看到计算结果，你发现了什么？

生3：商家没有欺骗消费者，因为得数比240大。

师：为什么求得的数据比标明的数据还要大？

生4：可能是没装满。饮料不宜装得太满，如果装得太满，在运输途中容易发生爆炸。

师：你懂得真多！

生5：测量的有误差。

生6：我们是从外面测量的。

师：同学们猜测得合情合理。

……

在上面的学习中，迁移与应用不只是对学习结果的检验方式。迁移是经验的扩展与提升，应用是将内化了的知识外显化、操作化的过程，这也是培养学生空间观念的重要过程。

由此可见，深度学习的理论不是某一流派的理论演绎，而是历史上优秀教育理论成果及优秀教学实践经验的汇聚与提炼，是对学生学习与发展的一般道路的现实探讨。深度学习实践的理论价值，不仅仅在于克服机械学习、浅层学习的弊端，让学生学得主动、积极，更重要的是，要克服长期以来的种种二元对立，使教师、学生、教学内容（知识）获得高度的统一，使教学内容（人类历史文化、人类认识成果）发挥其应有的价值，使教师、学生在教学中获得最大发展，帮助学生形成有助于未来可持续发展的核心素养。

（执笔：王丽燕参加讨论人员：王丽燕、杨枚、邱娟、谢炤阳、邓求平、刘硕鹏、邓咏梅、童建笛）