在初中数学教学中渗透建模思想
张诗雯

摘 要:学会如何用一次函数的模型解决实际中的问题,能类比为其他相关函数模型的应用提供方向。在初中数学教学过程中,从学生的“生活现实”出发,建构数学模型的教学设计,渗透建模思想,帮助学生形成一定的建模意识和能力,具有十分重要的现实意义。
关键词:初中数学 建模思想 渗透
在昆山市教育局主办的第八届“百节优秀课”展示课活动中,来自昆山市葛江中学的周老师所执教的一节“用一次函数解决问题”(教材:苏科版八年级上册第六章第4节第1课时),给了笔者很大的触动。下面笔者将围绕其执教的课堂,谈谈自己的一些认识与思考。
一、课例概述
环节1:创设现实情境,建立模型
执教者在复习函数概念后,以现实生活为情境,询问“双十一”购物情况,并给出买鞋时的尺码表截图,引导学生研究尺码对情况:脚长x(cm)24.0、24.5、25.0、25.5、26.0……,对应的鞋码y(码)为38、39、40、41、42……
由此引发学生用数学的思维思考:这两组数量有什么关系?(函数关系)还有哪些方法来描述它们之间的函数关系?(函数表达式、画图像)有了函数表达式后,我们能解决什么问题?(只要测得脚长就能算出对应鞋码)学生经历观察、猜想、验证和归纳的过程,从而由现实问题建立了“脚长与鞋码”之间关系的数学模型:
环节2:引入现实问题,巩固模型
在学生初步感受到建模思想的重要性后,继续引入现实中购物问题,在“将鞋子加入购物车后,查询了该鞋厂的信息,其固定成本为每天1200元,生产鞋子的成本合计为每双90元”。由此执教者引导学生思考能得到哪些数学信息?这些量有什么关系?此时,呈现出具体问题,即写出成本与产量之间的函数表达式与相关销售利润问题。由此进一步巩固模型的运用,学生再次体会到数学建模在解决实际问题中的用处。
环节3:延伸现实背景,运用模型
延伸该背景并巧妙结合教材例题,“该鞋厂贴出招聘信息:应聘者被录用后第 1 年的月工资为 2 000元,在以后的一段时间内,每年的月工资比上一年的月工资增加 300元。”从而借助一次函数模型解决月工资与年份的关系问题,并由建立的模型进一步追问学生还能解决什么问题,充分体现运用模型在解决相似问题时带来的便利。
环节4:拓展现实问题,深化模型
经销商若卖出不超过50双鞋子,不予奖励;若超过50不超过100双,奖励80元;若超过100双,则超过的部分另按3元/双奖励。本环节进一步拓展问题的深度,自然引入分段函数的练习,深化模型的同时,带领学生感悟函数模型能简略很多重复计算,提高工作效率的目的。
环节5:完整现实脉络,体会模型
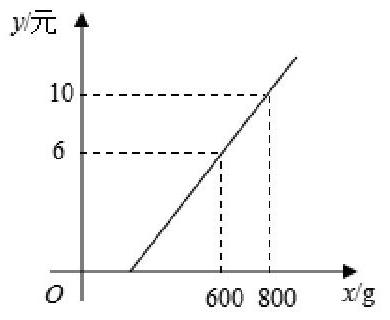
已知邮寄一定重量的包裹免收快递费,超过则需另付快递费,快递费用y(元)与重量x(g)是一次函数关系,其图像如图所示:
结合一次函数图像可利用待定系数法求出具体函数表达式,由学生发现、提出、解决问题,培养学生根据模型发现问题的慧眼。
二、分析与讨论
义务教育的数学课程能为学生在未来生活、工作和学习奠定重要的基础[1]。故而数学课程在教授中应体现“问题情境—建立数学模型—理解、应用与发展”,让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程[2]。因此,在初中数学教学中研究建构数学模型的教学设计,渗透建模思想,帮助学生形成一定的建模意识和能力,具有十分重要的现实意义。
本节课,执教者充分利用了当时的“双十一购物节”背景,通过“买鞋查询鞋码——鞋厂销售利润问题——鞋厂招聘信息——经销商奖励金额——包裹快递费”几个现实问题,在调动课堂氛围的同时,紧紧围绕一个现实主线,自然引入一次函数的数学建模,在逐步丰富情境、深化实际问题的过程中,渗透建模思想,引导学生感受建模在分析、解决实际问题中的作用。在整个教学过程中,学生在教师的引领下不仅学会,而且会学,并达到了乐于学的效果。教师以学生的最近发展区为原则,关注学生从情境中发现问题的过程,贯穿始终的问题是“你能提出什么问题?”“你能解决什么问题?”可见,执教者致力于培养学生发现、提出、分析和解决问题的能力,在无形中训练学生的探究意识和创新能力。
一次函数作为八年级学生首次接触的一类函数,同时也是后继学习反比例函数和二次函数知识的基础,学会如何用一次函数的模型解决实际中的问题,对之后的教学有很大的帮助。因而,执教者在充分钻研教材,把握重难点的基础上,结合教材上的例题设置成在“购物节”大背景下的环节2与环节3,融会贯通,不至于学生在导入环节1后便快速感知到浓重的“数学味”,而失去学习积极性。在深化模型的环节4中,执教者又合理地设置了分段函数的数学模型,拓展模型形式,展开分类讨论,把促进学生全面发展作为教学的出发点与最终归宿;环节5則是结合前一节的一次函数图像,培养学生数形结合的意识,旨在进一步突出函数模型的优势与便利。
三、感悟与启示
教学过程渗透建模思想对初中数学教师来说非常重要。教师要结合实际情况,进行更能体现数学本质、自然的、有“数学味”的创新教学设计,将培养数学核心素养落到实处,这无论是对数学学科的发展、学生个人的发展抑或是教师的专业发展都有着举足轻重的作用。
初中数学是基础教育的重要阶段,但学生做的很多应用题都与实际生活有较大的差别。因而,如何从生活背景下抽离出符合学生经验,又能与教学内容相匹配的情境,让学生真切感受到基于现实的数学问题,为孕育建模思想提供生长点,是初中数学教学发展的必然趋势。

