系泊多浮体耦合系统水动力特性数值分析

李 鸿，张斐斐，李 莉，秦 超

(1. 哈尔滨工程大学 航天与建筑工程学院，黑龙江 哈尔滨 150001；2. 哈尔滨工程大学 材料科学与化学工程学院，黑龙江 哈尔滨 150001)

0 引 言

各类码头的建成、海上运输的高速发展和我国领海海域的保护，使系泊多浮体系统得到广泛应用。针对桥梁的非通航孔设计了各类浮式防船撞设施，避免因桥墩受到船舶撞击而带来严重的人员伤亡和经济损失。在各类危险品码头也逐渐发展了浮体系泊式防撞系统，用于拦截由于恶劣环境或船舶机械故障引起的意外事故，保护码头的同时也避免了灾难性的海上污染。

沈庆[1–2]采用势流理论计算了规则波作用下的单系泊浮体受到的流体压力，使用Huston方法和Kane方程提出了用于求解多浮体系统中浮体质心位移和角位移的复数线性代数方程组。王翔[3]采用三维频域函数法得出波频和浪向对浮体的运动响应和锚缆张力产生很大的影响，且在低频范围内出现极值。王桂波[4]通过模态法研究了受到规则波作用的铰接多浮体结构频域运动响应，发现浮体的运动响应受到水深、铰接位置和波浪周期的影响。袁培银[5]对深海半潜式多浮体新型系泊系统进行了时域分析，新型设计可以在一定程度上改善平台的运动响应，满足系泊缆的安全要求，在钻井作业时保证平台的安全性。高峰[6]采用物理模型研究了多船过驳平台的系泊特性，试验得到各浮体在风浪流作用下的运动量，并测试了系泊缆张力的变化。于文太[7]使用Matlab-GUI开发的计算软件，分析了多浮筒悬链线系泊缆索姿态曲线的影响因素。王贝壳[8]提出了适用于非通航孔桥墩的防船撞拦截网装置，对比AQWA数值模拟结果与试验结果，验证了拦截网工程设计的有效性。夏雪[9]提出了小水线面浮式拦截系泊体系，结合物理模型试验和数值模拟，验证了该系统在深水海域具有更好的适应性。张周康[10–11]使用计算流体力学软件和多刚体动力学理论，通过嵌套网格方法、VOF方法对斜浪作用下的浮体系统进行了运动响应的模拟分析，对比实验结果验证了数值模拟方法的正确性。在海洋动力环境要素作用下，王鑫[12]采用物理模型试验方法，对系泊浮筒的运动响应和系泊缆的动力响应进行研究。

系泊浮筒链防撞系统为多浮体耦合结构，涉及多浮体运动响应和和系泊缆绳张力问题，具有对各种海上建筑适应性强、成本低廉、易于施工修理等特点，但是由于各浮体之间存在结构和水动力的耦合作用，运动和动力响应与单浮体系统有明显不同，对其水动力特性缺乏系统研究，这在一定程度上限制了该系统的应用。因此，本文使用AQWA软件，在物理模型试验的基础上建立系泊多浮体耦合系统的水动力模型，对不同海洋环境下的多浮体系统，采用全耦合时域分析方法，进行浮体运动响应和系泊缆绳动力响应的数值计算，得到浮体横移量和系泊缆绳张力的数值解，并与物理模型试验的结果进行对比分析。

1 多浮体耦合系统

多个浮体相互连接组成系泊多浮体系统，多浮体系统的形式多种多样，海上浮式移动平台FPSO、桩群结构以及系泊防撞系统等，本文选取系泊浮筒链式防撞系统[12]进行系泊多浮体耦合系统的全耦合时域分析。

1.1 系泊浮筒链系统模型

浮筒直径 4 m，长 18 m，质量为 80 kg，每个浮筒分布有4条系泊缆，浮筒间缆绳长5 m，浮筒链总长度为552 m，水深48 m，浮筒和缆绳的布置以及缆绳编号如图1所示。

1.2 系泊缆绳参数

图 1 系泊多浮体耦合系统布置图Fig. 1 Arrangement of mooring multi-body coupled system

采用线性缆绳，王鑫[12]在物理模型试验中采用的缆绳受力变形曲线如图2所示，使用Matlab将试验中的缆绳受力变形曲线拟合成下列函数：

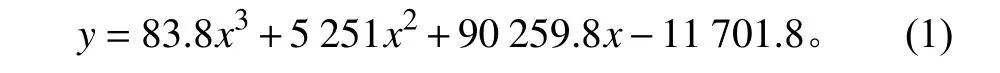
图 2 缆绳受力变形曲线Fig. 2 Force-deformation curve of cable

1.3 系泊浮筒链系统水动力模型的建立

采用AQWA软件，在物理模型试验的基础上建立系泊系统的水动力模型，如图3所示。

图 3 系泊系统水动力模型Fig. 3 The hydrodynamic model of mooring system

2 海洋环境动力要素

2.1 波浪谱

采用不规则波JONSWAP谱进行数值模拟，其表达式为[13]：

表 1 波浪要素Tab. 1 Wave parameters

2.2 海流参数

海流速度随时间变化缓慢，因此在工程设计中，为简化起见，海流被当作稳定的流动，垂线流速分布公式如下所示：

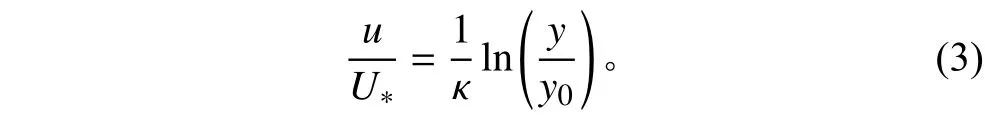
3 结果与分析

考虑单纯波浪和波流共同作用的不同海洋环境，利用AQWA软件对系泊浮筒链系统采用全耦合时域分析方法，进行浮体运动响应和系泊缆动力响应的数值计算。浮体在波浪载荷作用下，随着波浪方向发生位移响应，当波浪或水流进一步在浮体周围形成绕射水流后，浮体随着绕流的不对称性会沿着系统轴线发生蛇形摆动，浮体之间会产生相互干扰，由于系泊缆的约束作用，浮体系统的运动主要表现为横向运动，为了验证数值模拟方法的可靠性和精确度，选取物理模型的实测波要素和水流速度，采用全耦合时域分析方法对系泊多浮体耦合系统进行了数值计算。

3.1 单纯波浪作用下系统的运动响应和动力响应

对系泊缆绳施加40 kN的预张力，浮筒之间的连接缆绳不施加预张力，在不同有义波高和谱峰周期的单纯波浪作用下，全耦合时域计算时间设置为600 s。在有义波高为0.85 m的单纯波浪作用下，系泊浮筒链系统的浮体横向运动时间历程曲线如图4所示，缆绳张力时间历程曲线如图5所示。

图 4 浮筒横向运动时域曲线Fig. 4 Time domain curve of buoy lateral motion

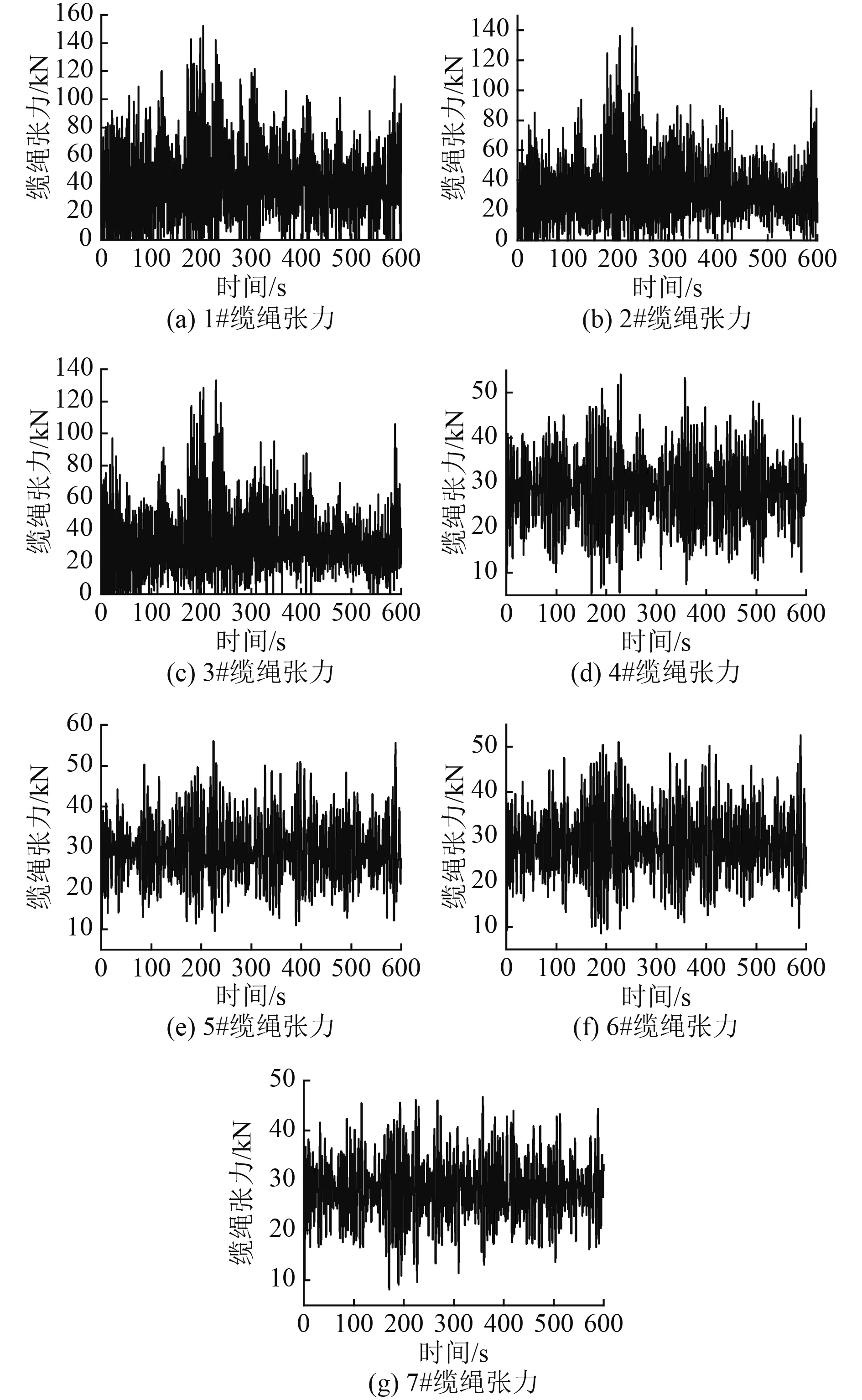
图 5 缆绳张力时域曲线Fig. 5 Time domain curve of cable tension

观察图4可知在0.85 m有义波高的单纯波浪作用下，浮筒沿着轴线做往复运动，最大横向位移出现在200 s附近，达到 1.17 m，横向位移的平均值为 0.17 m，表明浮筒基本可以回到初始位置。由图5（a）可知：浮筒前后往复运动的同时也在随着波峰和波谷上下运动，出现端部系泊缆张力小于预应力的情况，浮筒在前后往复运动时，端部系泊缆的张力随着浮筒横向运动分量的增大而增大，最大值为152.3 kN。由于浮筒链随着不对称绕流发生蛇形摆动，在端部系泊缆的约束和各浮筒之间的耦合作用下，中间浮筒的横向位移最大，导致中间浮筒两端的缆绳张力比其他浮筒间缆绳张力大，图5（b）和图5（c）描述了2号和3号缆绳张力的时域曲线，最大值分别为141.6 kN和133.3 kN。观察图5（d）～图5（g）发现：中间浮筒迎浪侧的4号和5号系泊缆张力的最大值为54 kN和56 kN，6号系泊缆的最大值为51 kN，由于浮筒链向后运动的最大位移为0.85，所以背浪侧缆绳的最大张力相对较小，为46.7 kN，在保证不走锚的情况下，要重点关注中部位置浮筒迎浪侧的系泊缆张力。结合图4和图5发现：缆绳的最大张力与最大横向位移均出现在200～250 s之间。

不同波浪作用下浮筒横移量的试验和数值模拟结果见表2，试验和数值模拟得到的系泊缆张力见表3。

分析可知：采用全耦合时域分析模拟得到的浮筒横向运动分量的最大值与模型试验得到的结果较为接近，浮筒间缆绳张力的试验值和模拟值也普遍较为接近。物理试验中安装了21个浮筒，为了节省计算时间，水动力模型只选取了中间位置的7个浮筒，通过增大端部系泊缆的长度代替减少的浮筒数量，从而使水动力模型和物理试验模型的跨度保持一致，这也导致水动力模型系统的稳定性降低。全耦合时域分析得到的背浪方向浮筒横向运动分量的平均值普遍大于模型试验的平均值，这是由于水动力模型系统的稳定性没有物理模型试验的稳定性好，导致逃逸波浪和50年重现期波浪作用时背浪方向浮筒位移最大值时域分析与试验结果相差较大，迎浪侧5号缆绳张力时域分析最大值与试验最大值也相差较大。

3.2 波流共同作用下系统的运动响应和动力响应

考虑到允许工程船舶作业的海洋环境，且当地海流流速不会超过1.2 m/s[12]，因此只考虑1.2 m/s的海流和2种作业波浪的共同作用下，对系泊浮筒链进行600 s的全耦合时域计算，系泊浮筒链系统的浮体横向运动时间历程曲线如图6所示，浮筒横向运动分量最大值的实验和模拟对比如表4所示，在50年重现期波浪的作用下，缆绳张力最大值的实验和模拟对比如表5所示。

观察图6可知：在波浪和水流的耦合作用下，浮筒发生前后摆动，在水流的冲击作用下沿水流前进方向运动量较大，而且不能回到初始位置；结合表4得到，浮筒横向位移的全耦合时域分析最大值与模型试验最大值较为接近，可以较为准确的模拟出浮筒在波流共同作用时横向位移的最大值，但是数值计算最小值和平均值大于物理模型试验平均值，这是由于水动力模型系统的稳定性没有物理模型试验的稳定性好，导致数值计算高估了系统横向运动分量的最小值和平均值。表5给出了系泊浮筒最大缆绳张力的汇总，出现在50年重现期波浪和1.2 m/s的海流同时作用下，依然是端部缆绳的张力最大，为755.6 kN，可以为锚固块体重量的设计提供参考依据。

4 结 语

本文采用全耦合时域分析方法，通过AQWA软件对浮筒链式系泊多浮体耦合系统进行了运动和动力响应数值模拟，并与现有物理模型试验进行了对比分析，得到下列结论：

表 2 单纯波浪作用下，中间浮筒横向运动分量最大值的试验和模拟对比Tab. 2 Experimental and simulation comparisons of the maximum lateral motion component of middle buoy (only wave)

表 3 单纯波浪作用下，缆绳张力最大值的试验和模拟对比Tab. 3 Experimental and simulation comparisons of the maximum tension of cable (only wave)

图 6 波流共同作用下，浮筒横向运动时域曲线Fig. 6 Time domain curve of buoy lateral motion(wave+1.2 m/s current)

表 4 波流共同作用下，浮筒横向运动分量最大值的的实验和模拟对比Tab. 4 Experimental and simulation comparisons of the maximum lateral motion component of middle buoy(wave+1.2 m/s current)

表 5 波流共同作用下，缆绳张力最大值的实验和模拟对比Tab. 5 Experimental and simulation comparisons of the maximum tension of cable (wave+1.2 m/s current)

1）在给定海洋动力要素的情况下，浮体横向位移的全耦合时域分析结果与模型试验结果较为接近，浮筒间缆绳张力的试验值和模拟值普遍较为接近。

2）由于水动力模型系统的稳定性没有物理模型试验的稳定性好，导致数值计算高估系统横向运动分量的最小值和平均值。

3）通过全耦合时域分析结果与物理模型试验结果的对比，分析了影响数值模拟结果与物理模型试验结果产生误差的原因，验证了全耦合时域分析方法的正确性，对系泊多浮体耦合系统的运动和动力响应的计算具有较好的精确度。