基于CFD的船舶双螺旋桨水动力性能分析

孔金平，吴波涛，孔令志

(中国卫星海上测控部，江苏 江阴 214431)

0 引 言

近年来，越来越多的船舶采用双主机推进，双主机推进可以增强操纵的灵活性和机动性，同时推进效率、使用寿命和经济性也得到提高。双主机推进时，2个螺旋桨之间存在一定的干扰和相互作用，因此有必要对双螺旋桨的水动力性能进行研究。CFD方法是目前普遍采用的数值计算方法，已经逐步取代部分模型试验用于船舶水动力性能的预报。CFD方法不仅花费低、时间短，而且可视化效果好，在节约成本、提供效率方面有明显优势。本文采用目前国际上比较流行的商用网格划分软件ICEM，建立了某型船舶双螺旋桨系统的三维网格模型，通过商用CFD计算软件Fluent，应用滑动网格技术，对双螺旋桨系统进行了数值计算。选取2种常用的湍流模型和，分别预报螺旋桨的水动力性能，并进行对比分析。

1 数学模型

计算流体动力学（Computational Fluid Dynamics，CFD）是数值计算方法和计算机科学结合的产物。以计算机为工具，采用离散化的数学方法，对流体的流动包括压力、速度和能量等相关物理量进行数值模拟和分析研究，以解决各类实际问题。船舶CFD是随着计算机的高速发展，与船舶流体力学相结合的产物。船舶CFD的应用大大缩短了船舶的设计周期，节约了设计费用，因此得到了普遍认可。CFD的基本思路是把原来在时间和空间上连续的物理量，如速度、压力和温度等，用一组有限个离散点上的变量值的集合来代替，并且建立离散点变量之间关系的代数方程组，通过求解代数方程组获得变量的近似值[1–2]。

1.1 控制模型

CFD的基本方程有质量守恒方程、动量方程和能量方程，分为积分形式和微分形式2种。积分形式是流体各种物理量之间的积分关系式，求解积分形式基本方程可以得到总体性能关系，如流体与物体之间的总作用力和总能量交换等。微分形式是流体各种物理量之间的微分关系式，求解微分形式基本方程可以得到流场内部的一些细节，包括各网格点上流体的速度、压力和温度等。

1）质量守恒方程

对于一个控制体来说，单位时间内流入控制体的质量等于控制体内质量的增加量，因此有平衡关系式[4]：

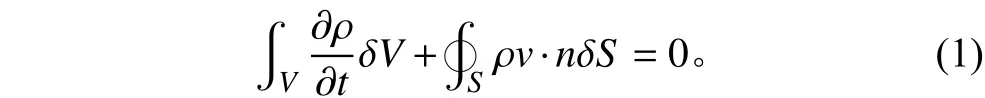
2）动量方程

根据动量定律，微分型动量方程[4]：

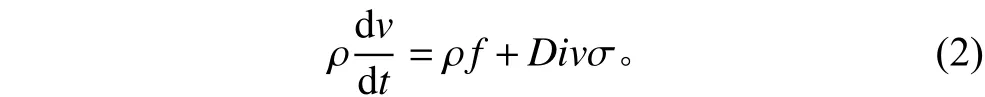
3）能量方程

假设流体外界的能量交换只限于机械能和热能，在有其他能量交换时可加入相应项，微分型能量方程[4]：

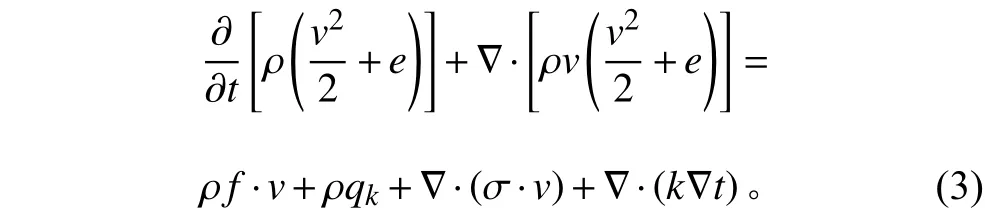
以上所列质量守恒方程、动量守恒方程和能量守恒方程不封闭，还需要增加附加条件。对于牛顿流体来说，速度、压力等物理量的关系都是线性的，具体形式可表示为：

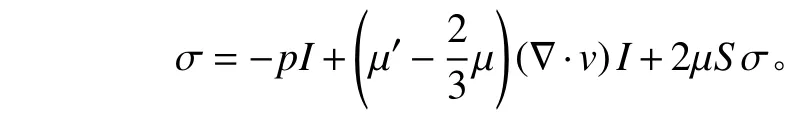
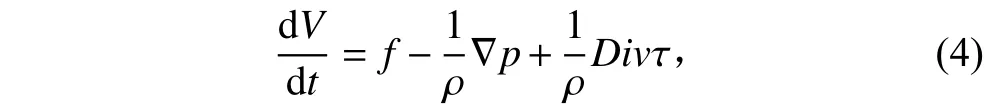
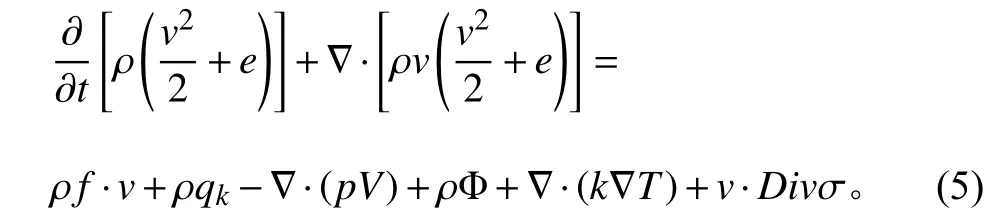
式(4)和式(5)与式(1)一起构成了牛顿流体流动的基本方程，称为 N-S 方程[3–4]。

1.2 湍流模型

工程中遇到的流体流动一般都是湍流。湍流是不规则的、多尺度的、非定常的流动，有很强的扩散性和耗散性。N-S方程能够准确地描述湍流运动的细节，但求解这么复杂的方程需要非常强大的计算机和耗费大量的时间。因此，工程计算中均采用湍流模型来简化计算。湍流模型的选取一般根据流体是否可压、计算精度要求、计算机性能和计算时间等因素。本文所涉及的模型中包含了外场均匀来流和螺旋桨的复杂旋转流动，螺旋桨之后的漩涡流动占了很重的比例，因此选择合适的湍流模型将至关重要。本文将对和两种不同湍流模型进行计算比对。

1.3 滑动网格

在Fluent中转子和定子之间的相互作用问题不能简单的通过把坐标系转换成旋转坐标系来解决，两者之间的相互作用必须通过MRF方法、混合平面法或滑动网格方法来解决，本文采用滑动网格[5–6]方法来处理旋转部件位置上的网格。使用滑动网格技术时，将计算域划分为不同的流动区域，相邻的流动区域由交界面分开，并沿着交界面相互滑动。计算过程中，每迭代一步，网格的位置进行重新计算，并重新确定网格点在交界面上的相对位置，并进行通量的传递。

2 计算模型

CFD计算工具采用主流分析软件Fluent，流体介质为水，螺旋桨区域采用相对运动的网格边界。根据模型特点，CFD计算采用边界条件类型包含：速度进口、对称面、壁面、interface、远场边界等。受螺旋桨限制，速度进口均采用来流速度为14 kn（即7.196 m/s），远场即为自由出流边界。

模型的网格采用专业网格划分软件ICEM进行划分。由于在交界面上的网格是非正则的，即交界面两侧区域的网格不一样，因此交界面上的信息采用插值计算进行相互传递。网格计算域内存在2个子域，分别为旋转域与静止域。此2种子域的网格进行单独划分，采用交界面interface进行整体网格接合后，再进行数值计算。

船舶长度为222.2 m，型宽为25 m，排水量为25 000 t，设计吃水8 m，设计航速14 kn。螺旋桨叶数为5，螺旋桨直径5.5 m，2个螺旋桨间距为7.6 m，设计转速为127 r/min。

由于螺旋桨的扭转角较大，对网格划分造成一定的难度，需要进行较为复杂的拓扑构造与网格调整，才能保证网格疏密均匀、网格量合理、网格质量高的要求。计算模型远场为直径33.2 m、长43.2 m的圆柱体，静止域与运动域的交界面为直径6.624 m、长1.6 m的圆柱。网格划分的主要过程为建立不同模型的拓扑结构，壁面附面层加密，螺旋桨周围网格重点加密，并对网格进行疏密过渡。计算模型的网格均为结构化网格，网格示意如图1所示，网格量约为190万。

图 1 模型网格示意Fig. 1 Model grid schematic

3 数值分析

3.1 收敛判据

CFD数值计算时边界条件的设置主要有速度进口边界条件、对称面边界条件、壁面边界条件、interface边界条件和边界条件，其中远场的边界条件主要根据来流情况设置。对模型的CFD计算过程都较为顺畅，5 000步左右趋于收敛，如图2所示。最后残差收敛到10–5以下，管道进出口流量差小于0.5%，这样可以判定结果已收敛完全。

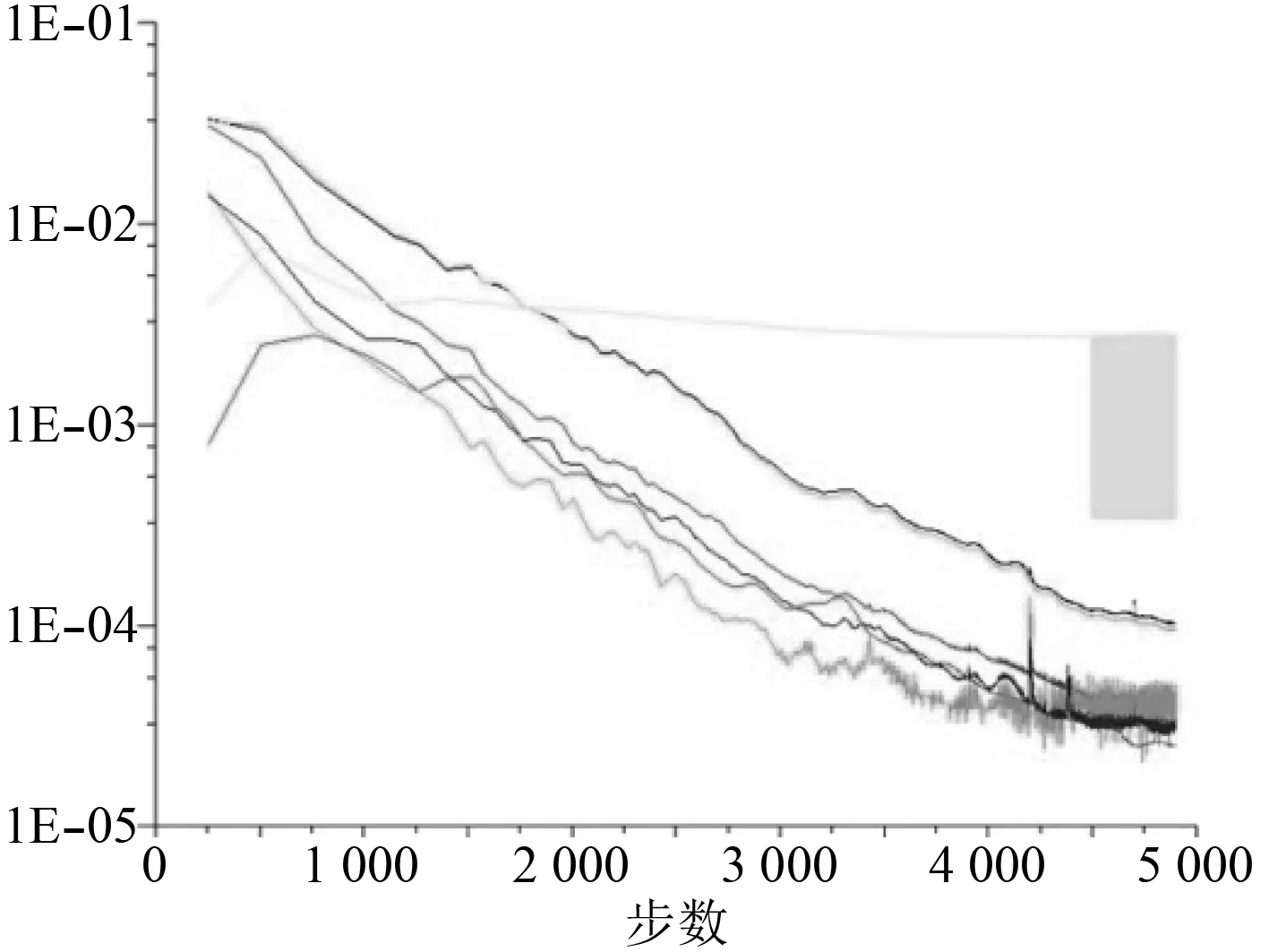
图 2 残差曲线示意图Fig. 2 Schematic diagram of residual curve

3.2 不同湍流模型数值分析

针对螺旋桨性能进行分析，因此流场截面选择了螺旋桨的前后及中分面，如图3所示，3个截面的位置分别为y=0，z=92.2 m及z=93.5 m。通过该3个截面及所有壁面数据导出压力、速度数据，即可处理得到相应的流场图片。

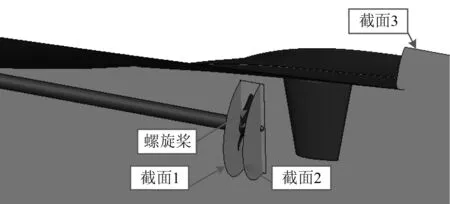
图 3 流场剖面示意图Fig. 3 Schematic diagram of Flow profile

通过不同湍流模型CFD计算，验证湍流模型对计算结果的影响。双方程k–ε及k–ω模型流场对比如图4~图6所示。通过螺旋桨周向的3处截面的速度分布对比，受到螺旋桨压缩影响，桨后水流速度均有所加快，螺旋桨旋转过程中形成了有效推力。但仅通过速度对比，2种湍流模型差别并不明显。

通过计算数据统计，获得2个湍流模型下的推力及扭矩数值，通过公式计算出螺旋桨效率，如表1所示。通过对比，湍流模型的螺旋桨效率偏低一些，模型的螺旋桨效率比模型的螺旋桨效率高5%，由此可判断不同湍流模型略有差别。

3.3 双螺旋桨数值分析

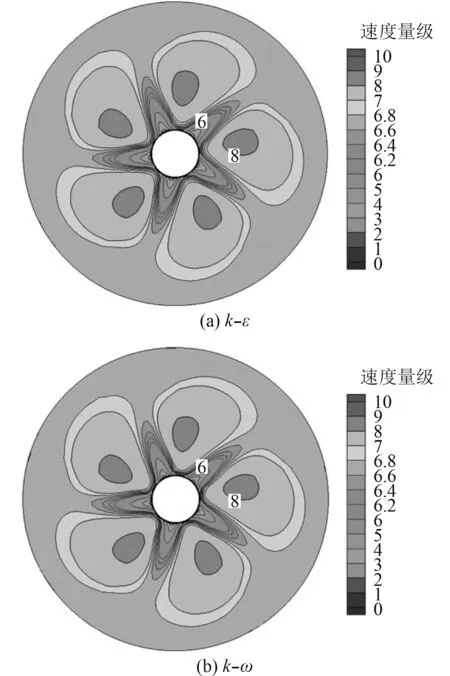
图 4 截面1速度场分布Fig. 4 Velocity field distribution of section 1

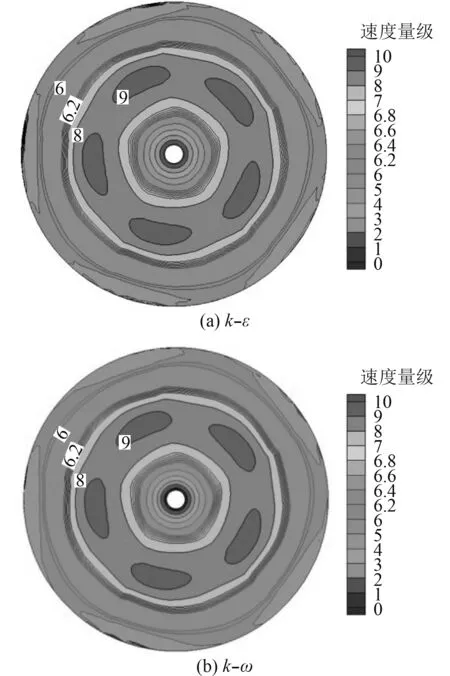
图 5 截面2速度场分布Fig. 5 Velocity field distribution of section 2

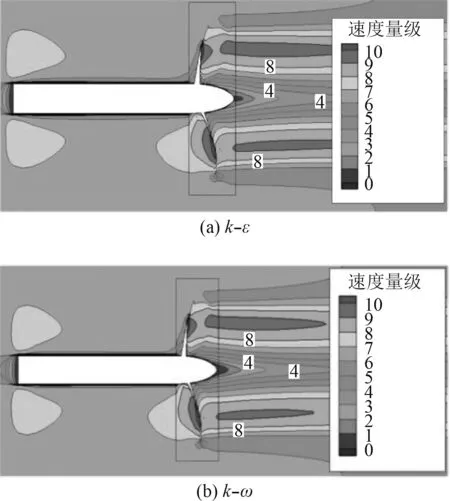
图 6 截面3速度场分布Fig. 6 Velocity field distribution of section 3

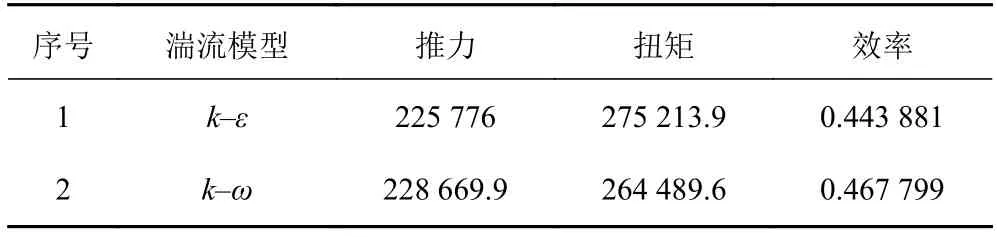
表 1 不同湍流模型螺旋桨效率Tab. 1 Propeller's efficiency of different turbulence model

考虑到研究对象为对称双螺旋桨，通过非对称单独完整模型和对称边界模型进行CFD数值分析，得到流场如图7~图9所示。从流场图上观察，非对称计算结果与对称计算结果的速度场在截面1和截面2处几乎没有区别，在截面3处非对称计算结果中，高速区域相对更多，但分布情况基本相同，因此，2个螺旋桨之间没有相互干扰。

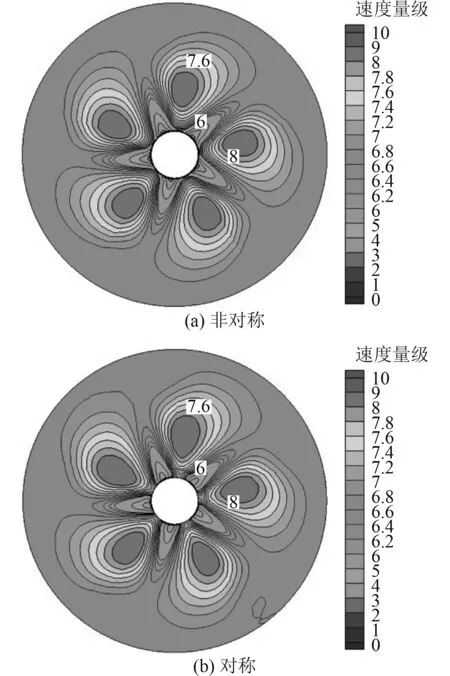
图 7 截面1速度场分布Fig. 7 Velocity field distribution of section 1

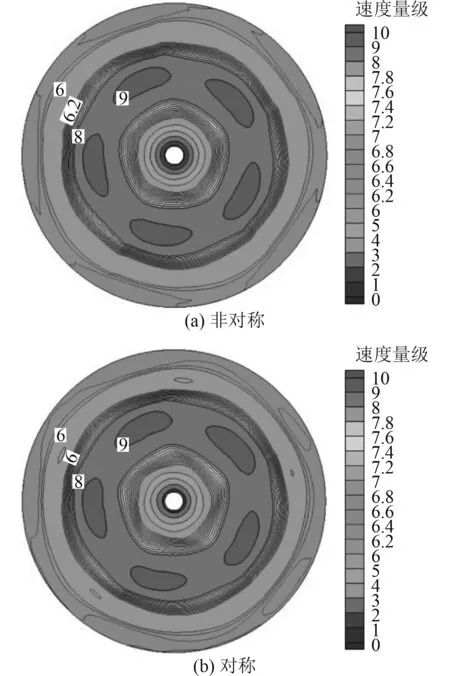
图 8 截面2速度场分布Fig. 8 Velocity field distribution of section 2

通过螺旋桨效率分析，如表2所示。对称情况下双螺旋桨的推理力和扭矩都有所下降，但是效率相比于不对称情况提升了1.4%。

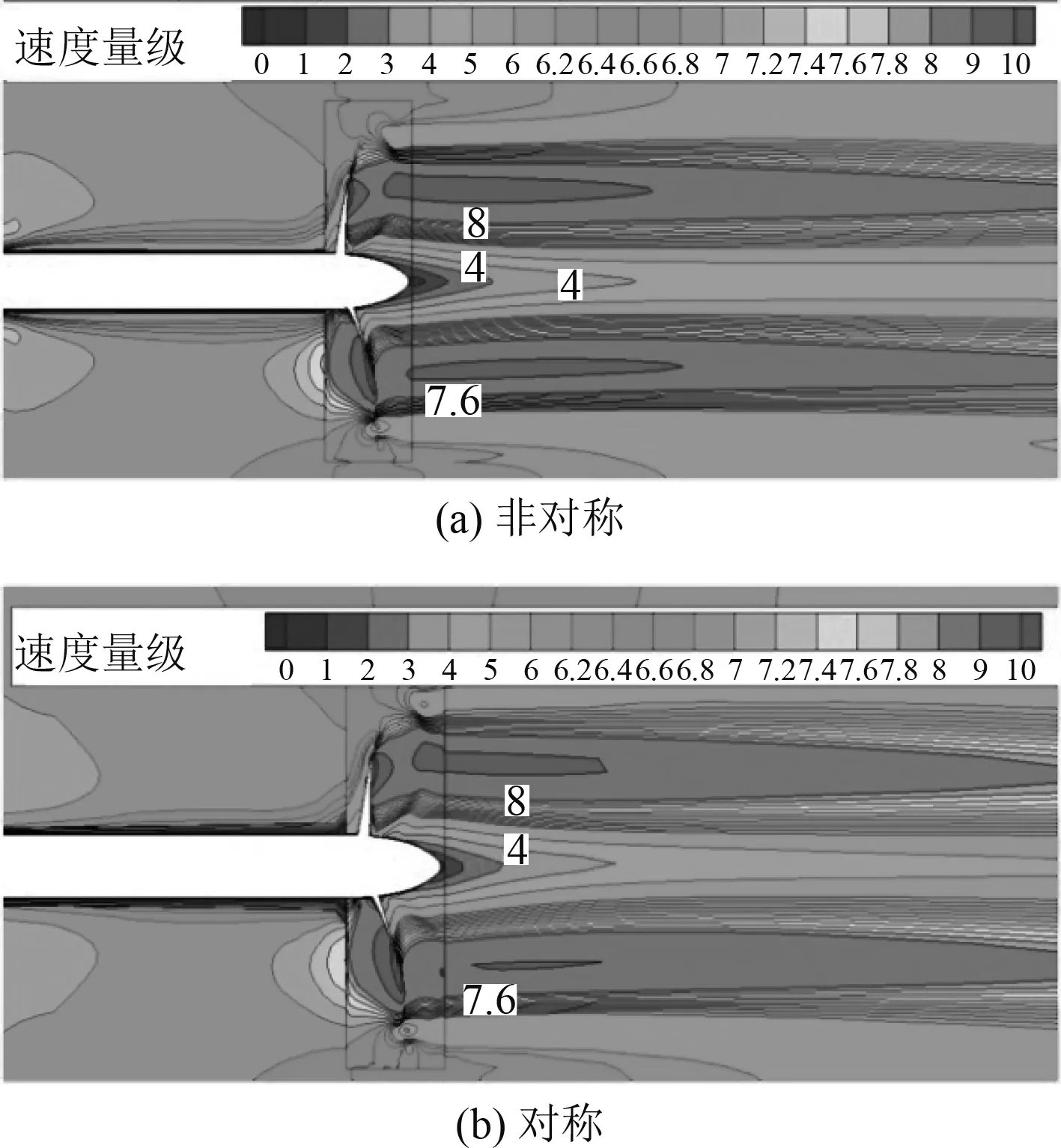
图 9 截面3速度场分布Fig. 9 Velocity field distribution of section 3

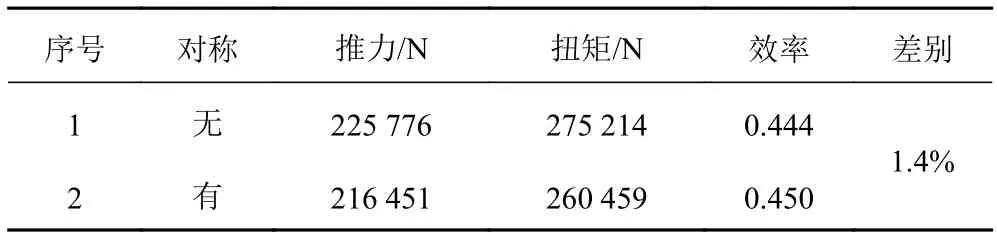
表 2 双螺旋桨效率Tab. 2 Dual-propeller's efficiency

4 结 语