WFAR模型在时间序列预测中的应用

王立柱, 孟宪涛

(沈阳师范大学 数学与系统科学学院, 沈阳 110034 )

0 引 言

近10年,关于时间序列预测的研究成果从建立模型的角度主要包括3个方面:1)基于线性模型的预测;2)基于非线性模型的预测;3)基于模糊集合理论的预测。经典的ARIMA模型由于其良好的统计性质及著名的Box-Jenkins方法得到了广泛应用[1],但受到假定时间序列具有线性相关结构及较多的时间序列观测值才能确保获得理想预测结果的限制。在大数据背景下,复杂的时间序列数据往往伴有非线性结构,此时建立线性模型已不再适合。基于非线性模型的预测主要是将一些人工智能方法用于时间序列预测,如传统的机器学习方法包括人工神经网络[2-3]、信息颗粒[4-5]、贝叶斯网络[6]、支持向量机[7]等,以及各种深度学习算法,形成一些非线性模型。很多文献提出用人工神经网络ANN(Artificial Neural Networks)对时间序列建立非线性模型的方法进行预测[8-9]。由于人为或设备故障等原因,可能会产生缺失或奇异数据等现象。模糊时间序列模型更适合解决观测数据带有缺失、含糊、不准确等现象的预测问题,且不需要大量的历史数据。1993年,Song和Chissom[10]第一次提出了模糊时间序列模型,之后被广泛地应用于金融、水文、生物等领域。

采用模糊时间序列模型进行预测的过程主要有如下4个步骤:划分论域、数据模糊化、建立模糊规则、预测。模糊时间序列预测的研究成果主要集中在如何划分论域及如何建立模糊规则,其原因是这2个步骤直接影响预测质量。划分论域方面,最初采用均匀划分。随着研究的深入,提出了非均匀划分,包括根据数据的分布进行论域划分、考虑时间因素的论域划分以及考虑了异常值的论域划分等[11]。建立模糊规则方面,最初采取朴素的根据模糊逻辑关系确定模糊规则的方法,之后又出现了二型、高阶及加权模糊规则等[12-13]。还有学者提出用非线性函数代替建立模糊规则进行直接预测,最典型的是利用神经网络建立模糊规则直接预测。建立模糊规则方面,已有的文献多数都只是简单地对模糊规则进行加权平均,即只简单地考虑观测数据状态波动的频率。而现实时间序列数据状态波动受到诸多外在因素的影响,这些影响又是错综复杂的,很难用结构式的因果模型诠释。数据状态波动的依赖关系应是问题研究最重要和最有用的特性。

基于上述分析,本文提出的模糊时间序列模型,既考虑了数据状态间的相互影响关系,又兼顾了状态转移频率的影响。将TAIEX1995数据作为实验数据,实验结果表明模糊集合理论对预测质量起到了良好作用,其预测质量明显优于传统预测模型。

1 基础知识

1.1 马氏性检验

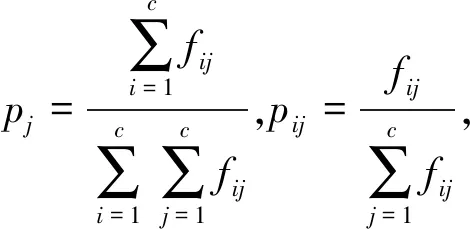
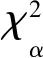
1.2 FCM模糊聚类

Fuzzy C-Means(FCM) 是由Bezdek于1981年提出的一种模糊聚类算法,是目前应用最广泛且较成功的一种算法。它通过优化目标函数得到第j个样本点xj到第i类中心vi的隶属度aij,从而决定样本点的类属以达到自动对样本数据进行分类的目的。目标函数如下:

其中:β>1为模糊化权重系数;n为数据样本容量;c为聚类中心数量;d(xj,vi)表示样本点xj到聚类中心vi的距离;aij是相应的隶属度。

Fuzzy C-Means(FCM) 算法是一个迭代优化过程,按照下式对聚类中心及隶属度进行更新,直到满足终止条件。

本文中β=2,终止条件为迭代次数达到1 000次或相邻2次目标函数值相差不足1×10-5。

2 WFAR预测模型

模糊时间序列模型广泛应用于数据预测分析领域,其优势在于能够完成对具有不完整性、不准确性和含糊性等缺点的数据的预测。在建立模糊规则方面,已有的文献多数都只是简单地通过模糊关系出现的频率建立模糊规则,由于随机性的存在,单纯的从出现频率考虑问题,很难准确反映事实。在此重点考虑了模糊状态间的相互影响关系及影响程度,又兼顾了状态转移概率的影响。提出了加权模糊自回归(WFAR)模型。

首先,利用模糊聚类将时间序列观测数据划分成c个模糊状态Ai(i=1,2,…,c)。其次,通过自相关系数确定相互影响关系程度。最后,采用加权平均实现最终状态预测。

上述是WFAR预测模型总体框架,具体构建模型步骤如下:

1) 利用FCM模糊聚类方法确定时间序列在各时刻的模糊状态。

2) 对时间序列序列进行马氏性检验。

3) 计算t-i时刻状态Ft-i对t时刻状态Ft的相关性影响权重ωi(i=1,2,…,p)。

首先,计算时间序列各阶自相关系数ri(i=1,2,…,p),

(1)

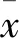
(2)

4) 通过计算滞时马尔可夫转移频率矩阵Pki(Ft-k)(k=1,2,…,p),得到t时刻状态Ai的概率Wt(i)。

计算不同滞时的马尔可夫链的转移频率P1i(Ft-1),P2i(Ft-2),…,Ppi(Ft-p)。其中,Pki(Ft-k)(k=1,2,…,p)表示t-k时刻的状态Ft-k经过k步滞时转移到第i种状态Ai的频率。它决定了时间序列在t时刻为状态Ai的概率Wt(i),即对时间序列模糊状态的转移过程进行预测的概率法则。

Wt(i)=ω1P1i(Ft-1)+…+ωpPpi(Ft-p),(i=1,2,…,c)

其中:p表示相关性阶数;c表示状态空间的基数;Wt(i)表示t时刻出现第i种状态的可能性。

5) 预测t时刻状态Ft及预测值ft。

(3)

其中:Ai表示第i种模糊状态;vi表示第i类中心。

3 实验及结果分析

以Alabama大学1971—1992年入学人数为例,以说明WFAR模型预测的具体应用。表1第2列给出了Alabama大学1971—1992年入学人数数据。

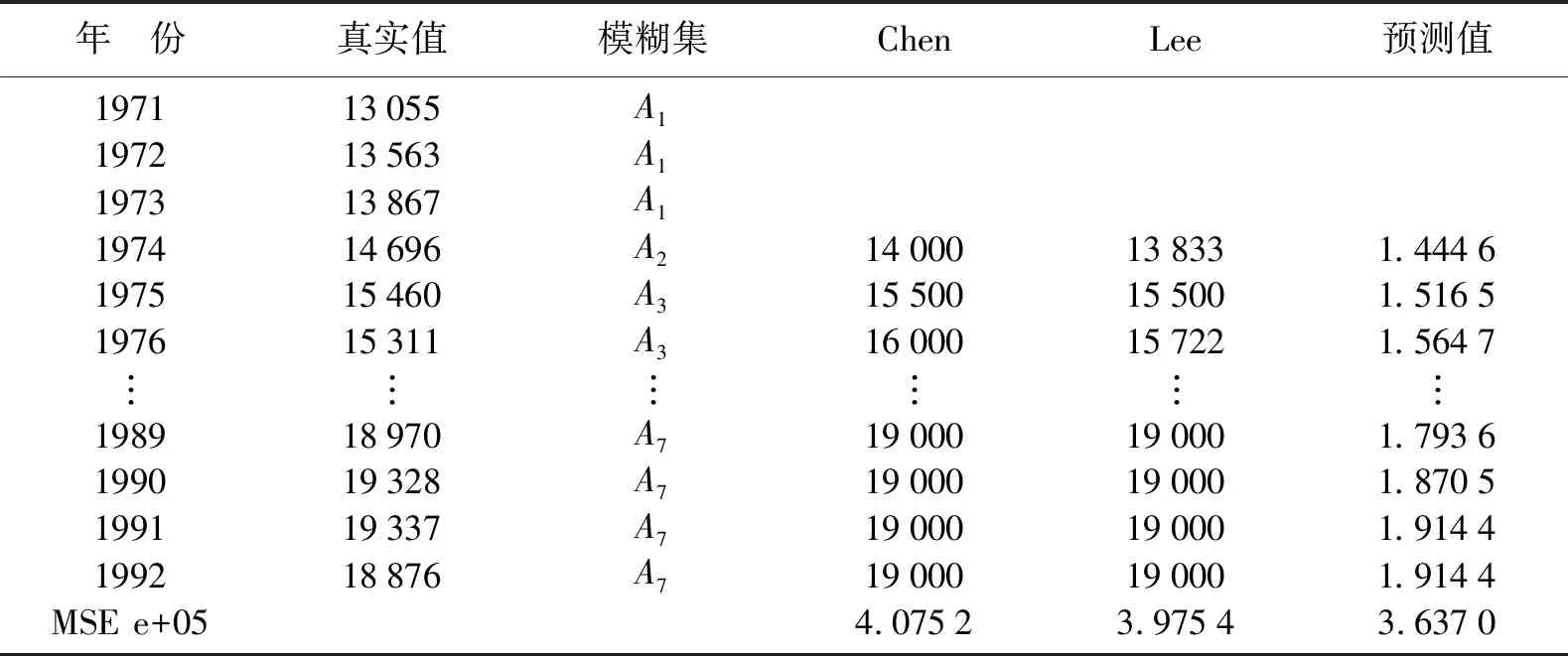
表1 模型的模糊规则及预测结果Tab.1 Fuzzy rules and performances of proposed model

1) 将时间序列数据进行模糊聚类,以确定模糊状态

为便于同其他方法进行比较,应用FCM方法将数据聚成7类,得到聚类中心vi分别为1.348 1、1.500 7、1.545 6、1.596 5、1.683 8、1.816 2、1.914 4及每年入学人数的相应隶属度,进而可以确定其模糊状态列于表1第3列。

2) 马氏性检验

经检验实验数据具有马氏性,可以使用马尔科夫链的相关理论进行预测分析。

3) 计算相关性影响权重ωi

根据公式(1)、(2)前5阶自相关系数分别为0.818 2、0.571 2、0.301 9、0.081 1、-0.060 0。由于过去3个滞时对当前状态影响较大,因此,取前3阶归一化自相关系数作为相关性权重ωi,分别为0.483 8、0.337 7、0.178 5。

4) 计算滞时转移频率矩阵Pki(Ft-k)

针对1971、1972、1973年数据预测1974年数据,得到Wt(i)(i=1,2,…,c)分别为0.429 7、0.329 2、0.228 7、0、0、0、0。

5) 预测t时刻值ft

由公式(3)计算t时刻值的预测值ft,由上一步可以得到1974年入学人数的预测值为14 446。

预测值与1974年真实数据较为接近,说明预测效果较好。以此类推,可以预测以后各个年份的入学人数列于表1第6列。传统的Chen、Lee模型预测值列于表1第4、5列。为说明预测效果,以均方误差(MSE)为标准。WFAR模型预测的MSE为3.637 0,而传统的Chen、Lee模型预测的MSE分别为4.075 2、3.975 4。实验结果表明该模型的有效性及可行性。

4 结 语

本文提出了一种一般化结构预测模型。该模型不仅考虑了状态转移频率的影响,更重要的是考虑了数据状态间的相互作用关系。实验结果表明该方法有效可行。该模型中使用FCM模糊聚类方法,也可采用一些人工智能方法更加精细划分论域得到聚类中心。在考虑数据状态间的作用关系时,也可采用更加适合的方法。进而得到更高质量的预测结果。