周期和波高对斜坡式防波堤透浪特性影响试验研究

杨会利，杨艳静，戈龙仔，谭忠华

(1.交通运输部天津水运工程科学研究所 港口水工建筑技术国家工程实验室 工程泥沙交通行业重点实验室，天津 300456；2.中交第一航务工程勘察设计院有限公司，天津 300222)

引言

斜坡式防波堤通常由堤心石、护面块体等材料组成，在海岸工程中应用广泛，但是由于斜坡式防波堤堤内块石孔隙较大，波浪容易透过防波堤堤身传播至港内侧，产生堤后次生波，影响港内泊稳条件，尤其在有较长周期波浪的地区，由于长周期穿透性强，且在港内反复振荡极不易消减，因此对港内波况和船舶泊稳有非常大的影响。目前，国内外关于防波堤堤心石在波浪作用下的运动和动力特性研究并不是很多，主要是对堤心石内波浪衰减规律[1]、波动压强分布[2]以及模型试验比尺效应[3-4]等方面进行一定的研究[5]。针对斜坡式防波堤的透浪性有很多研究，但针对不越浪情况还较少，目前国内外已有关于规则波和不规则波作用下(不考虑越浪情况)斜坡堤透浪系数主要经验公式有：斯蒂芬森[6]和习和忠[1]通过理论分析分别推导的透浪计算公式，Ahrens[7]、王登婷[8]、葛晓丹[9]和冯卫兵[5]等分别通过物理模型试验拟合得到的透浪计算公式，但只有Ahrens[7]和葛晓丹[9]的公式涉及了不规则波作用情况，而实际波浪则为不规则波，因此对于长周期波浪不规则波浪条件下斜坡式可渗透性防波堤的透浪特性进行研究，具有重要的工程意义[10]。

印尼Cilacap防波堤直面印度洋开敞海域长周期涌浪影响，本文结合印度尼西亚Cilacap电厂工程防波堤断面分别在规则波和不规则波情况下进行了周期和波高对防波堤透浪性的影响，总结了周期和波高对防波堤透浪性的影响规律，并分别拟合出规则波和不规则波情况下，斜波堤透浪系数公式，为工程设计提供科学依据。

1 模型试验

1.1 模型概况[11]

拟建防波堤工程位于芝拉扎地区，采用抛石斜坡式结构。防波堤设计断面如图1所示。考虑到本海区受长周期的影响，为研究波浪对港内波况及泊稳条件的影响，选择一定级配的堤心石在设计低水位和设计高水位条件下，采用固定波高，不同周期下以及固定周期改变入射波高分别采用规则波、不规则波测定防波堤断面的透浪系数。

1.2 试验条件

(1)试验水位：设计低水位+0.42 m；设计高水位：+2.46 m。

(2)波浪条件：以堤顶不越浪为原则，采用固定波高为H=2.0 m，不同周期下(T=8 s、10 s、13.83 s、15 s)以及固定周期T=13.83 s(断面位置处T)，改变入射波高(H=1.5 m、2.0 m、2.5 m、3.0 m)，分别采用规则波、不规则波测定防波堤断面的透浪系数。本文中规则波波高统一为平均波高和平均周期，不规则波高为有效波高和有效周期，文中规则波和不规则波作用下的相同试验条件是指规则波的平均波高、平均周期与不规则波的有效波高、有效周期一致。

(3)断面结构：断面结构如图1所示，采用抛石斜坡式结构，海侧由抛石棱体以上至内侧高程范围内均采用15 t双联块体护面，坡度为1:1.5，护面块体不规则摆放；堤内、外侧护底均采用500～700 kg块石；在外侧护底块石与护面块体之间采用抛填1 000～1 500 kg棱体块石，在内侧+3.5 m高程位置设有一混凝土挡块平台，平台以下采用700～1 000 kg块石进行护面，坡度为1:1.5。

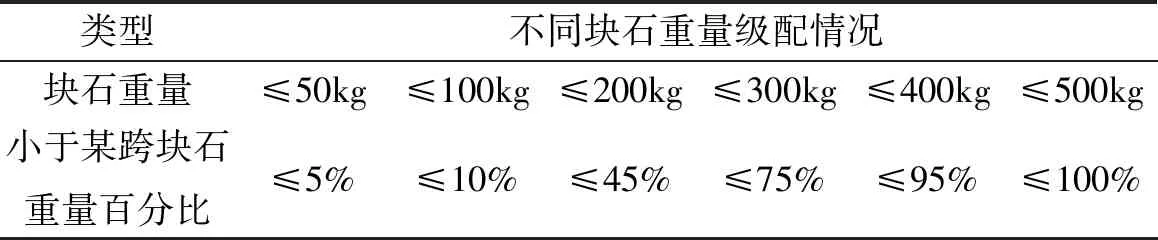
表1 堤心石各种块石的含量Tab.1 Content of various blocks of core stone

(4)堤心石选择：考虑到现场的实际情况，模型试验中参考以往在不同堤心石级配情况下透浪系数的研究成果:“堤心石在质量范围和中值粒径相同的情况下，不均匀系数所造成的堤心石级配不同对透浪系数的影响不大[5]”，因此对于1～500 kg堤心石，模型上选用的级配见表1。根据上述级配表，按不同比例和重量挑选堤心石，绘制了累积频率曲线，具体见图2。

图1 防波堤设计断面结构详图Fig.1 Details of design cross-section

图2 堤心石累积频率曲线Fig.2 Cumulative frequency curve of core stone

(5)比尺选择：根据试验设备及场地等条件的限制，根据重力相似准则模型选用几何比尺λ=33.5。对于堤心石来讲当几何比尺取得太大时,存在粘滞力的影响,水流通过堤心呈层流状态,而原型情况则往往与之相反呈紊流状态,此时模型的堤身渗透系数减小,而反射增大。为了克服这一影响,合适的办法是将按模型几何长度比尺，计算得到的堤心石尺寸按下式增大

(1)

式中：L为几何正态模型特征长度；D为块石线性长度；k为大于1的系数。

对于k值的推求，Le Mehaute提出了诺模图方法；而Keulegan通过对粒径相近的块石进行试验，给出了一个经验关系，以此求值。但是这两种方法的计算结果是有差别的，Hudson建议一般取二者的平均值。

按照Le Mehaute方法和Keulegan方法分别计算得到k值为1.30和1.73，取两者平均值为1.52，因此计算得到堤心石比尺为1:22。

(6)透浪系数测定方法：

透浪系数即为透射波高对于入射波高的比值，计算式如下

Kt=Ht/Hi

(2)

式中：Kt为透浪系数；Hi为入射波高；Ht为透射波高。

试验在波浪水槽中进行，采用电机伺服驱动推板吸收式造波机在波浪水槽内进行物理模型模拟试验，波高采用波高传感器，并通过SG2000型动态水位测量系统对波高进行采集分析，为了测量防波堤内侧透射波高，在后方布置4个测点，1#测点布置在内侧护面块石坡脚处，测点布置见图3所示，模型布置如图4所示。

图3 堤后波高测点布置图Fig.3 Measured point of secondary wave layout图4 断面模型摆放情况Fig.4 Model placement

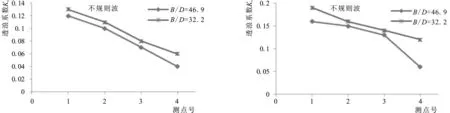
5-a H=2.0 m,T=8 s5-b H=2.0 m,T=13.83 s图5 不规则波作用下堤后透浪系数随相对宽度的变化Fig.5 Influence of relative width on the wave transmission of irregular wave

6-a H=2.0 m,T=8 s6-b H=2.0 m,T=13.83 s图6 规则波作用下堤后透浪系数随相对宽度的变化Fig.6 Influence of relative width on the wave transmission of regular wave

2 试验结果及分析

2.1 相对宽度对透浪系数的影响

图5和图6分别给出了在不规则波和规则波作用下，两种不同入射波条件下堤后透浪系数随相对宽度B/D的变化，B为静水面处的堤身宽度，D为粒径曲线上小于该粒径块石重量占总重量10%的粒径值。从图中可以看出，四个测点位置透浪系数随相对宽度的变化规律一致，透浪系数随着相对宽度的增大而减小，在相同的的波浪条件下，规则波时相对宽度的影响比不规则波时影响更明显。

2.2 透浪系数随相对波长的变化规律

图7给出了设计低水位和设计高水位波高H=2.0 m时，1#测点位置堤后透浪系数随相对波长B/L的变化，B为静水面处的堤身宽度，L为入射波波长。从图中可以看出，随着相对波长的增大，两种水位情况下，无论规则波还是不规则波作用下透浪系数随着相对波长的增大而减小，且变化比较明显，相对波长对透浪系数的影响较为敏感。

7-a 设计低水位7-b 设计高水位图7 堤后透浪系数随相对波长的变化(H=2.0 m)Fig.7 Influence of relative wave length on the wave transmission (H=2.0 m)

8-a 设计低水位8-b 设计高水位图8 不规则波作用下堤后透浪系数随周期的变化(H=2.0 m)Fig.8 Influence of period on the wave transmission of irregular wave

9-a 设计低水位9-b 设计高水位图9 规则波作用下堤后透浪系数随周期的变化(H=2.0 m)Fig.9 Influence of period on the wave transmission of regular wave

2.3 透浪系数随入射周期的变化规律

图8～图9分别给出了不规则波和规则波作用下波高H=2.0 m时，四个测点位置堤后透浪系数随周期的变化。从图中可以看出，随着周期的增大，两种水位情况下，无论规则波还是不规则波作用下透浪系数随着入射波周期的增大而增大，且变化比较明显。从试验结果可以看出无论规则波还是不规则波，长波均较短波更易传播至堤后，长波对港内泊稳影响更大，这与相对波长对透射系数的影响规律一致。

2.4 透浪系数随入射波高的变化规律

图10～图11分别给出了不规则波和规则波作用下有效周期13.83 s时，四个测点位置堤后透浪系数随波高的变化。从图中可以看出，随着波高的增大，在两种水位情况下，无论是规则波还是不规则波作用下透浪系数随波高的增大而减小，但总体变化幅度不大。因此在不越浪情况下波高对透浪系数的影响较小。

10-a 设计低水位10-b 设计高水位图10 不规则波作用下堤后透浪系数随波高的变化(T=13.83 s)Fig.10 Influence of wave height on the wave transmission of irregular wave

11-a 设计低水位11-b 设计高水位图11 规则波作用下堤后透浪系数随波高的变化(T=13.83 s)Fig.11 Influence of wave height on the wave transmission of regular wave

2.5 规则波与不规则波作用下透浪系数比较

图12和图13分别给出了波高2.0 m，周期8 s和13.83 s时两种水位下规则波与不规则波作用下透浪系数的变化，从图中可以看出，在相同的试验条件下，规则波透浪系数值比不规则波的透浪系数要小，结果表明在相同试验条件下，不规则波对堤后泊稳影响更大。

12-a 设计低水位12-b 设计高水位图12 规则波透浪系数与不规则波透浪系数的比较(H=2.0 m,T=8 s)Fig.12 Comparison of regular and irregular wave permeability coefficient (H=2.0 m,T=8 s)

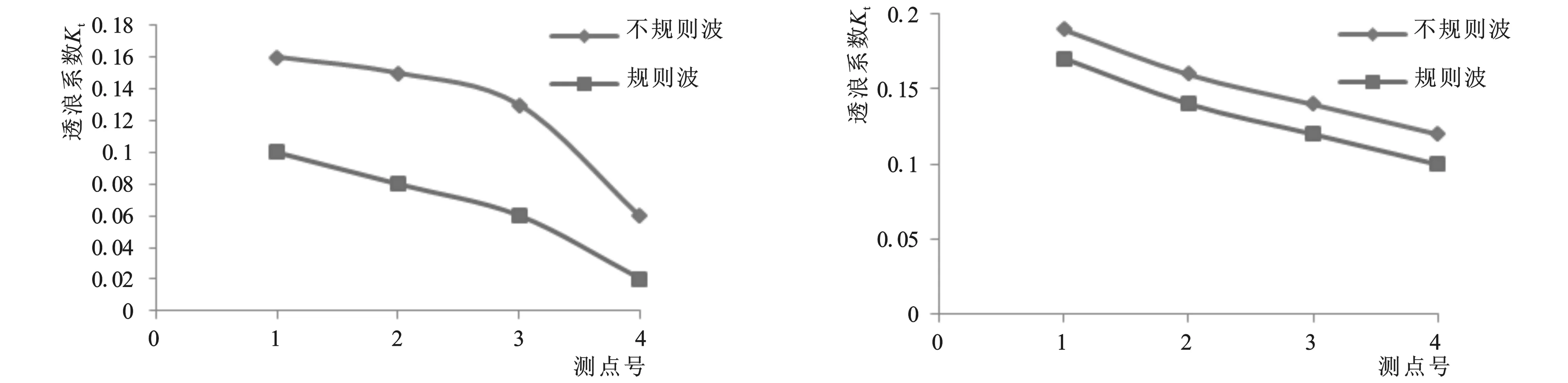
13-a 设计低水位13-b 设计高水位图13 规则波透浪系数与不规则波透浪系数的比较(H=2.0 m,T=13.83 s)Fig.13 Comparison of regular and irregular wave permeability coefficient(H=2.0 m,T=13.83 s)

2.6 透浪系数公式拟合

根据以上影响因素分析可知，透浪系数受入射波周期、入射波高和相对宽度影响较大，基于王登婷[8]、冯卫兵[1]等的研究成果，可得在一定的堤心石级配情况下即本试验中D为常量条件下，拟合得到斜坡堤透浪系数与入射深水波陡H/(gT2)，堤心石相对宽度B/D和堤前相对波高水深比H/d等影响因素相关的计算公式，规则波及不规则波堤后透浪系数经验计算公式分别为(公式中取1#测点处数据作为堤后波高值)

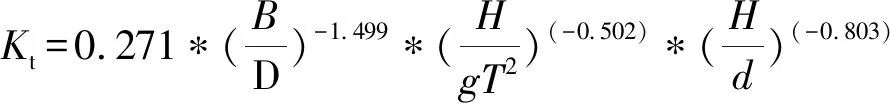
(3)

(4)

式中：B为静水面处堤身宽度，m；D为粒径曲线上小于该粒径块石重量占总重量10%的粒径值，本文中取D值为0.42 m；d为堤前水深值，m；H为入射波高值，规则波公式中为平均波高值，不规则波公式中为有效波高值，m；T为周期，规则波公式中为平均周期，不规则波公式中为有效周期，s。

透浪系数经验公式计算与物理模型试验结果对比见图14所示，规则波情况下计算值与试验值最大相对误差为22.2%，最小相对误差为0.8%，不规则情况下计算值与试验值最大相对误差为11.37%，最小相对误差为1.42%，表明在一定堤心石级配情况下规则波和不规则波透浪系数计算公式拟合效果良好。

14-a 规则波14-b 不规则波图14 透浪系数Kt计算值与试验值对比Fig.14 Comparison of the calculated and test value of the wave coefficient Kt

3 结论

(1)规则波和不规则波情况下，透浪系数均随着相对宽度的增大而减小，在相同的波浪条件下，规则波时相对宽度的影响比不规则波时影响更明显。

(2)规则波和不规则波情况下，相同入射波条件下，透浪系数均随着相对波长的增大而减小，相对波长对堤后透射系数的影响较为敏感。

(3)在相同的入射波高条件下，无论规则波还是不规则波作用下透浪系数均随着入射波周期的增大而增大，且变化比较明显。从试验结果可以看出无论规则波还是不规则波，长波均较短波更易传播至堤后，长波对港内泊稳影响更大。

(4)在波周期不变情况下，透浪系数随着波高的增大而减小，但在不越浪情况下波高对透浪系数的影响较小。

(5)在相同的试验条件下，规则波透浪系数值比不规则波的透浪系数要小，结果表明在相同试验条件下，不规则波对堤后泊稳影响更大。

(6)在一定的堤心石级配情况下，通过对入射波高和入射周期无量纲化分别拟合出在不考虑越浪前提下规则波和不规则波斜坡式防波堤透浪系数公式，通过拟合公式反应出在相同的堤心石级配情况下，堤后透浪系数正比与波浪周期，反比与波高和相对宽度，即与入射深水波陡H/(gT2)和参数B/D、H/d等影响因素相关。通过与试验值对比拟合公式效果良好。