岸礁地形上波浪增水和传递波的数值模拟研究
诸裕良,虞 琦,赵红军,宗刘俊
(河海大学 港口海岸与近海工程学院,南京 210098)
珊瑚礁是在热带和亚热带浅海、由造礁珊瑚骨架和生物碎屑组成的具有抗浪性能的海底隆起[1],在中国台湾岛、海南岛和南海诸岛[2]也分布广泛。根据礁体与岸线的关系可将其分为岸礁、堡礁和环礁[1],其中岸礁沿岸生长并向海延伸。从地形上看,珊瑚礁海岸与常见的淤泥质和沙质海岸存在明显的区别:淤泥质和沙质海岸的底坡一般较为平缓,波浪先在平缓的底坡上发生浅水变形,而后因水深的限制在浅水域破碎,破碎波在岸线附近形成冲泄区;而珊瑚礁由礁前带、礁核带和礁后带组成[1],礁前斜坡通常较陡,礁坪相对平坦,波浪在水深急剧变浅的礁前陡坡上发生浅水变形,随后在礁缘附近破碎,破碎波在坦浅的礁坪上继续传播一段距离后生成新的行进波向礁后传播。
国内外学者对波浪在珊瑚礁地形上的传播变形开展了大量的数值模拟研究,因良好的非线性性能Boussinesq方程数值模型在此方面得到了广泛应用。Skotner和Apelt[3]利用扩展型Boussinesq方程[4],研究了规则波在潜礁上传播过程中时均水位的变化,指出Boussinesq方程可较准确地模拟波浪破碎引起的增减水,仅在强非线性情况下计算的增水值偏小。Nwogu和Demirbilek[5]采用任意水深层Boussinesq方程[6]模拟了岸礁地形上不规则波的传播变形,研究了波高和时均水位的沿程变化、以及由于非线性波波相互作用和波浪破碎等引起的波谱变化。Yao等[7]基于完全非线性Boussinesq方程数值模型[8],模拟了不同岸礁地形上的波浪传播变形,讨论了礁前的坡度和剖面形状对时均水位和波高的影响。Roeber和Cheung[9]采用有限体积法,建立了扩展型Boussinesq方程和浅水方程联合计算模型,模拟了孤立波在岸礁上的传播变形过程,利用试验和观测数据证实了模型能够再现岸礁地形上波浪破碎前后的波面时间过程和谱形变化情况。房克照等[10]建立了高阶Boussinesq 方程和浅水方程联合计算模型,模拟了孤立波在潜礁上的传播和破碎过程。
以往的研究多关注入射波浪条件[11,13]、礁坪水深[12-13]、礁前斜坡[7,12]、礁冠[13]等因素对珊瑚礁上波浪传播变形的影响。但随着珊瑚礁海岸的开发,礁顶工程建设日益增多,这改变了礁坪的长度和礁后岸坡的坡度,诸如此的地形变化对波浪增水和传递波的影响尚鲜有报道。为此,本文采用完全非线性Boussinesq数值模型FUNWAVE-TVD[14],对岸礁地形上波浪的传播变形进行研究,重点在于测试FUNWAVE-TVD对岸礁地形上波浪传播变形的计算性能,研究礁坪长度和礁后岸坡坡度对波浪增水和传递波的影响。
1 FUNWAVE-TVD数值模型简介
Kirby等[15]采用有限差分法建立了完全非线性Boussinesq方程数值模型FUNWAVE。随后Shi和Kirby等[14]在此基础上对控制方程和数值解法等做了若干改进,得到了FUNWAVE-TVD数值模型。
1.1 控制方程与数值解法
FUNWAVE-TVD数值模型的控制方程为
ηt+▽·M=0
(1)
uα,t+(uα·▽)uα+g▽η+V1+V2+V3+R=0
(2)
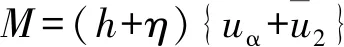
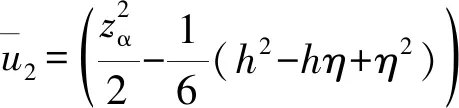
(3)
A=▽·(huα)
(4)
B=▽·uα
(5)
式中:V1、V2、V3是Boussinesq方程的色散项,R是扩散项和耗散项,包括底摩阻项Rf和子网紊动混合项Rs。
FUNWAVE-TVD数值模型采用有限体积和有限差分相结合的空间离散方法,其中,色散项使用常规的有限差分法处理,其他项使用有限体积法求解。模型采用高阶MUSCL-TVD格式处理通量项和一阶导数项,结合HLL近似黎曼求解器计算数值通量,从而使模型具备激波捕捉功能;采用具有强稳定性的、步长三阶Runge-Kutta法进行时间积分,使用CFL准则限制时间网格步长以保证计算收敛。
1.2 边界条件与造波
FUNWAVE-TVD可以模拟固壁边界、吸收边界和动边界。其中,固壁边界采用比较常用的处理方法:令固壁处的法向速度、波面的法向梯度和切向速度的法向梯度都为零,即v=0,ηy=0,uy=0。
吸收边界通过设置海绵层来实现,数值处理方法为在x、y方向的动量方程中分别加入人工阻尼项
(6)
(7)
式中:w1、w2、w3分别对应牛顿冷却项、粘性阻尼项和海绵层过滤项。海绵层宽度通常取2~3个波长。
动边界采用干湿网格法处理,令干网格边界面上的法向通量为零,同时将镜面边界条件运用于四阶MUSCL-TVD格式和干网格色散项的离散,并对干网格处的波速进行修正
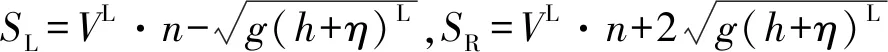
(8)

(9)
模型入射波边界使用Wei等[16]提出的源函数造波法,在广义形式的线性化Boussinesq方程和浅水方程中加入造波源函数项f(x,y,t)后,连续方程和动量方程可分别表达为
ηt+h▽u+α1h3▽2(▽u)=f(x,y,t)
(10)
ut+g▽η+αh2▽2ut=-g▽P
(11)
式中:α1和α为方程参数,取不同的值可得到不同形式的Boussinesq方程;P为压力分布。
1.3 波浪破碎与底摩阻的处理
FUNWAVE-TVD通过关闭Boussinesq方程中的非线性项和色散项,将Boussinesq方程退化为非线性浅水方程来模拟波浪破碎。模型选择波高水深比H/d作为方程的切换变量,对于任一网格单元,当H/d≥0.8[17]时,则认为波浪发生破碎,此时非线性项和色散项不参与计算。
模型考虑底摩阻的方法是在动量方程中加入底摩阻衰减项
Rf=-Cd×uα|uα|
(12)
式中:Cd为底摩阻系数,Shi等[14]认为该参数在实验室地形下不敏感,可取为0或者0.001。
2 岸礁地形上波浪传播变形的数值模拟
2.1 物理试验简介及数值模型设置
为研究风浪对礁坪波浪增水和岸坡波浪爬高的影响,Demirbilek等[18]在密歇根大学的风浪水槽中开展了80多组次的波浪水槽模型试验,包括波浪试验、风试验和风浪试验。本文将利用其中的部分试验,对FUNWAVE-TVD关于岸礁地形上波浪传播变形的计算效果进行检验。
Demirbilek等[18]的试验设置如图1:试验断面的礁前斜坡为三段式复合斜坡,礁坪长4.8 m,高0.5 m,礁后岸坡坡度为1:12。沿程布置了九根电容式波高仪(G1~G9),其中G1~G3位于坡脚前,用以分离入反射波,G4~G6、G7~G9分别位于礁前斜坡和礁坪,用以记录沿礁波面时程的变化,礁后岸坡上布置了一根1 m长的电容式爬高仪测量波浪爬高。试验采用不规则入射波,入射波谱型为JONSWAP谱,谱峰升高因子γ=3.3。波高仪和爬高仪的采样频率fs均为20 Hz,造波开始后立即采样,采样时间为15 min。
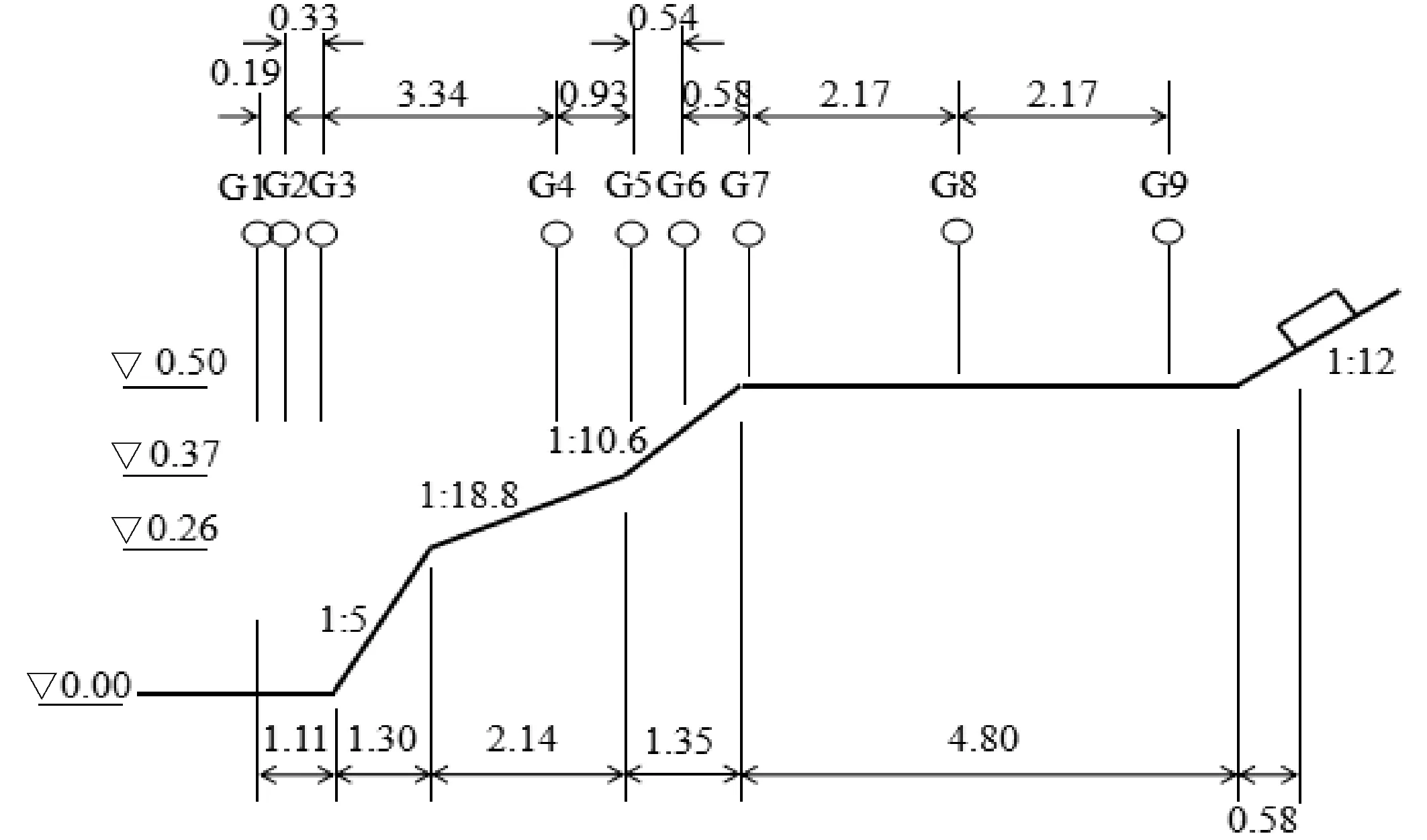
图1 试验设置图(m)Fig.1 Experimental setup(m)
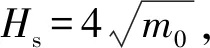

表1 入射波浪条件表Tab.1 Incident wave conditions
2.2 模型检验与参数敏感性分析
2.2.1 模拟结果对空间网格步长Δx的敏感性分析
空间网格步长Δx会影响模型的数值耗散和计算效率。为了测试模型计算结果对Δx的敏感性,针对Test33(礁坪无水)和Test45(礁坪淹没)两组试验,分别以Δx为1/16Lp、1/32Lp和1/64Lp进行了计算,图2给出了不同Δx时有效波高和时均水位的沿程变化,为方便比较,试验值也绘于图中。结果显示:数值结果对Δx比较敏感,Δx较大时沿程波高计算值较试验值明显偏小,这是模型数值耗散过大所致,特别是在礁前斜坡段,波高迅速减小,数值耗散导致的波高衰减显著强于浅水变形引起的波高增大,此时模型无法合理描述浅水变形和波浪破碎引起的波高变化。从时均水位看,Δx较大时减水现象不明显且礁坪增水幅度明显偏小,根据Tait[19]的研究,波浪的增减水与破碎波高成正相关,因为Δx较大时的数值耗散使破碎波高的计算值偏小,所以减水值与增水值亦偏小。


2-a1 Test33模拟与试验有效波高沿程变化图2-a2 Test45模拟与试验有效波高沿程变化图


2-b1 Test33模拟与试验时均水位沿程变化图2-b2 Test45模拟与试验时均水位沿程变化图


2-c1 Test33地形、水位示意图2-c2 Test45地形、水位示意图图2 Test33和Test45模拟与试验有效波高、时均水位沿程变化图Fig.2 Predicted and measured significant wave height and mean water level variation for Test33 and Test45
为进一步探究Δx对波浪破碎模拟效果的影响,统计了不同Δx时的波浪破碎位置,并用相应灰色竖线标记在图2-a中。据此可知,在Δx较大时,模型预测的破碎位置后移且破碎范围缩窄,这是因为模型以波高水深比作为破碎阈值,过大的数值耗散使波高计算值偏小,所以波浪在水深更浅时才发生破碎,从而造成破碎位置后移。图3和图4分别给出了波浪破碎前四根波高仪处模拟波谱与试验波谱的比较,再次证明Δx过大带来的数值耗散会使波能偏小,同时从图中可以进一步看出数值耗散主要发生在不规则波中频率大于谱峰频率的高频段。

图3 Test33模拟与试验波谱图Fig.3 Predicted and measured wave spectra at selected gauges for Test33
比较图2中有效波高和时均水位的计算结果和试验值可知,在Δx取1/64Lp时,二者吻合良好,数值结果能较好地反映波浪在岸礁上传播过程中波高和时均水位的变化。并且从图3~图4中也可以看出,在Δx取1/64Lp时,模型能较好地描述不规则波中各频率的波能分布,在二倍频(两倍的入射波谱峰频率)处模拟值与试验值也基本吻合,说明模型具有较高的计算精度。

图4 Test45模拟与试验波谱图Fig.4 Predicted and measured wave spectra at selected gauges for Test45
2.2.2 模拟结果对底摩阻系数Cd的敏感性分析
底摩阻系数Cd的取值影响数值计算中的底摩阻耗散量,Shi等[14]认为在实验室条件下,模型对Cd不敏感,建议取0或0.001。但Nwogu和Demirbilek[5]在运用物理试验对Boussinesq模型进行检验时发现:Cd的取值会影响礁坪段波浪模拟的精度。为确定适合本次试验计算的Cd值并测试模拟结果对Cd的敏感性,对Test33和Test45两组试验再次进行计算。Demirbilek试验为了减小摩阻对试验结果的影响,使用了相对光滑的聚氯乙烯板制作地形,但实际操作时水槽内无法做到绝对光滑,因此本文模型计算测试了Cd为0.001和0.006两种情况。图5对有效波高和时均水位的计算值与试验值进行了比较。从图中可以看出,模拟结果对Cd很不敏感,Cd取0.001和0.006对礁前斜坡上的波高和沿程时均水位几乎没有影响,仅小幅度地影响了礁坪上的传递波高,且Cd越大,传递波高越小。对比计算值与试验值可知,Cd取0.001时,数值结果与试验数据吻合良好,模型能更好地模拟岸礁地形上波高和时均水位的沿程变化。


5-a1 Test33模拟与试验有效波高沿程变化图5-a2 Test45模拟与试验有效波高沿程变化图


5-b1 Test33模拟与试验时均水位沿程变化图5-b2 Test45模拟与试验时均水位沿程变化图


5-c1 Test33地形、水位示意图5-c2 Test45地形、水位示意图图5 Test33和Test45模拟与试验有效波高、时均水位沿程变化图Fig.5 Predicted and measured significant wave height and mean water level variation for Test33 and Test45
2.2.3 模拟结果对破碎阈值H/d的敏感性分析
FUNWAVE-TVD以波高水深比H/d作为破碎模型启停的判据变量,Tonelli和Petti[17]建议将H/d的阀值取为0.8。为验证该值在岸礁地形上的适用性以及测试模拟结果对H/d阀值的敏感性,对表1中的八组试验进行了模拟。诸裕良等[20]通过波浪水槽试验分析得出:珊瑚礁地形上波浪破碎时H/d大致分布在0.7~1.1之间,故计算中H/d的阀值分别设为0.6、0.8、1.0和1.2。因为波浪破碎后会在礁坪产生增水,破碎波在礁坪上传播一段距离后生成新的行进波,随后行进波在礁后岸坡上爬落,所以H/d的取值对波浪破碎以及破碎后的一系列水动力过程都会产生影响,因此以礁坪上的传递波高、增水和礁后岸坡上波浪爬高的相对误差作为H/d阀值的评价标准。具体统计方法为:计算各组次下波高仪G8和G9处(G8和G9位于礁坪中后段,此时波浪已基本完成破碎,传递波高和增水都达到了相对稳定的状态)的有效波高和增水,算出模拟值与试验值的相对误差,将波高和增水在两个波高仪处的相对误差分别平均,得到各组次的传递波高相对误差和增水相对误差。同时统计各组次下礁后岸坡上波浪爬高R2%的相对误差。图6以破波相似参数ξ0(ξ0=tanα/(H0/Lp0)0.5),深水波高H0和深水谱峰波长Lp0均基于微幅波理论求得,H0=Hs/ks,ks为浅水变形系数,Lp0=gTp2/2π,tanα取礁前斜坡的平均坡度)为横坐标,给出了H/d各阈值下传递波高、增水和爬高的相对误差以及三者整体的相对误差图。从图6-a~6-c可以看出,传递波高和增水的相对误差都在40%以内,爬高误差稍大,但除了一组误差较大外,其余各组也都在65%以内。从图6-d中可以看出模拟结果对H/d较为敏感,H/d为0.8时,数值计算结果与试验值的整体误差最小,所以模拟岸礁波浪传播变形时H/d取0.8数值计算结果更准确。


6-a 传递波高相对误差统计图6-b 增水相对误差统计图6-c 爬高相对误差统计图6-d传递波高、增水和爬高的总相对误差统计图图6 传递波高、增水、爬高以及整体相对误差统计图Fig.6 The statistics of the relative error of transmitted wave height, wave setup, wave runup and overall
通过以上的岸礁波浪试验模拟可以发现:FUNWAVE-TVD适用于岸礁地形上波浪传播变形的数值模拟,能够较合理地预测岸礁地形上波浪的时均水位变化、波高变化、礁后岸坡上波浪爬高等水动力过程。
3 礁坪长度和礁后岸坡坡度对波浪增水和传递波的影响研究
随着珊瑚礁海岸的开发和资源利用,礁顶工程建设日益增多,这改变了礁坪的长度和礁后岸坡的坡度,为掌握此类变化对礁坪增水和传递波的影响,利用FUNWAVE-TVD模型开展数值模拟研究。以图1的岸礁地形为原型,每次模拟仅改变礁坪长度B或礁后岸坡坡度m。为考虑极端情况,选取Demirbilek等[18]的岸礁波浪试验中入射波高较大的组次Test31(有效波高Hs=9.2 cm,Tp=2 s,hr=1.6 cm)作为入射波浪条件。
3.1 礁坪长度B对波浪增水和传递波的影响
为消除水深对模拟结果的影响,基于微幅波理论将谱峰波长换算至深水,设置礁坪长度B分别为Lp0、2.5Lp0、5Lp0、7.5Lp0和10Lp0。不同礁坪长度时的有效波高和时均水位的沿程变化如图7所示,可见:随着礁坪长度减小,礁坪增水变化很小,但传递波高会逐渐增大。为更为直观地考察增水和传递波与礁坪长度的关系,图8给出了波浪增水、传递波高和爬高随B的变化图。为减少礁后岸坡上波浪浅水变形及破碎对传递波和礁坪增水的影响,以礁后岸坡坡脚前1 m处的有效波高和时均水位作为传递波高值和礁坪增水值,以礁后岸坡上累计频率为2%的爬高R2%作为岸坡爬高值,由图8可知:当B从10Lp0减小到5Lp0,爬高几乎不变,传递波高和增水会略有波动,但整体变化较小,其中波高增大了10%左右,增水减小了2%左右;当B继续减小时,传递波高和爬高不断增大且增大速度越来越快,增水略有减小,B从5Lp0减小到Lp0过程中传递波高增大了20%,爬高增大超过70%,增水仅减小了6%。总的来看,礁坪长度缩短对增水几乎没有影响,但会使传递波高和爬高增大。


7-a 不同礁坪长度下有效波高沿程变化图7-b 不同礁坪长度下时均水位沿程变化图7-c 不同礁坪长度下地形、水位示意图图7 不同礁坪长度下有效波高、时均水位沿程变化图Fig.7 Variations of significant wave height and mean water level over reef profile with different reef flat lengths

8-a 不同礁坪长度下传递波高变化图8-b 不同礁坪长度下增水变化图8-c 不同礁坪长度下爬高变化图图8 不同礁坪长度下传递波高、增水和爬高变化图Fig.8 Variations of transmitted wave height, wave setup and wave runup with different reef flat lengths


9-a 不同礁后岸坡坡度下有效波高沿程变化图9-b 不同礁后岸坡坡度下时均水位沿程变化图9-c 不同礁后岸坡坡度下地形、水位示意图图9 不同礁后岸坡坡度下有效波高、时均水位沿程变化图Fig.9 Variations of significant wave height and mean water level over reef profile with different beach slopes
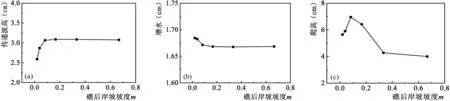

10-a 不同礁后岸坡坡度下传递波高变化图10-b 不同礁后岸坡坡度下增水变化图10-c 不同礁后岸坡坡度下爬高变化图图10 不同礁后岸坡坡度下传递波高、增水和爬高变化图Fig.10 Variations of transmitted wave height, wave setup and wave runup with different reef beach slopes
3.2 礁后岸坡坡度m对波浪增水和传递波的影响
根据人造岸坡和天然岸坡的坡度范围,设置礁后岸坡坡度m分别为1:1.5,1:3,1:6,1:12,1:25,1:50。不同礁坪长度时的有效波高和时均水位沿程变化如图9所示:随着礁后岸坡坡度增大,礁坪增水变化很小,但传递波高会略有增大。图10给出了礁后岸坡坡脚前1 m处的传递波高和增水值随m的变化、以及岸坡上的爬高R2%随m的变化图。据此可知:当m小于1:12时,传递波高和爬高随着m的增大而增大,m从1:50增加到1:12的过程中,传递波高增大了18%,爬高增大了19%,增水增大不到1%;随着m继续增大,传递波高和增水都趋于不变,爬高先急剧减小后下降的速度变小,陈国平等[21]关于不规则波爬高的模型试验研究也得到了这一规律,即爬高随坡度先增大后减小。由此可见,礁后岸坡坡度增大不影响礁坪增水,在坡度较缓的范围内,坡度增大会使传递波高和爬高增大但增大的有限,随着坡度进一步增大,传递波高不再受影响,但爬高会先显著减小后减小的趋势变缓。
4 结论
本文利用完全非线性Boussinesq方程数值模型FUNWAVE-TVD,对珊瑚岸礁地形上的波浪增水和传递波进行了数值模拟研究,得到以下结论:
(1)模拟岸礁波浪试验的数值结果与试验值吻合良好,说明模型可以对波浪在岸礁上的传播变形过程进行有效计算,适用于岸礁地形上波浪传播变形的数值模拟研究。
(2)数值模型的敏感性计算分析显示:在利用该模型模拟岸礁波浪传播变形时,建议空间网格步长取1/64Lp,破碎阈值取0.8,实验室条件下的底摩阻系数取0.001。
(3)岸礁礁坪长度和礁后岸坡坡度改变基本不影响礁坪增水;当礁坪长度小于5Lp0后,继续减小礁坪长度会使传递波高和爬高增大且增大速度不断加快;礁后岸坡坡度在坡度较缓的范围内增大时,传递波高和爬高随之增大,随着坡度进一步增大,传递波高不再受影响,但爬高会先急剧减小后减小速度变缓。

