舰炮摆弹运动弹药振动的影响因素分析

叶 辛，孙世岩，谭 波

(海军工程大学, 武汉 430000)

大口径舰炮通过后坐时弹簧释放储存的能量完成规定的摆弹动作，是一个时间短、速度快的高动态过程。在摆弹机构的高频重复过程中，弹药与抱爪发生碰撞，对弹药的振动产生影响。弹药径向相对薄弱，不断的冲击振动使其存在安全隐患。司志桧[1]考虑发射过程中弹丸前定心部与膛壁的摩擦，对弹丸膛内运动进行仿真计算，研究了弹丸与身管配合间隙对弹丸起始扰动的影响。刘成柱[2]考虑了弹带膛线与弹丸的接触碰撞，研究了车载炮上架对弹丸起始扰动的影响。刘宁[3]考虑火炮射击过程中弹丸与身管的接触碰撞，建立身管振动方程，研究了弹管间隙对身管振动的影响。於崇铭[4]考虑弹药运输过程中的持续振动，通过实测加速度信号与施加白噪声激励信号，分析了弹药包装对振动的影响。于会杰[5]考虑弹丸运动冲击下身管振动规律，研究了弹丸激励下身管的振动响应。

以往对摆弹过程的研究一般较少考虑弹药振动的情况，多以摆弹机构为对象建立刚-柔耦合动力学模型，重点考虑材料弹性属性引起的柔性变形[6-9]，本文对弹药建立动力学模型，考虑抱弹爪与弹药的包合程度，基于牛顿定律以及刚体动力学理论，运用Matlab软件进行模拟仿真，并通过简化抱弹器模型，将数值运算结果与简化模型输入ADAMS虚拟样机中，分析改变参数对弹药振动引起的弹药状态变化。

1 弹药摆弹运动工作原理

在某中大口径舰炮供弹运动过程中，弹药从回转部分供弹系统的扬弹机提升到摆弹机，再由摆弹机摆臂向发射系统任一射角上的转弹机传递炮弹。摆弹动作通过摆弹机完成，它主要由弹簧、齿条、齿轮、摆臂以及抱弹装置组成。弹药被发射出去后，炮管后坐压缩弹簧储存能量，当炮管复进时，弹簧释放能量。弹簧与齿条连接，在弹簧弹力作用下齿条沿着导轨运动，齿条和齿轮啮合使齿轮转动，摆臂与齿轮固连，随着齿轮一起转动，抱弹装置抱紧弹药并准确定位完成摆弹。摆弹机构结构简图如图1。

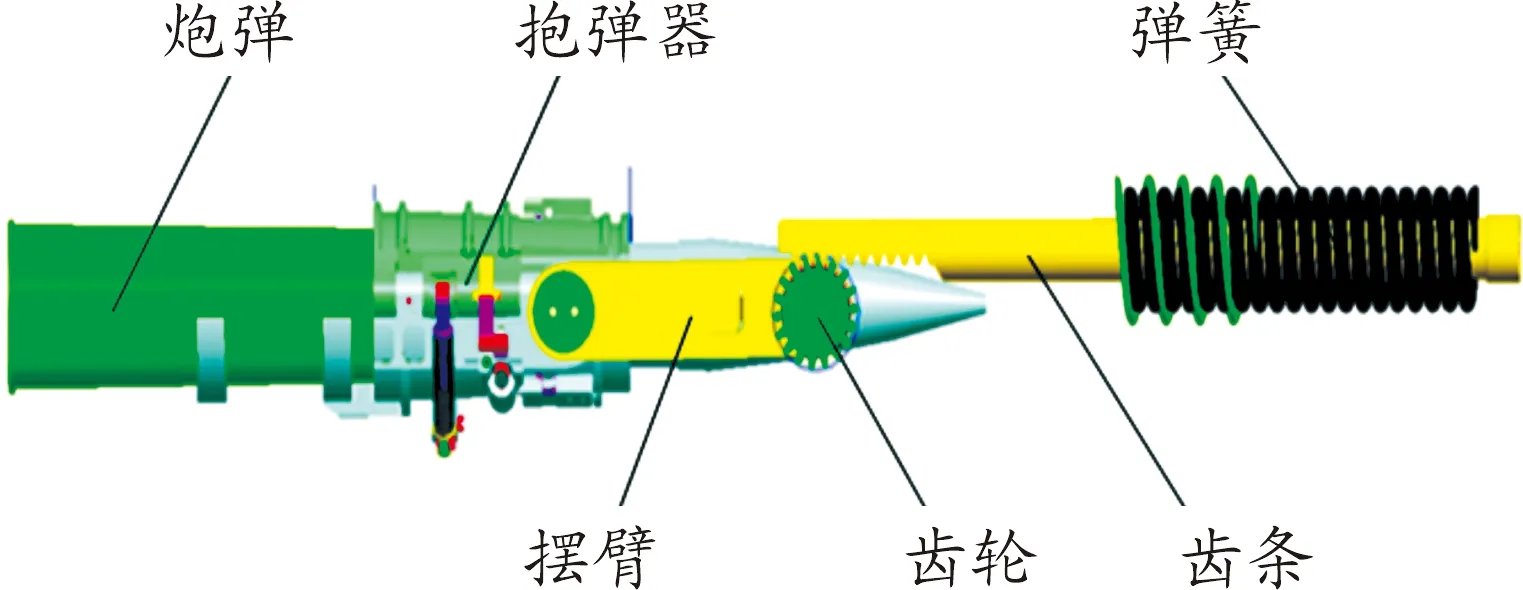
图1 摆弹机构结构简图

摆弹是一个先加速后减速的过程，在这个过程中弹药与抱爪紧密接触。由于设计上的误差，弹药与抱爪之间存在一定的间隙，从而使弹药与抱爪发生碰撞，若将抱弹器视为相对静止状态，则弹药在进行摆弹运动的同时在不断振动。

2 运动模型建立

以某中大口径舰炮弹药为研究对象，建立弹药摆弹过程的动力学模型，应用多刚体动力学理论对弹药进行计算和仿真[10]。g为重力加速度，规定作用力以右为正，转矩以顺时针方向为正。

齿条受力分析如图2所示。

Fc为齿条对齿轮的作用力，Fc′为齿轮对齿条的反作用力，两力大小相等，即：

Fc=Fc′

(1)

图2 齿条受力分析

根据胡克定律弹簧驱动力Ft满足：

Ft=F0+K·ΔL-K·x

(2)

x=θ·Rc

(3)

式中：F0为安装时弹簧预压力；ΔL为后坐储能时弹簧压缩的长度；x齿条最大位移；Rc为齿轮分度圆半径。

根据牛顿第二定律，齿条运动满足：

(4)

图3为摆臂构件受力分析图。以弹药为研究对象，并将弹药视为刚体，根据刚体转动惯量定义，整个摆弹装置和弹药的转动惯量J为：

(5)

弹药质心对齿轮轴心产生的重力矩为：

TD=GDLsinθ

(6)

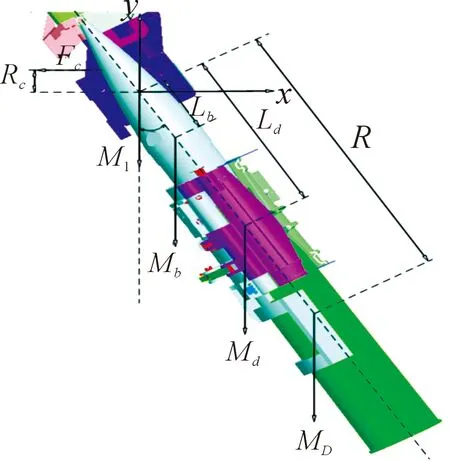
Mb为摆臂质量；MD为弹药质量；Md为抱弹器质量；Ml为齿轮质量；R为弹药重心距离齿轮轴心距离；Ld为抱弹器重心距离齿轮中心距离；Lb为摆臂重心距离齿轮轴心距离

图3 摆臂构件受力分析

根据刚体动量矩定理，联立式(1)、式(2)、式(5)、式(6)，整理得弹药绕齿轮轴心转角运动方程[11]为：

(7)

在舰炮所有射角中，0°射角时弹药摆角几乎最大，因此耗时最长，摆臂停止时的角速度最大，产生冲击较大，振动衰减时间较长。故考虑在最恶劣条件0°射角情况下，即摆臂最大摆角θ为90°时进行摆弹动作，要求弹药摆弹一次在0.7 s[3]内完成。选取弹簧刚度K=79.6 N/mm，弹簧预压力F0=12.3 kN，弹药质量MD=54 kg，弹药质心距齿轮轴心距离L=900 mm，摆弹一次经历时间t=0.7 s[8]。通过软件Matlab采用四阶Runge-Kutta法编程，得到摆角随时间的变化曲线如图4所示。

如图4、图5所示，随着时间不断变化，摆弹角速度先增大后减小。摆到0.43 s时，角速度达到最大值3.017 rad/s；由于惯性力及抱弹器作用，弹药继续摆弹运动，同时弹药开始作减速运动，角速度减小，到0.7 s，摆弹到90°，此时角速度为2.24 rad/s。

图4 摆角θ随时间t的变化曲线

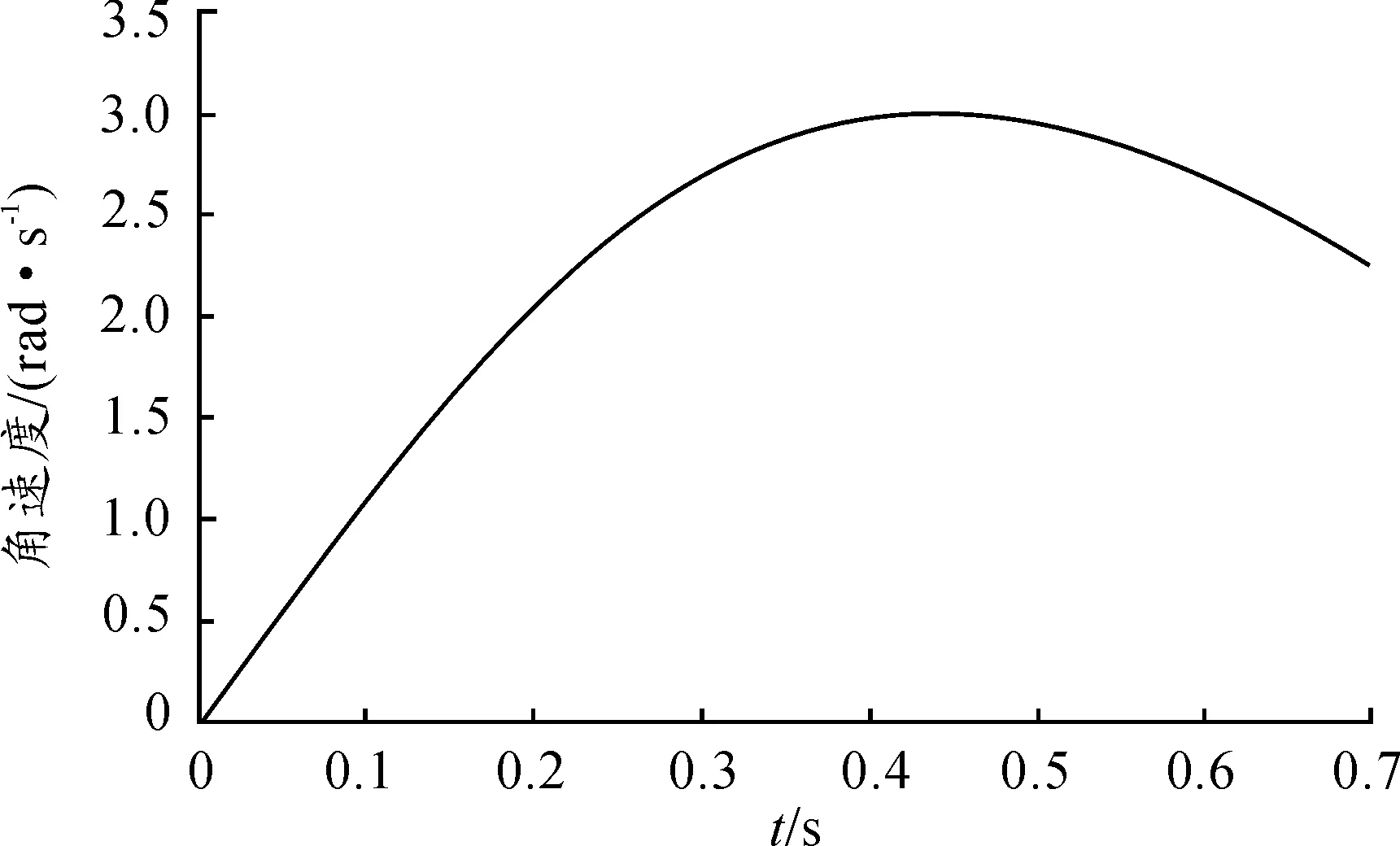
图5 摆弹角速度随时间t的变化曲线

3 摆弹运动安全性分析

摆弹过程中弹药受到抱弹爪施加的径向作用力，由相对静止状态突然转变为运动状态，从而使弹药与抱弹爪发生碰撞。摆弹是一个持续的变速过程，因此弹药与抱弹爪不断碰撞，使弹药在径向方向处于相对振动状态，导致弹药的安全性降低。

3.1 运动模型简化与仿真

由于抱弹器结构复杂，各部分小零件在实际机械运动时才能实现其功能，因此将相关结构进行简化，抱弹器简化模型如图6所示。

图6 抱弹器简化模型

抱弹器托体部分与弹药接触面积较大，通过改变抱弹器托体内表面直径的大小，从而控制抱弹器与弹药的包合程度。抱弹器托体内表面直径与弹药药筒直径越接近，包合程度越好，反之，弹药与抱弹器之间间隙越大。

在ADAMS中打开摆弹模型，设置抱弹器与弹药外壳材料属性为结构钢，药筒内装药进行配重设置，其他参数选择默认数值。添加旋转副，使抱弹器绕轴运动。并在抱弹器与弹药之间，以及抱弹卡锁与弹药之间设置接触约束，运动仿真如图7所示。

图7 摆弹运动仿真

3.2 模拟仿真试验计算

根据该型舰炮弹药药筒直径实际测量尺寸为160.75 mm，且抱弹器托体部分内表面直径与弹药药筒之间存在一定间隙，故设置抱弹器托体部分内表面直径为较大值170 mm进行仿真。将Matlab计算数据存为.txt格式，并导入ADAMS中，在ADAMS中Independent Column Index状态栏里输入1，表示.txt中的第一列为变量。设置模拟仿真时间为0.7 s，仿真步数为150步，仿真结果如图8所示。

图8 ADAMS运动仿真结果

图8中曲线反映了弹药内坐标为(100.0，0.0，-100.0)的标记点在x轴、y轴、z轴上相对于转轴转动的角速度。在x轴、y轴正负方向上角速度分别出现三次峰值，其中在x轴上第一次峰值较小，第三次峰值较大，相反，在y轴上第一次峰值较大，第三次峰值较小，在两轴上第二次峰值差别较小。且在x轴和y轴上，分别在同时刻角速度为0 rad/s。由于标记点z轴垂直于抱弹器摆动平面，故标记点在z轴角速度变化最接近输入驱动曲线图5，由于弹药在上摆过程中不断与抱弹器碰撞，标记点在z轴角速度不断发生振动。

标记点在x轴与y轴上的角速度相互垂直，根据矢量定理可将两个方向振动合为一个总振动，角速度总振动曲线如图9。

图9 角速度总振动曲线

4 弹药摆弹振动影响因素分析

摆弹过程中，弹药与抱弹器紧密接触，两者的接触对弹药在抱弹器中的振动产生直接影响。由于制造工艺的误差以及训练使用的磨损，弹药与抱弹器接触面积在一定范围内不断波动。通过调整抱弹器托弹部分内表面直径，可以改变抱弹器与弹药接触面积。因此以抱弹器托弹部分内表面直径为变量，通过改变直径的大小，研究弹药在抱弹器中振动情况。分别取抱弹器托弹部分内表面直径为160 mm、162 mm、165 mm、168 mm、170 mm进行模拟仿真，得到角速度总振动曲线如图10。

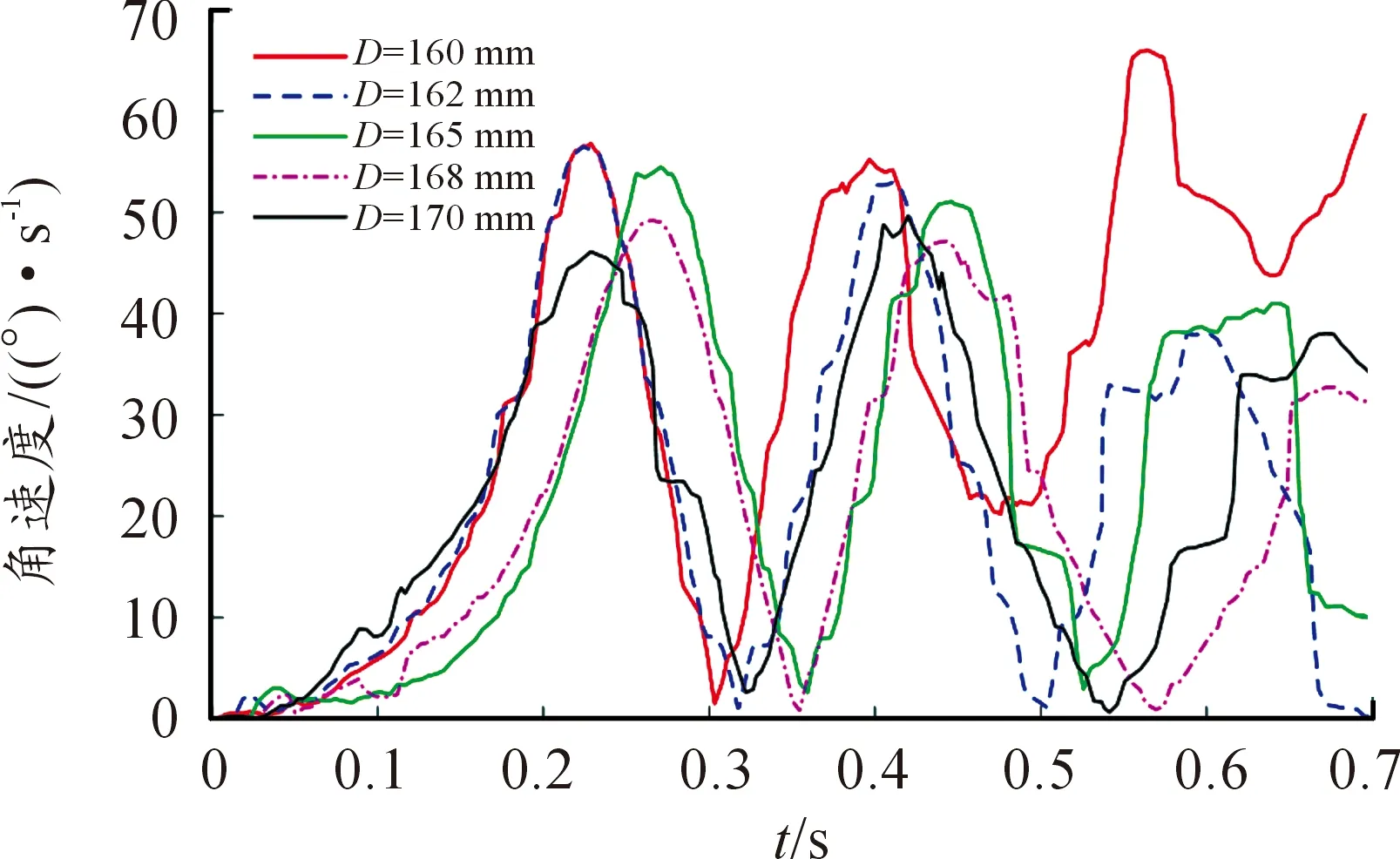
图10 不同直径时的角速度总振动曲线

从图中可以看出，弹药主要出现了3次较大的波峰，出现波峰的时间也较为集中。且第一、第二个波峰峰形规则，第三个波峰峰形不规则。这说明弹药前两次振动为规律性振动，可以反映弹药摆弹过程中的振动状态。

随着弹药直径D的增大，不同曲线峰值先向右移，而后再向左移，这说明出现波峰的时间先变长再缩短，则在取不同直径D时，会有一个波峰出现时的时间最长；且当直径D为168 mm时，其第一个波峰与最小波峰峰值相差无几，而第二、第三个波峰峰值都是最小，则D为168 mm时弹药振动情况相对其他情况较为缓和。综上所述，直径D在160～170 mm间取值时，存在一个数值使弹药振动幅度最小。因此适当选取抱弹器托弹部分内表面直径大小，能够减小弹药在抱弹器中的振动幅度，有助于提高弹药径向方向安全性。

5 结论

1) 弹药与抱弹器的间隙是影响弹药安全性的重要影响因素，通过分析，有助于更好的掌握弹药安全性能。

2) 合理确定抱弹器托弹部分内表面直径大小，能够减小弹药在抱弹器中的振动幅度，提高弹药的安全性。