基于威力场的导弹队形选择方法

杨秀霞，罗 超，张 毅

(海军航空大学， 山东 烟台 264001)

随着信息技术的发展，现代战争已演变为体系与体系间的对抗[1]。以导弹编队为例，现代空战作战样式已经演变为：先以大规模编队飞行，在接近目标时将大规模编队转换为小规模编队作战，然后在小规模编队内依据协同优先权进行目标分配[2]。作为战术层面的重要一环，合适的编队队形可以在一定程度上弥补敌我双方在装备上的性能差异或更好发挥体系作战的优势[3]。因此在不确定信息下如何选择最佳的编队队形非常值得研究。

目前，针对导弹编队队形选择和优化的研究还比较少。其中文献[2-3]以敌我损失比作为目标函数，采用遗传算法对编队队形进行优化。文献[4]在利用市场机制完成目标分配的基础上，构造适应度函数作为优化评估标准，最后利用自适应遗传算法完成大规模编队。为了定量分析编队队形参数对导弹编队作战的影响，文献[5]建立了编队作战效能指标体系，并利用演化算法对编队队形进行优化设计。以上方法存在所提的模型简单、将态势信息与武器装备孤立的特点，采用的智能算法复杂程度高、实时性较差，不适用于实战环境下队形选择。本文提出了一种基于威力势的导弹攻击队形选择方法，该方法能够根据实际战场环境，通过战场指挥人员的主观认知，选择出合适的编队队形，克服战场环境的不确定性，具有一定的应用价值。

1 导弹威力场模型

1.1 导弹威力场模型的构建

导弹威力场模型主要考虑导弹探测能力、生存能力、通信能力、攻击能力等4个方面因素，其模型为[6-7]：

e=e(x,y,z,xT,yT,zT)=ed(ω1ew+ω2es+ω3ec)

(1)

式(1)中，(x,y,z)表示惯性坐标系下导弹的位置坐标；(xT,yT,zT)表示惯性坐标系下目标的位置；ed表示导弹的探测能力；ew表示导弹的攻击能力；es表示导弹的生存能力；ec表示导弹的通信能力；ω1、ω2、ω3分别表示攻击能力、生存能力、通信能力的权重值。

1) 攻击能力

攻击能力模型为[8-9]：

ew=In(1+AM)

(2)

式(2)中，AM表示导弹的攻击能力参数，具体表达式为：

(3)

式(3)中，KD为制导方式修正系数，半主动雷达末制导KD=1，主动雷达末制导KD=1.5；Ph为导弹单发命中概率；φm为导弹攻击范围角；nmax为导弹最大可用过载；ωmax为导弹最大跟踪角速度；r为导弹距计算点的距离；rmax为导弹最大射程；rmin为导弹最小攻击距离。

2) 探测能力

对目标探测设备主要包括雷达和红外搜索跟踪装置，因此目标探测能力参数包括两个部分:雷达探测能力参数ADR和红外探测能力参数ADIR。探测能力模型可表示为：

ed=In(1+ADR+ADIR)

(4)

雷达探测能力参数ADR可表示为：

(5)

式(5)中，RTR表示雷达最大搜索距离；θR为雷达最大搜索方位角；PTR为目标发现概率；m1为雷达能同时跟踪的目标数量；K1为雷达体制衡量系数。

红外探测能力参数ADIR可表示为：

(6)

式(6)与式(5)的参数含义基本相似，其中K2为红外体制衡量系数。

3) 生存能力

导弹生存能力模型建立如下：

es=In(1+As)

(7)

式(7)中，As为生存能力参数，具体表达式为：

(8)

式(8)中，L表示导弹全长；W表示导弹翼展；Rcs表示导弹雷达有效反射面积；Av表示导弹表面积；Ave表示导弹易损性部位面积。

4) 通信能力

强大的数据通信能力可以很大程度上提高导弹编队的作战能力。导弹通信能力模型可表示为:

(9)

式(9)中，Pc表示数据链通信设备的可靠性；dmax表示数据链最大通信距离；ri表示导弹与第i枚导弹成员的距离。

1.2 威力场的叠加

设在整个战场空间中，我方有N枚导弹，则总的正威力场叠加效果为：

e+=e1++e2++…+eN+

(10)

即空间中任一点正威力场的大小等于战场空间内我方所有导弹在该该点产生的威力之和。同理，设敌方有M个作战单元，则总的负威力场的叠加结果为：

e-=e1-+e2-+…+eM-

(11)

在整个战场空间中，正威力场和负威力场同时存在，各自产生的正负势场互不相关。在威力场中，势场相等的点连成的空间曲面称为等势面，在威力场的某一平面内，势相等的线构成的线叫等势线。

2 基于威力场的态势评估方法

设A1={1,2,…,a1}，B={1,2,…,b}。根据1.1节的导弹威力势模型构建导弹的威力矩阵E=[eij]a1×b，其中eij表示第i枚导弹的第j项能力，i∈A1，j∈B。

因实际作战中目标信息存在一定的不确定性，所以对目标威力的评估不能直接采用对我方导弹评估的方法。

设M={1,2,…,m}，N={1,2,…,n}。建立以导弹能力参数为元素的评价指标集合为：

U={u1,u2,…,um}

(12)

式(12)中，ui(i∈M)表示U中第i个能力指标元素。

建立评价等级集

Q={q1,q2,…,qn}

(13)

式(13)中，qj(j∈N)表示第j种评价等级的隶属度，评价等级可以采用清晰数、模糊数和简洁评语等形式来表示[10]。

由于不同导弹性能之间存在差异，这里以我方导弹为标准对各项能力指标进行评估，并依据0.1～0.9标度法给出评估矩阵C：

C=[cij]n×m

(14)

建立模糊关系矩阵Y:

(15)

式(15)中，yij表示U中能力指标元素ui对应于Q中评价等级qj的可能性，由作战指挥人员确定；s为作战指挥人员的数量；φij(i∈M,j∈N)为指标ui被评定为qj的次数。

由式(14)和式(15)可以得到模糊综合评估模型[11]：

T=CYT=[t1,t2,…,tm]

(16)

式(16)中，ti(i∈M)为第i个能力指标参数的评估值。

记A2={1，2，…，a2}，根据式(12)～式(16)可以得到目标各项能力参数的评估值，在按照式(1)～式(9)计算得出第i个目标第j个能力值teij(i∈A2,j∈B)。由此可以构建目标威力评估矩阵TE=[teij]a2×b。

3 仿真分析

设我方共有3枚导弹，编号为1～3，其中2号和3号导弹型号相同。1号导弹和2号导弹能力指标分别见表1和表2。

敌方共有3枚能力不祥的导弹进行拦截，编号分别为4～6。其中4号弹和5号弹型号相同，其位置坐标分别为(150,150,8)、(150,160,8)和(160,150,8)。

首先计算我方导弹威力势，构建威力矩阵。

依据表1和表2中参数，由式(1)～式(9)计算出我方导弹的各项能力并构建威力矩阵为：

对目标威力进行评估，构建目标威力评估矩阵。这里以我方1号导弹的各项能力作为评估标准，以攻击能力为例进行评估。首先根据式(12)建立评价指标集合U：

U={Ph,φm,ωmax,nmax,KD,rmax,rmin}

然后根据式(13)建立评价等级集合。这里采用5级评价等级，即：

V={VP(很差)，P(差)，M(一般),G(好),VG(很好)}

依据表1标准，按照式(14)给出评估矩阵C(r′=2)，战场指挥人员数量为10，根据式(15)求出目标攻击能力的模糊关系矩阵Y1和Y2。

C=[C1C2C3C4C5C6C7]=

Y1=[Y11Y12Y13Y14Y15Y16Y17]=

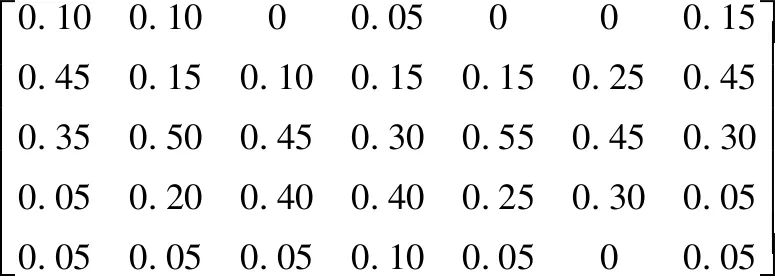
表1 1号导弹能力指标参数

编号KDrmax/kmrmin/kmPhnmaxωmax/(°/s)φm/(°)RTRθRPTRK1m1m211.5200150.8403055150600.8143编号RTIR/kmθIR/(°)PTIRK2θ/(°)WL/mRcs/m2Ave/m2Av/m2Pcdmax/km1100600.9130160.50.330.95100

表2 2号导弹能力指标参数

由式(16)可以求出模糊综合评估模型：

根据式(2)和式(3)求出两种目标的攻击能力分别为：3.683 4和3.418 7。目标其他能力皆按照此法得到，并由此构建目标威力评估矩阵TE

式(1)中指标权重ω1、ω2、ω3分别取0.6、0.2、0.2。利用Matlab对三种不同队形的导弹与目标编队间威力场分布进行仿真。仿真结果见图1～图6。

图1 我方导弹威力场分布 图2 敌方导弹威力场分布

图3 采用横形编队零势线分布 图4 采用楔形编队零势线分布

图5 采用纵形编队零势线分布 图6 不同编队零势线对比效果

图1表示我方导弹编队在战场空间中威力场的分布，图2 表示敌方编队威力场分布。图3～图5分别表示战场空间内横形、楔形和纵形编队零势线分布。需要指出的是，零势线上的点表示双方威力处于均势状态，零势线左下方区域表示我方威力处于优势状态，而零势线右上方区域表示敌方威力处于优势状态。由图6可以直观地看出，当我方采用楔形编队时，我方威力处于优势区域的面积最大，故楔形编队为最佳攻击队形。

4 结论

1) 本文通过引入导弹威力场模型，解决了导弹最佳攻击队形的选择问题。

2) 威力场模型能够较好地将战场态势与导弹性能结合起来，直观描述导弹编队对战场空间每一点的影响，进而呈现作战双方在战场空间中的优势区域。

3) 仿真结果表明，在当前战场态势下，楔形编队具有最佳的攻击效果。在作战双方武器性能差距不大的情况下，选择合适的编队队形对作战效果有一定的提高。