一种基于RBF神经网络的雷达稳定转台复合控制方法

游新望，曹正才

（中国船舶重工集团公司第七二四研究所，南京211153）

0 引 言

舰载雷达常用的两轴稳定系统一般采用基于坐标变换的电子平台技术在方位和俯仰轴上分别对舰船摇摆姿态角（横摇角、纵摇角和航向角）进行实时角度补偿，方位轴完成扇扫、环扫、定位、跟踪等控制功能，俯仰轴确保雷达波束指向保持与大地水平。方位和俯仰闭环控制对象受舰船姿态角影响呈现出明显的非线性和时变不确定性，其速度和加速度皆随舰船姿态角变化而变化，且方位转速越快变化越剧烈［1］。为保证控制精度及控制系统的平稳性，PID控制参数必须根据天线转速及舰船姿态角的变化而实时调整。当天线方位转速范围较宽且舰船姿态角变化剧烈时，PID参数整定难于取得较为理想的控制效果［2］。

PID控制算法由于其结构简单、运算量小、物理意义明确等特点得到了广泛应用。但是，对于那些难以精确取得数学模型的系统，PID控制的参数调整大多是凭经验先比例调节，再积分调节，最后加微分，根据系统的调试效果不断地寻找最合适的数值，反复凑试寻找最优。RBF神经网络是性能优良的前向神经网络，计算量小、学习速度快，在系统辨识和参数估计等有着广泛应用。本文将RBF神经网络与PID控制结合，同时采用前馈或顺馈构成基于神经网络PID的复合控制。实际应用表明，本方法既可保证系统的控制品质，又无需对PID参数进行细分整定，具有较强的实用性［3］。

1 RBF理论及其模型结构

径向基函数（RBF⁃Radial Basis Function） 是 J.Moody和C.Darken于20世纪80年代提出的一种神经网络。它是具有单隐层的3层前馈网络，模拟了人脑中局部调整、相互覆盖接收域的神经网络结构，能以任意精度逼近任意连续函数，输入到输出的映射是非线性的，隐含层到输出的映射是线性的，从而加快了学习速度并避免局部极小问题。RBF神经网络结构如图1所示。

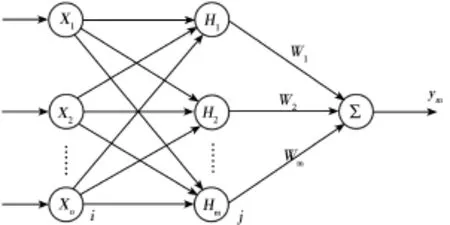
图1 RBF网络模型结构图

在 RBF 网络结构中，X＝［x1，x2，…，xn］T为网络的输入向量。设RBF网络的径向向量H＝［h1，h2，…，hj…，hm］T，其中hj为高斯基函数：

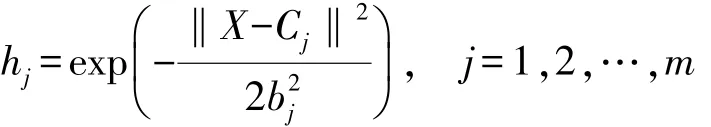
网络的第j个节点的中心矢量为Cj＝［cj1，cj2，…，cji，…，cjn］T，其中，i＝1，2，…，n。

设网络的基宽向量为B＝［b1，b2，…，bm］T，bj为节点j的宽度参数，而且为大于零的数。网络的权向量为W＝［w1，w2，…，wj，…，wm］T，辨识网络的输出为

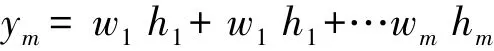
2 RBF网络PID整定

RBF神经网络PID控制结构图如图2所示。控制误差为

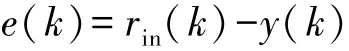
增量式PID控制算法为

整定指标为

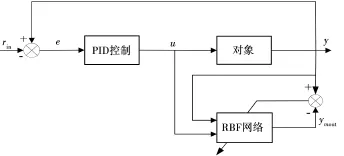
图2 RBF网络整定PID控制框图

式中，kp，ki，kd的调整采用梯度下降法。

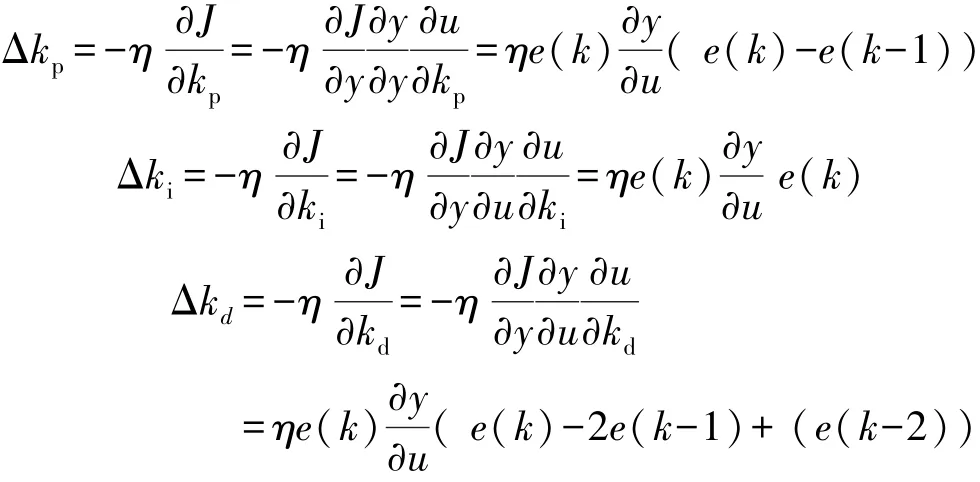
式中，∂y／∂u可通过神经网络的辨识获得。

3 基于RBF网络的雷达稳定转台复合控制

本文以舰载雷达常用的方位和俯仰两轴稳定转台作为被控对象，采用基于RBF网络的复合控制，其中方位控制如图3所示，俯仰控制如图4所示。主闭环控制系统采用基于RBF网络的PID控制器实现反馈控制，其控制参数通过RBF网络的学习功能在线自动整定；采用前馈或顺馈补偿算法进一步降低控制误差，确保控制精度满足要求。

方位和俯仰转台控制采用基于坐标变换的电子平台技术在雷达天线方位和俯仰轴上分别对舰船摇摆姿态角（横摇角、纵摇角和航向角）进行实时角度补偿，从而克服舰船摇摆对雷达系统的不利影响，确保天线轴线的指向精度。其中方位角A和俯仰角E的坐标变换公式如下［4］：

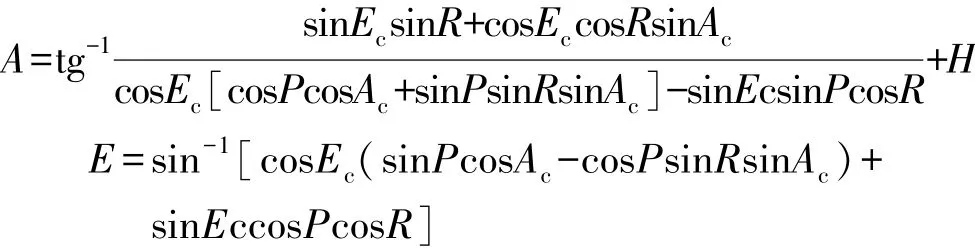
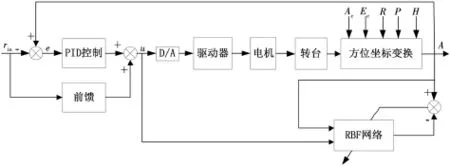
图3 基于RBF网络方位转台复合控制

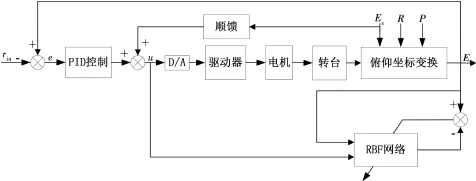
图4 基于RBF网络俯仰转台复合控制

式中，P为甲板平面纵摇角，舰船艏艉线（纵轴）与水平面的夹角，舰艏在水平面上方为正；R为甲板平面横摇角，甲板平面绕舰船艏艉线旋转的角度，右弦下倾为正；H为航向角，从正北开始顺时针到本舰艏方向的夹角，顺时针为正；A为雷达波束方位角，正北与雷达波束指向在水平面投影线的夹角，顺时针为正；E为雷达波束俯仰角，雷达波束指向与其在水平面投影线的夹角，夹角在水平面之上为正；Ac为雷达波束甲板平面方位弦角，舰艏线与雷达波束指向在甲板平面投影线的夹角，顺时针为正；Ec为雷达波束甲板平面俯仰角，雷达波束指向与其在甲板平面投影线的夹角，夹角在甲板平面之上为正。

3.1 方位控制

以某雷达稳定转台为被控对象，舰船摇摆运动条件：横摇±20°、周期 10 s；纵摇±5°、周期 5 s。 以转速30°／s为例，雷达方位控制精度要求均方根误差不大于0.3°。采用基于RBF神经网络的复合控制方法，其闭环控制方位曲线及控制误差如图5所示，PID控制参数Kp、Ki及Kd变化曲线如图6所示。从图5、图6可以看出，PID控制参数随舰船摇摆变化实时调整，方位运动平稳且控制误差较小。经计算得出方位控制误差为 0.212°，满足控制精度要求。

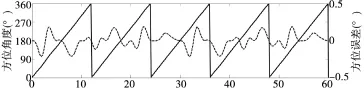
图5 方位曲线及控制误差

3.2 俯仰控制

以某雷达稳定转台为被控对象，舰船摇摆运动条件：横摇±20 °、周期 10 s；纵摇±5 °、周期 5 s。 以转速30°／s为例，雷达俯仰控制精度要求均方根误差不大于0.55°。采用基于RBF神经网络的复合控制方法，其闭环控制曲线及控制误差如图7所示，PID控制参数Kp、Ki及Kd变化曲线如图8所示。从图7、图8可以看出，俯仰控制非线性特征明显，其速度和加速度皆随舰船姿态角及方位指向变化而变化，采用基于RBF神经网络PID控制，PID控制参数随舰船摇摆及方位指向变化而实时调整，俯仰运动平稳且误差控制在合理范围之内。经计算得出俯仰控制误差为0.424°，满足控制精度要求。

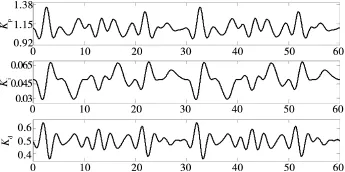
图6 方位控制PID控制参数Kp、Ki及Kd变化曲线

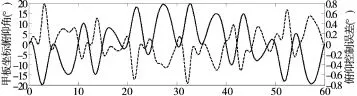
图7 俯仰曲线及控制误差

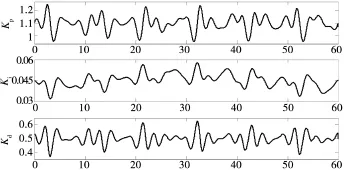
图8 俯仰控制PID控制参数Kp、Ki及Kd变化曲线

4 结束语

从以上的方位、俯仰控制误差曲线可以看出，该控制误差满足某两轴稳定雷达转台闭环控制误差精度要求，并且PID控制参数Kp、Ki及Kd变化曲线随着舰船姿态角变化实时的在线整定，避免了在不同转速及不同海况条件下对PID控制参数进行人工细分整定，具有较强的实用性。

综上所述，利用RBF神经网络在线学习功能，本文采用的基于RBF神经网络PID复合控制方法，实现对控制参数进行在线整定功能，能达到理想的稳定误差稳定精度要求，验证了其应用于两轴稳定雷达转台控制的可行性。