斜侵彻混凝土靶的刻槽弹体的结构响应*

张欣欣，武海军，黄风雷，皮爱国

（1. 北京理工大学爆炸科学与技术国家重点实验室，北京 100081；2. 北京航天微系统研究所，北京 100094）

刻槽弹体在侵彻混凝土的过程中会面临结构稳定性问题。国内外一些学者以自由梁动态结构响应为基础开展了一系列弹体结构稳定性的研究工作。陈小伟[1]以空腔膨胀理论为基础，分析了圆柱壳弹体斜侵彻混凝土的受力情况，针对不同撞击速度的细长中空弹体，分析得到不出现弯曲破坏的弹体最大临界倾角和壳体壁厚下限。皮爱国等[2]基于刚塑形模型和理论载荷分析，给出了弹体在横向和轴向载荷作用下的响应行为，并得到弹体任一截面剪力、弯矩以及轴力的分布规律。王一楠等[3]基于自由梁理论和侵彻阻力分析，给出了小攻角情况下弹体弯曲变形分析。

刻槽弹体作为一种新型结构弹体，在高速侵彻情况下，其锥形弹身可产生恢复力矩，提高弹道稳定性，与此同时，弹身壁厚增加，可提高结构稳定性。本文基于刚塑性理论和侵彻载荷理论分析，将刻槽弹体简化为空间自由变截面梁，给出了弹体在侵彻混凝土早期的刚体响应行为，得到了弹体任一截面弯矩、剪力以及屈服函数的分布规律。基于此理论分析，讨论了刻槽弹体壁厚、材料屈服强度、初速及倾角对弹体弯曲的影响规律。

1 弹体弯曲理论分析

1.1 弹体结构元素计算

刻槽弹体弹身结构如图1所示，在图中坐标系下将分别计算弹体弹身质量、质心及转动惯量等物理量。弹体弹身质量为

式中：m为弹体微元质量，ρ为弹体密度，S(x)为弹体横截面积，表达式为

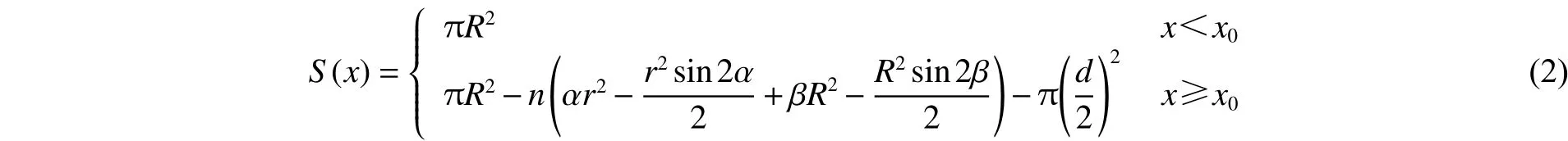
弹体弹身质心为

弹体弹身转动惯量为

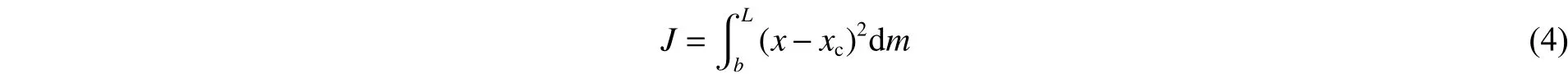
图1 刻槽弹体弹身结构示意图Fig. 1 Illustration of grooved-tapered projectile

1.2 载荷分析

弹体斜侵彻半无限混凝土靶体示意图如图2所示。

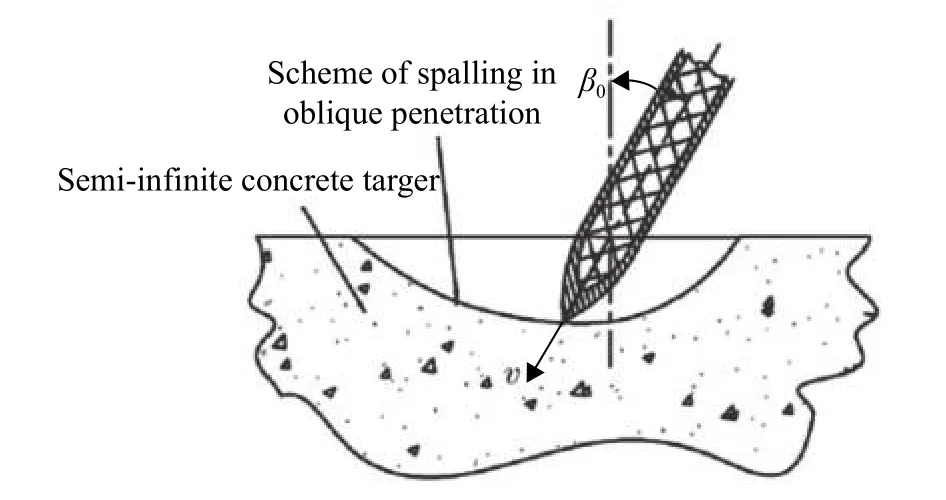
图2 弹体斜侵彻半无限混凝土靶示意图Fig. 2 Illustration of projectile obliquely penetrating the concrete

横向载荷参照陈小伟[1]给出的刚性弹体斜侵彻混凝土靶时的平均侧向作用力

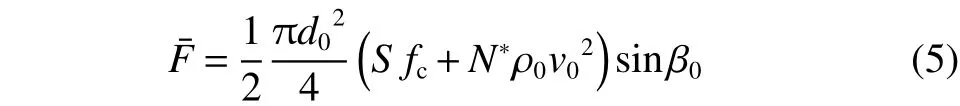
Forrestal等[4]给出的轴向载荷作用力

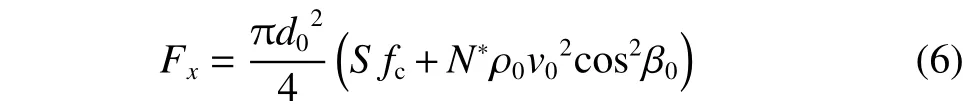
式中：d0为刻槽弹体小端直径；fc为混凝土无约束抗压强度；；ρ0为靶体密度；v0为弹体初速；β0为弹体倾角；N*为弹头形状因子，对于卵形弹头，N*=1/(3ψ)-1/(24ψ2)，ψ 为弹体头部卵形系数。

1.3 弹体弹身各个位置处的剪力和弯矩

塑性铰出现之前弹身刚体运动示意图如图3所示。

图3 刚体运动结构示意图Fig. 3 Illustration of rigid body’s response

在低载情况下，将刻槽弹体简化为变截面自由梁的刚体运动，运动模式如图3所示，将运动分解为绕质心转动和平动，u为端点位移，θ0为端点转角。由刚体动力学可得其运动方程为：

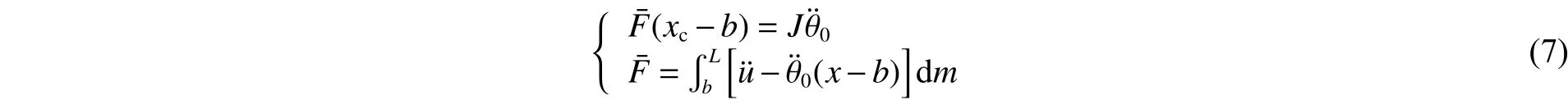
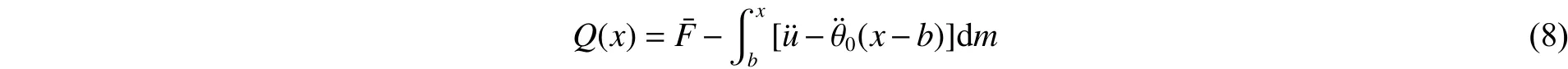
弹身各个位置处的弯矩表达式为：

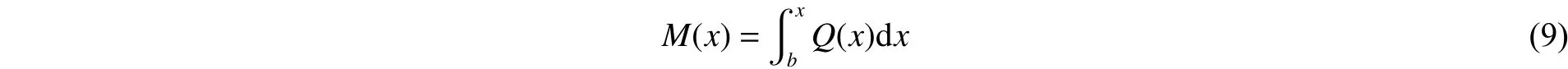
同样采用数值积分法求得弹身各截面位置处的剪力和弯矩分布。

1.4 弹体弹身各个位置处的屈服函数

理想夹层梁弹塑性材料在弹性范围内承受轴力NA和弯矩载荷M共同作用梁截面的屈服条件为[5]：

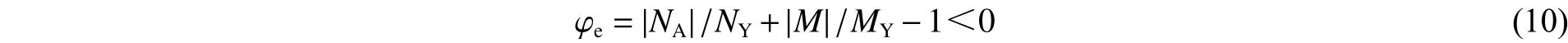
式中：φe为屈服函数，NY及MY分别为截面的分离弹性屈服极限。

针对本文所提刻槽弹体，将各物理参量代入到屈服函数可得：

其中

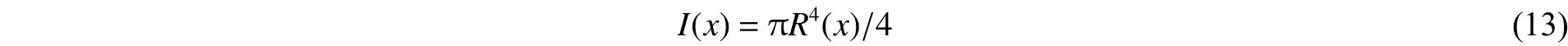
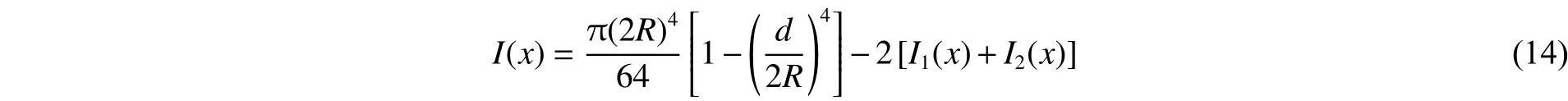
其中

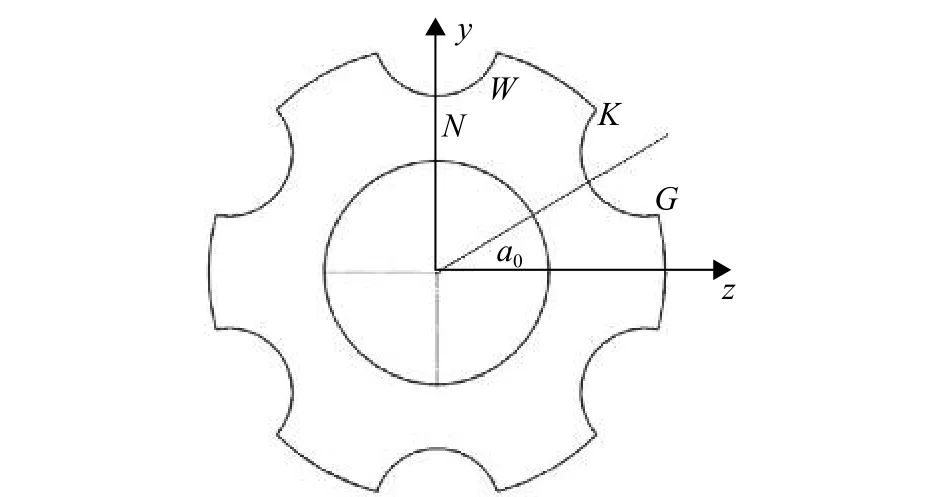
图4 刻槽弹体弹身截面示意图Fig. 4 Illustration of grooved-tapered projectile’s cross section

2 刻槽弹体斜侵彻混凝土结构响应研究

基于1.2节建立的刚塑性分析模型和经过验证合理的轴力弯矩耦合屈服函数[5]，以文献[6]中的刻槽弹体为例，计算斜侵彻工况下弹身各截面剪力和弯矩分布。弹靶结构参数如表1所示。

图7～10分别为不同速度、倾角、弹体内径及弹体材料屈服强度条件下，弹体各截面的无量纲屈服函数。可以看出，对于文中所提刻槽弹体斜侵彻混凝土靶体时的危险截面位于刻槽段的起始截面。由图7可得，随着弹体初速增大，危险截面屈服函数值随之增大，当弹体初速大于1 200 m/s时，危险截面的屈服函数值大于0，表明该处应力已超过弹体材料屈服极限，当作用载荷继续增大时，弹体将发生结构弯曲变形。由图8可得，随着弹体倾角增大，危险截面

屈服函数值随之增大，当倾角大于20°时，危险截面的屈服函数值大于0，表明该截面应力已大于材料屈服强度。由图9可得，随着内径的增大，即壁厚减小，危险截面屈服函数值随之增大，当内径大于22.225 mm时，危险截面的屈服函数值大于0，表明该截面应力已大于材料屈服强度。由图10可得，随着弹体材料屈服强度增大，危险截面屈服函数值随之减小，当屈服强度小于1 500 MPa时，危险截面的屈服函数值大于0，表明该截面应力已大于材料屈服强度。因此，通过本文理论，可计算文献[6]中刻槽弹体在各种条件下保持结构稳定性的临界条件。

表1 弹靶结构参数Table 1 Parameters of the projectile and concrete

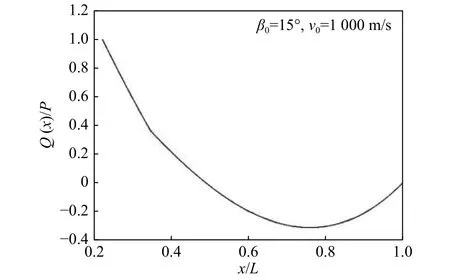
图5 无量纲剪力截面分布Fig. 5 Distribution of dimensionless shearing force

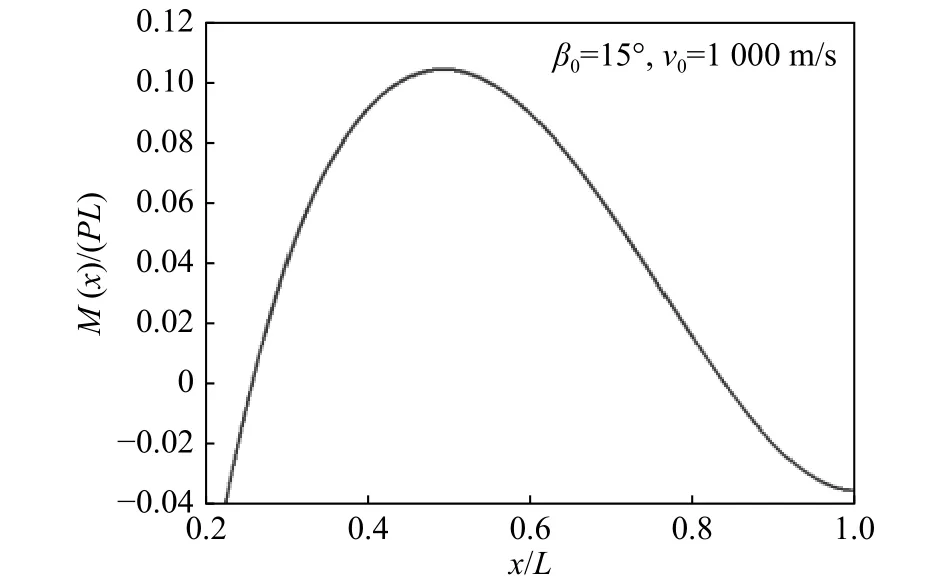
图6 无量纲弯矩截面分布Fig. 6 Distribution of dimensionless bending moment

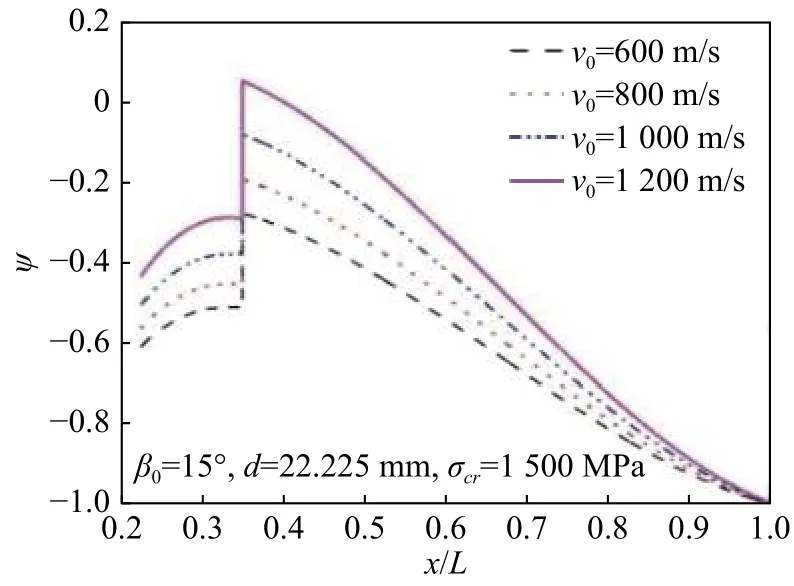
图7 不同速度下的屈服函数Fig. 7 Yield functions at different velocities

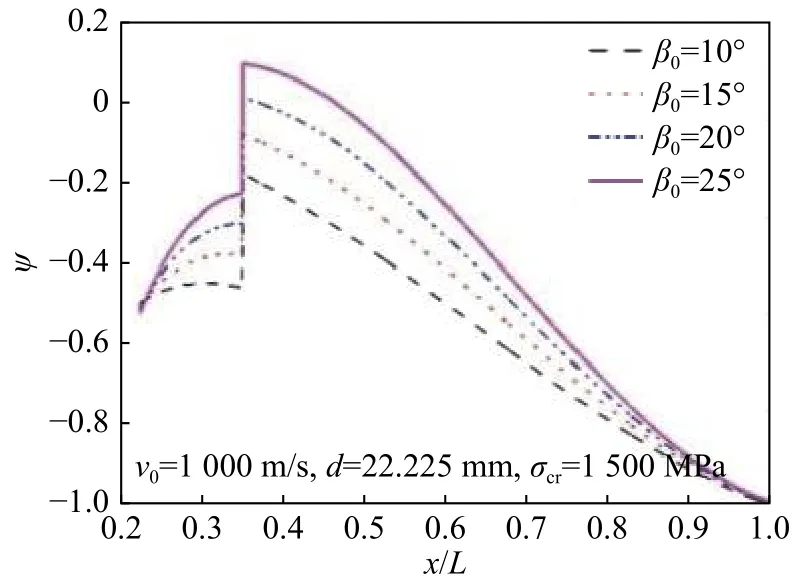
图8 不同倾角下的屈服函数Fig. 8 Yield functions at different obliquities

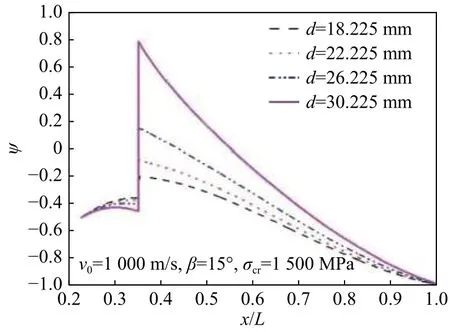
图9 不同内径对应的屈服函数Fig. 9 Yield functions at different inner diameters

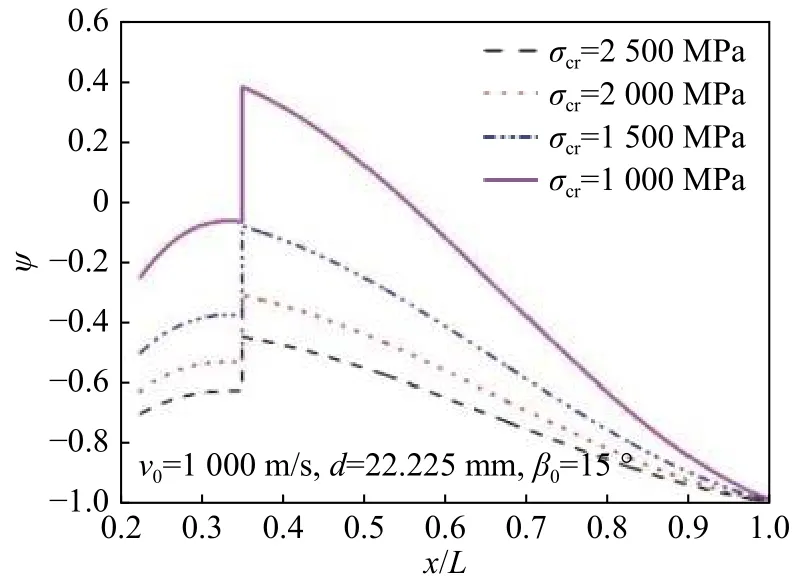
图10 各弹体材料屈服强度下的屈服函数Fig. 10 Yield functions at different yield strength of materials

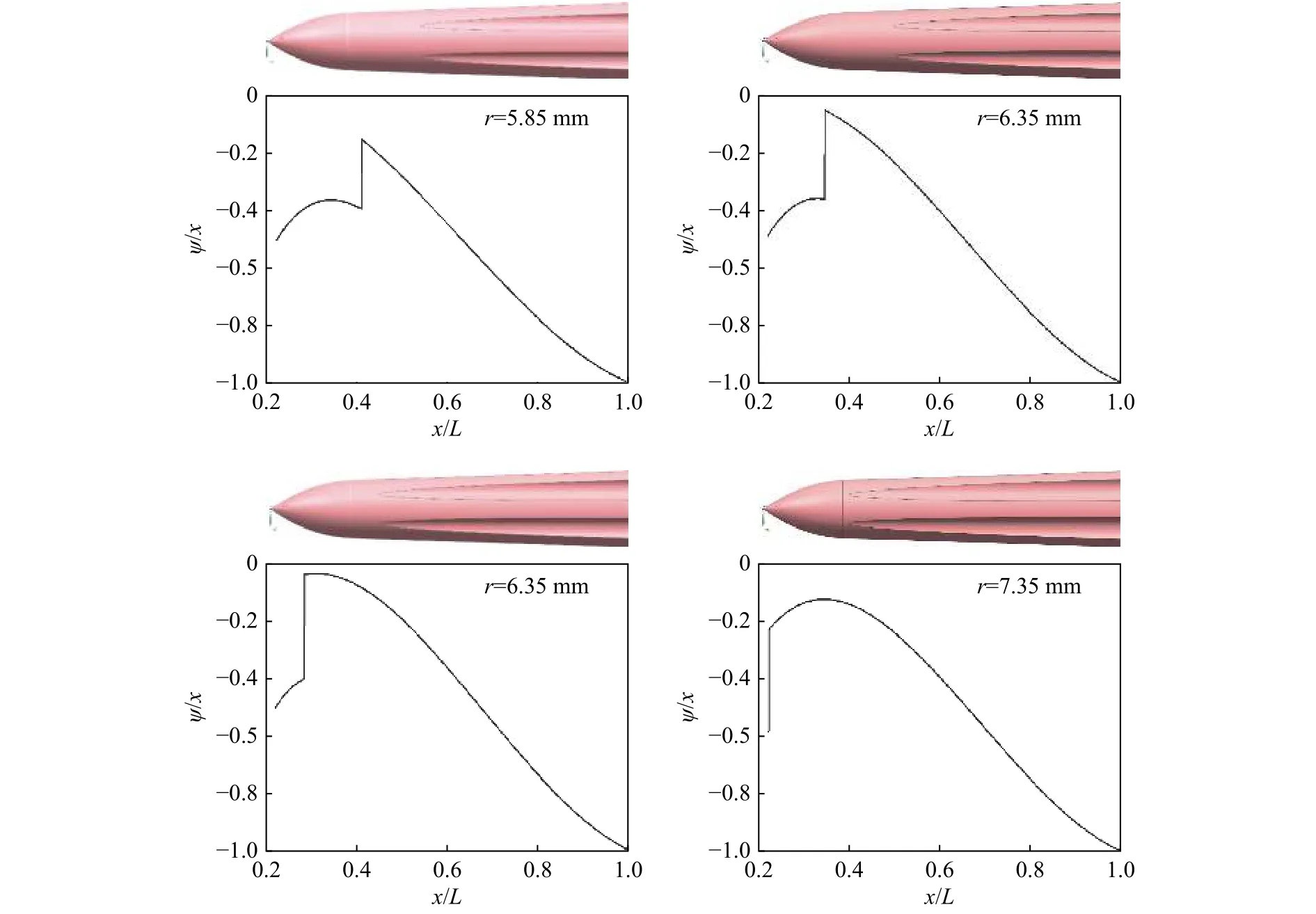
图11 不同刻槽半径的无量纲屈服函数Fig. 11 Yield function at different radii of grooves

由上述计算结果可得，随着刻槽半径的增大，弹体危险截面的屈服函数值也随之增大，当刻槽半径增大到7.35 mm时，危险截面屈服函数值大于0，即弹体发生弯曲；当刻槽半径小于6.85 mm时，弹体的危险截面位于刻槽段起始位置，而当刻槽半径为7.35 mm时，弹体的危险截面向后偏移，位于距弹体头部0.35L处。

3 结 语

基于刚塑性理论和侵彻载荷理论分析，将刻槽弹体简化为空间自由变截面梁，给出了弹体在侵彻混凝土早期的刚体响应行为。对于本文所提刻槽弹体，基于上述理论可计算得到不同条件下弹体不发生弯曲的临界壁厚、材料屈服强度、初速及倾角，同时得到了不同刻槽半径所对应的屈服函数分布规律。