基于HAJIF的大展弦比机翼动力学分析方法研究

李 倩，王立凯，张生贵

（中国飞机强度研究所，陕西 西安 710065）

随着现代航空技术的发展，大展弦比机翼飞机不断涌现，加上先进复合材料在飞机上的广泛运用，飞行器设计中的动力学问题已越来越引起人们的关注。飞机的结构设计除了需要满足规定的功能要求外，也不能忽视结构的使用强度、刚度、稳定性与可靠性。随着飞行器结构强度设计分析技术和试验技术的发展，飞机结构的静力破坏在使用中逐渐减少，而疲劳引起的裂纹和断裂所占的比例明显增多。究其原因，很大一部分是由于振动、冲击等一些动载荷所引起的振动而造成疲劳破坏或动强度破坏[1]。在飞机的实际使用中，由于振动而引起设备、系统的功能失效或降低的事故屡见不鲜。根据国内飞机设计经验，有些构件在设计时强度指标达到要求，运行不久便出现疲劳破坏。通常做法是在哪个部位断裂，就在哪里加固，这种方法不仅增加维护成本自重，而且不能把问题从根本上消除。

结构动力学的发展得益于各种通用型结构动力学分析[2]软件在航空领域的应用，例如 Ansys、Abaqus、MSC/Nastran。这些专业软件兼容性强，内置元素库多，基本上能满足现有动力学分析的所有内容，而且可与各类CAD软件、实体模型生成软件实现无缝对接。然而，这些通用软件由于其通用性，存在和实际工程领域联系不紧密的缺点。值得一提的是，我国也自主研制开发了航空结构强度分析与优化设计软件系统（HAJIF），它是中航工业强度所研制推出的国内航空界功能最为全面的大型CAE软件系统，以强度试验数据库为支撑，提供飞行器结构静强度、动强度、热强度、气动弹性、结构优化设计等基本求解功能，以及飞机结构细节强度校核、耐久性等特色分析功能。系统还提供可满足用户特殊需求的开放式定制环境，并设计有与多种主流CAE软件的接口，具备独立的前后置处理功能。

本文就HAJIF软件中的动力学分析的流程进行详细介绍，对常用特征值分析方法、动力矩阵装配展开具体研究。最后以一个典型的大展弦比机翼为例，对其进行动力学建模与分析，将得到结果与NASTRAN结果对比，验证其正确性。

1  HAJIF 中动力分析的一般流程

动力问题分析的模态法[3]，在选定的频率范围内，把结构的振动模态用作自由度，这就降低了自由度数目而又保持了在该频率范围内的计算精度。在直接法中，自由度仅仅是网格节点的位移。在不同场合下，为了取得最好的效果，结合使用动力问题的模态法和直接法有很重要的意义。在有些问题中，当只需一小部分模态就足以得到理想的精度或者当直接刚度矩阵带宽较大时，采用模态法会更有效。对于直接刚度矩阵（direct stiffness matrix）较小的问题以及有动力耦合，需要较多的振动模态才能获得欲想的计算精度的一些问题，通常采用直接法会更有效。对于非动力耦合问题，亦即对于用模态描述的各种矩阵（matrix of the modal formulation）是对角线的问题，模态法常常会更有效些，尽管计算中需要大量的模态。当然，方法的选择取决于用户。HAJIF中动力分析的一般流程如图1所示。

2  特征值分析

实的与复的特征值分析在HAJIF中是以各自的模块分别执行的，正如图1所示。根据程序的静力学程序所产生的对称的质量矩阵[Maa]和对称的刚度矩阵[kaa]，利用实特征值分析模块READ可获得结构的振动模态，而根据弹性刚度矩阵[kaa]和微分刚度矩阵可获得屈曲模态。所有其它的特征值问题，即具有由其它原因形成矩阵项的特征值问题，其求解用复特征值分析模块CEAD。这样的例子包括有阻尼系统的振动模态，具有气动耦合（aexodynamic coupling）作用的或者具有控制系统之反馈的结构稳定性分析颤振分析以及微分刚度矩阵中具有非对称项的结构屈曲问题。

图1 HAJIF中动力分析的一般流程

用READ求得的特征值可用来形成模态坐标以便进一步用模态法作动力分析。另一方面CEAD的解，也是最后结果。关于实特征值模块与复特征值模块的组织下面分节讨论。

2.1  实特征值分析

用户可以选择两种方法求解屈曲问题，可以选择3种方法求解振动模态问题。HAJIF提供了多种方法以便使不同类型问题的计算效率最佳，同时也是为了弥补万一在特定情况下单独用某种方法所得结果的不足。振动模态特征值问题的一般形式是：

此处，特征值λi=wi2是固有振动频率（natural vibration frequency）的平方。模块执行计算的结果是得到特征值λi和相应于此的经过可供选择的3种方法之一正则化了的特征向量{ai}。据用户的要求，模态质量矩阵按正交模态进行计算和检查：

屈曲特征值问题的一般形式是：

此处特征值λi是载荷因子，乘此因子后的静力载荷条件必将导致屈曲。该模块执行计算的结果是得到特征值λi及相应的特征向量[ai]。对于任何一类特征值问题，用户都必须选择待求的特征值λ的数目或者待求的λ的范围。刚体振动模态用另外一个，由用户指定一组反作用点（支座）ur的程序计算，这样做，是为了改进计算效率，在某些情况下还可改善计算可靠性。在计算其它特征值时，不需要对结构指定这种支座，如果用户没有指定反力点（或者指定的反力点数目不够），则（多余的）刚体模态将要用对有限频率模态（the finite frequency modes）选定的方法进行计算。

与反力点有关的刚体质量矩阵[mr]，以及方程

上式中的变换矩阵[D]都在这套程序的静力部分计算过了，这个方程建立了多余自由度ue和ur的关系。刚体模态是一组向量。

要使方程（15）的乔莱斯基（Cholesky）方程成为可能，必须要求[Maa]是正定矩阵。对于很多问题，[Maa]实际上是奇异的，例如，在转动坐标下当转动惯性可被忽略时就是这样。在这种情况下，如果采用三对角法，为消去最小质量的自由度，必须采取Guyam减缩（Guyam reduction）。

当[C]是三角形矩阵时，其求逆并不难实现。而若网格节点间没有质量耦合也没有推广应用Guyam减缩法时，[C]-1将成为带状矩阵。

实特征值分析模块所执行的最后运算：是要使特征向量正则化；如果用户需要，还要执行质量正交化检查。该检查要求

此处ε是用户提出的，而已被正则化为单位广义质量，即：

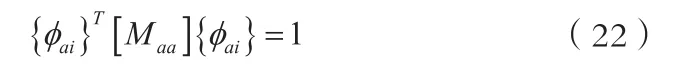
如果检查不合格，则程序将提供检查不合格的成对的模态数目以及对角线外的项之最大值。

应该指出，即使不通过正交化检查，很精确很一致的特征值所对应的特征向量大致上也是精确的。用负幂法（inverse power method）获得的特征向量是相对于所有预先求得的特征值进行正交化的。如果选择的是行列式法（determinant method），则特征值的精确度可以预先检查：

如果一部分相邻的特征值满足精度条件，则正交性检查条件方程（21）就应用于这一部分特征值。经正交性检查不合格的那部分特征向量用史密兹（Schmidt）处理方法进行正交化（orthogonalized）

用户可以要求下述任何一种方式使特征向量正则化（normalization）：

（1）正则化为单位广义质量；

（2）将向量的最大值正则化为单位1；

（3）将向量的一部分分量正则化为单位1。

2.2  复特征值分析

复特征值问题用直接法可表示为：

此处，向量{ud}包括一组结构网格节点上的自由度ud和一组额外节点（extra point）的自由度。质量矩阵[Mdd]，阻尼矩阵[Bdd]和刚度矩阵[kdd]的每一个项都可能是实数或复数，而且这些矩阵可能是对称的或非对称的，奇异的或非奇异的。特征值Pj对应于方程（25）的其次解：

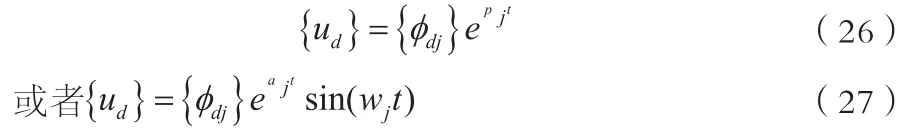
此处aj是pj的实部，wj是pj的虚部。

复特征值问题用模态法可表示为：

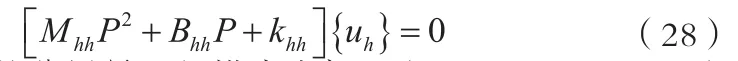
此处{uh}的分量是一组模态坐标ξj（modal coordinates）和一组额外节点的坐标ue，如同直接法一样，不存在对于方程（28）中的矩阵的限制。

提供了两种可供选择的特征值求解法，一种是移位负幂法（the inverse power method），一种是行列式法（determinant method）。

特征值向量正交化，可以使其最大分量的值为1，也可以使由用户选定的某个特定的分量值为1。模态广义质量没有计算，如果可以确定正交性，则正交性检查也不进行。

2.3  动力矩阵装配

动力综合分配器完成若干数据分配。它产生定义各种位移组合中各项的标志，以及内部和外部网格节点数目有关的表格，这个数目包括为了动力分析而明确引入的额外节点数，它形成传递函数数据和特征值求解数据，同时为动力载荷和非线性问题准备表格，并且编辑关于对瞬态分析响应量（reoponre quantities）的明细表。

直接法动力矩阵装配器的功能是要把用不同方法，据节点位移求得的质量矩阵，阻尼矩阵和刚度矩阵装配起来。模态法动力矩阵装配器的功能是对质量矩阵，阻尼矩阵和刚度矩阵实行模态转换。其它执行有关动力分析系统装配功能的模块有包括进行载荷装配的频率响应分析模块和包括进行载荷与运动方程中非线性项装配的瞬态响应分析模块。

3  动力学分析实例

气动弹性计算功能演示验证，采用某型大展弦比机翼为算例，该算例为单边机翼气动外形和结构有限元模型，完成动力学验证计算，图2为某型大展弦比机翼气动力计算模型。选用SINV方法[4]进行模态计算，计算参考尺寸如下：

（1）计算参考点：X=5.040，Y=0.0，Z=0.0。

（2）参考面积：19.0m2。

（3）纵向参考长度：2.0m。

（4）横航向参考长度：20.0m。

有限元模型[5]包括5146个节点，8816个单元，翼面有1个后缘活动舵面（襟、副翼）；蒙皮为复合材料，铺层共16 层：[45°,-45°，0°，90°，0°，45°，-45°，0°]s。 舵 面 为蜂窝结构，面板为复合材料（铺层同蒙皮），蜂芯为全蜂体元。其它为金属材料。机翼有限元模型[6]如图2所示。

图2 机翼动力学计算模型

分别用NASTRAN和HAJIF进行动力学计算并对比，以验证计算的正确性。典型模态如图3和图4所示。

图3 机翼典型模态（NASTRAN计算结果）

图4 机翼典型模态（HAJIF计算结果）

将两个软件的固有频率进行对比，如表1所示。

表1 固有频率对比（Hz）

从以上可以看出，HAJIF的模态求解与NASTRAN相比：

（1）从典型模态变形图可以看出，两者的变形大体一致。

（2）从固有频率可以看出，两者差别不大，HAJIF的计算频率值比NSATRAN整体偏大3.5%左右。

4  结论

本文采用规划法，对一个复合材料机翼，以其结构强度、刚度为约束条件，同时对该机翼的结构尺寸和复合材料铺层进行了优化设计，优化后的机翼结构重量减轻1.4%，同时颤振速度提高5.38%，减重效果明显，性能有所提升。表明本文提出的优化方法有效。

（1）本文介绍了自主国产有限元软件HAJIF的动力学分析方法，给出了详细的特征值数学推导过程。

（2）为了验证分析方法的正确性 ，选用一大展弦比机翼为研究对象，利用商用软件NASTRAN和HAJIF软件分别进行动力学分析，从结果看，两者固有频率较为接近，变形也较为一致。

（3）在优化设计过程中，建立了复合材料铺层库，解决了结构布局与铺层相互影响、相互耦合的问题，实现了单一变量对复杂铺层的表达。该方法还可以应用于其他与复合材料铺层优化相关的问题。