基于改进峭度图法的滚动轴承故障诊断

张海峰 陈丙炎 宋冬利

(1. 中车长春轨道客车股份有限公司国家轨道客车工程研究中心检修研发部，130062，长春； 2. 西南交通大学牵引动力国家重点实验室，610031，成都//第一作者，高级工程师)

滚动轴承广泛应用于旋转机械设备，其健康状态对于旋转设备的正常运行至关重要。为了保证旋转设备，尤其是大型旋转机械设备的持续运转，对滚动轴承进行早期故障检测具有重要意义。

1 轴承故障信号处理方法分析

目前的滚动轴承故障诊断方法多采用振动加速度信号，通过提取故障冲击脉冲信号来识别轴承故障。通常的做法是把脉冲信号分解成一系列由高频到低频的分量，以使一些分量所包含的特征信息更加明显。但是如何提升分解效果，以及如何从分解的分量中选择合适的分量作进一步分析是一个值得研究的问题。

在滚动轴承的故障诊断中，常用峭度来检测故障冲击脉冲信号。最小熵解卷积[1](MED)方法是通过对滤波后的信号进行频谱分析来识别轴承故障及其类型，但是，在强烈背景噪声干扰下，该方法的效果并不是很好。文献[2]提出了谱峭度(SK)，以克服功率谱密度不能有效提取瞬态冲击信号的缺点，该方法是通过计算每一频率成分的峭度来识别非平稳分量，进而确定这些分量所在的频带。后来，文献[3]基于树状滤波器组结构提出了计算谱峭度的快速算法，被称为快速峭度图(fast kurtogram)。快速峭度图的应用效果与基于短时傅里叶变换的峭度图几乎一样，但是计算时间大大减少，极大地推动了它的应用。

为了增强脉冲信号提取能力，文献[4]结合MED和谱峭度来提取轴承故障脉冲信号，并验证了该方法在滚动轴承故障诊断中的有效性。文献[5]结合EMD降噪和谱峭度来提取滚动轴承的早期故障特征，并通过实际工程中的脉冲信号验证了该方法的有效性。

文献[6]认为，基于小波包变换的滤波器组结构能够有效且准确地从嘈杂信号中提取故障特征，并基于小波包变换提出了改进的峭度图。该方法计算小波包分解后各频带信号的峭度，利用峭度最大原则确定共振频带，对共振频带的滤波信号进行频谱分析来识别轴承故障，并通过试验验证了该方法的有效性。文献[7]基于小波包变换提出改进的峭度图，该方法计算小波包分解后脉冲信号包络的相关峭度，根据最大相关峭度确定最优解调频带。相关峭度充分利用了故障信号的周期性，能够很好地检测周期脉冲信号。

针对非高斯噪声和低信噪比对时域峭度影响较大，不能有效识别共振频带的问题，以及考虑到轴承出现局部损伤时包络谱中故障特征频率及其谐波频率处幅值较大的特点，从频域峭度的角度出发，提出了一种改进的峭度图方法。该方法基于树状FIR(有限长单位冲激响应)滤波器组结构，利用特定频带信号包络的功率谱幅值的峭度来量化故障特征，根据峭度最大原则确定最优解调频带信号，然后通过对最优解调频带信号进行频谱分析来识别轴承故障。通过轴承故障仿真信号与实际测试信号对该方法的有效性进行了验证，为滚动轴承的故障诊断提供了一种新的方法。

2 理论方法

2.1 谱峭度和峭度图

文献[3]根据Wold-Cramer表示提出了一个非平稳信号的谱峭度的正式定义。任何零均值非平稳信号x(n)都可以被Wold-Cramer表示，谱峭度被定义为四阶标准累积量。

谱峭度是频率和频率分辨率的函数。基于短时傅里叶变换的谱峭度是频率和窗长度的函数，计算不同频率和窗长度对应的谱峭度并绘制在分别以频率、窗长度为横坐标和纵坐标的二维图中就得到最初的峭度图。为了减少获得峭度图的计算时间，文献[3]提出了基于树状多速率滤波器组结构的快速算法。该算法采用1/3-二叉树结构，可以划分更多的频带，能够更加准确地识别共振频带。快速峭度图的具体算法如下。

(1)构造一个截止频率为fc=1/8+ε(ε>0，所有频率为归一化频率，采样频率fs归一化为1)的低通原型滤波器h(n)，然后基于h(n)构造一个准解析低通滤波器h0(n)和一个准解析高通滤波器h1(n)，频带分别为[0,1/4]、[1/4,1/2]。

(1)

式中：

j——虚数单位；

n——滤波器系数的序号。

(2)对第k层分解得到的第i个的系数序列ck,i(n)分别进行h0(n)低通滤波和h1(n)高通滤波，对滤波结果做2倍降采样得到第k+1层的2个子系数序列ck+1,2i(n)和ck+1,2i+1(n)。i=0，1，…，2k-1；k=0，1，…，K-1；c0(n)为原始信号。需要注意的是，在高通滤波之后，滤波后的序列要乘以(-j)n转换成低通序列。

(3)构造3个准解析带通滤波器gr(n)，r=0，1，2，通带分别为[0,1/6]，[1/6,1/3]，[1/3,1/2]。这些滤波器用于进一步把序列ck,i(n)分解成3个子序列ck.6,i+r(n)(下标k.6为非整数，表示第k.6层)，分别对应频带[i·2-k-1,(i+1)2-k-1]的低、中、高频部分，并对滤波结果做3倍降采样。按照此过程对原始信号x(n)进行K层分解，最终得到一系列系数序列。

(4)由滤波器组分解得到的系数序列ck,i(n)就是信号x(n)对应于中心频率fi=(i+2-1)2-k-1和带宽(Δf)i=2-k-1的复包络。根据式(2)计算所有系数序列ck,i(n)的峭度，进而就可以得到快速峭度图。式(2)中，i=0，1，…，2k-1，k=0，1，…，K-1；〈·〉是平均运算符，|·|是求模运算符。

(2)

2.2 功率谱

功率谱可以通过参数或非参数方法计算。在非参数方法中，常采用自相关函数的傅里叶变换和部分平均法估计功率谱。时域连续信号x(t)的自相关函数为：

(3)

自相关函数是延迟时间τ的函数，是原信号与延迟后信号之间相似性的度量。对自相关函数Rx(τ)作傅里叶变换即可得到功率谱S(f)。

(4)

式中：

f——频率。

3 基于改进峭度图的滚动轴承故障诊断

轨道交通车辆轴承振动信号通常混有强烈的背景噪声，这大大增加了故障信号的提取难度。谱峭度及峭度图凭借其有效的脉冲信号提取能力在旋转轴承的故障诊断中得到了广泛应用。但时域峭度容易受到低信噪比和非高斯噪声等不利条件的影响，会导致谱峭度和峭度图方法不能准确识别共振频带，最终导致无法有效提取故障特征。

在滚动轴承正常情况下，其振动信号的功率谱幅值在整个频率范围内均匀分布，由功率谱计算得到的峭度一般较小。但轴承出现局部损伤时，其振动信号的功率谱中轴承故障特征频率及其谐波频率处就会出现幅值较大的峰值，此时由功率谱计算得到的峭度很大。此外，振动信号中的背景噪声通常包含大量的频率成分，如果把时域的背景噪声转换到频域，背景噪声就会均匀分布在整个频率范围内，有效避免了非高斯噪声对峭度的影响。基于此，提出了一种改进的峭度图方法，计算由1/3-二叉树滤波器组分解得到的特定频带信号包络的功率谱幅值的峭度，再根据峭度最大原则确定共振频带，然后通过对共振频带的滤波信号进行频谱分析来识别轴承故障。基于改进峭度图的滚动轴承故障诊断流程如图1所示。

图1 基于改进峭度图的滚动轴承故障诊断流程

4 仿真数据分析

4.1 轴承振动信号仿真模型

为了验证改进的峭度图方法在滚动轴承故障诊断中的有效性，建立了轴承振动信号仿真模型，由振动仿真模型得到轴承不同零件故障时的仿真信号。轴承故障仿真信号x(t)可以表示为：

x(t)=c1(t)+c2(t)+c3(t)+n(t)

(5)

式中：

t——表示时间；

n(t)——背景噪声，常用高斯分布白噪声模拟；

c1(t)——滚动轴承局部故障激起的脉冲信号，可用式(6)表示；

c2(t)——其他零部件撞击轴承而产生的冲击脉冲或电磁干扰，可用式(7)表示；

导致继续医学教育管理问题的成因和影响矛盾变化的因素十分复杂，如何减少甚至化解存于其中的问题是值得研究的系统工程，以下将针对管理问题提出教育应该做到如何的改革和调整，以实现优化人才配置和专业设置的合理性，希望对于我国教育行业的稳定持续发展提供相关的理论参考。

c3(t)——来自转轴转动、啮合等的离散谐波干扰，可用式(8)表示。

(6)

式中：

M——故障脉冲数量；

T——相邻两个脉冲出现的时间间隔；

τi——轴承零件之间相对滑动引起的时间延迟，通常为时间间隔Ta的1%～2%；

Ai——用来模拟振动信号的幅值调制(只在轴承内圈故障和滚动体故障中存在)；

fa——由冲击激起的共振频率；

φa——故障脉冲的相位；

(7)

式中：

N——未知(随机)脉冲数量；

Tj——第j个脉冲的发生时间；

Bj——第j个脉冲的幅值；

Db——随机脉冲的共振衰减系数；

fb——由随机脉冲激起的共振频率；

φb——随机脉冲的相位。

(8)

式中：

R——干扰分量的个数；

Ck——第k个干扰分量的幅值；

fk——第k个干扰分量的频率；

βk——第k个干扰分量的相位。

4.2 轴承外圈故障仿真分析

为了模拟滚动轴承外圈局部损伤时的振动加速度信号，设置轴承外圈故障特征频率fo=1/T=为59 Hz(下标o表示轴承外圈，此处的fo即为式(6)中的fa)，采样频率fs为12 000 Hz，由外圈局部故障激起的共振频率fa为4 800 Hz，数据长度为24 000个采样点。振动信号仿真模型中其他参数设置为M=1 000，N=3，Ai=1，φa=0，Da=1 000，随机脉冲激起的共振频率fb=2 000 Hz，随机脉冲的共振衰减系数Db=800，随机脉冲的相位φb=0，τi用[0.01Ta,0.02Ta]范围内服从均匀分布的随机数表示，R=2，C1=C2=0.025，f1=7 Hz，f2=13 Hz，β1=π/6，β2=-π/3。背景噪声n(t)采用均值为0、方差为0.4的服从正态分布的高斯白噪声。由轴承振动信号仿真模型得到的外圈故障仿真信号如图2所示。

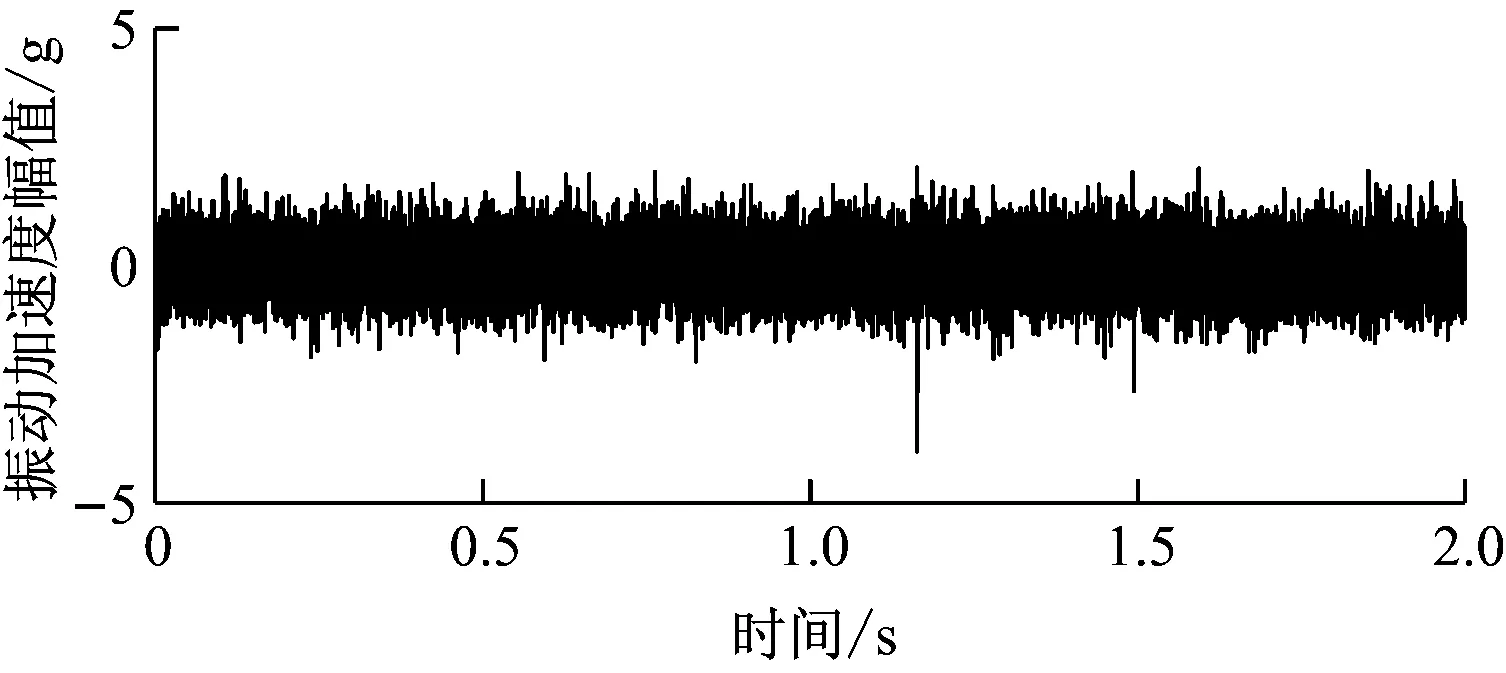
图2 轴承外圈故障仿真信号

由图2可以看出，外圈故障脉冲信号淹没在强烈的背景噪声中，并且出现有幅值非常大的随机脉冲信号。采用改进的峭度图方法对轴承外圈故障仿真信号进行处理后得到的峭度图如图3所示。由图3可知，最优解调频带的带宽(Bw)为375 Hz，中心频率Fc为4687.5 Hz，与设置的共振频率4 800 Hz非常接近。根据共振频带得到的解调信号的包络谱如图4所示。由图4可以清楚地看出前5阶轴承外圈故障特征频率。因此可知，改进的峭度图方法准确识别了共振频带，并且有效地提取出了外圈故障特征信号。

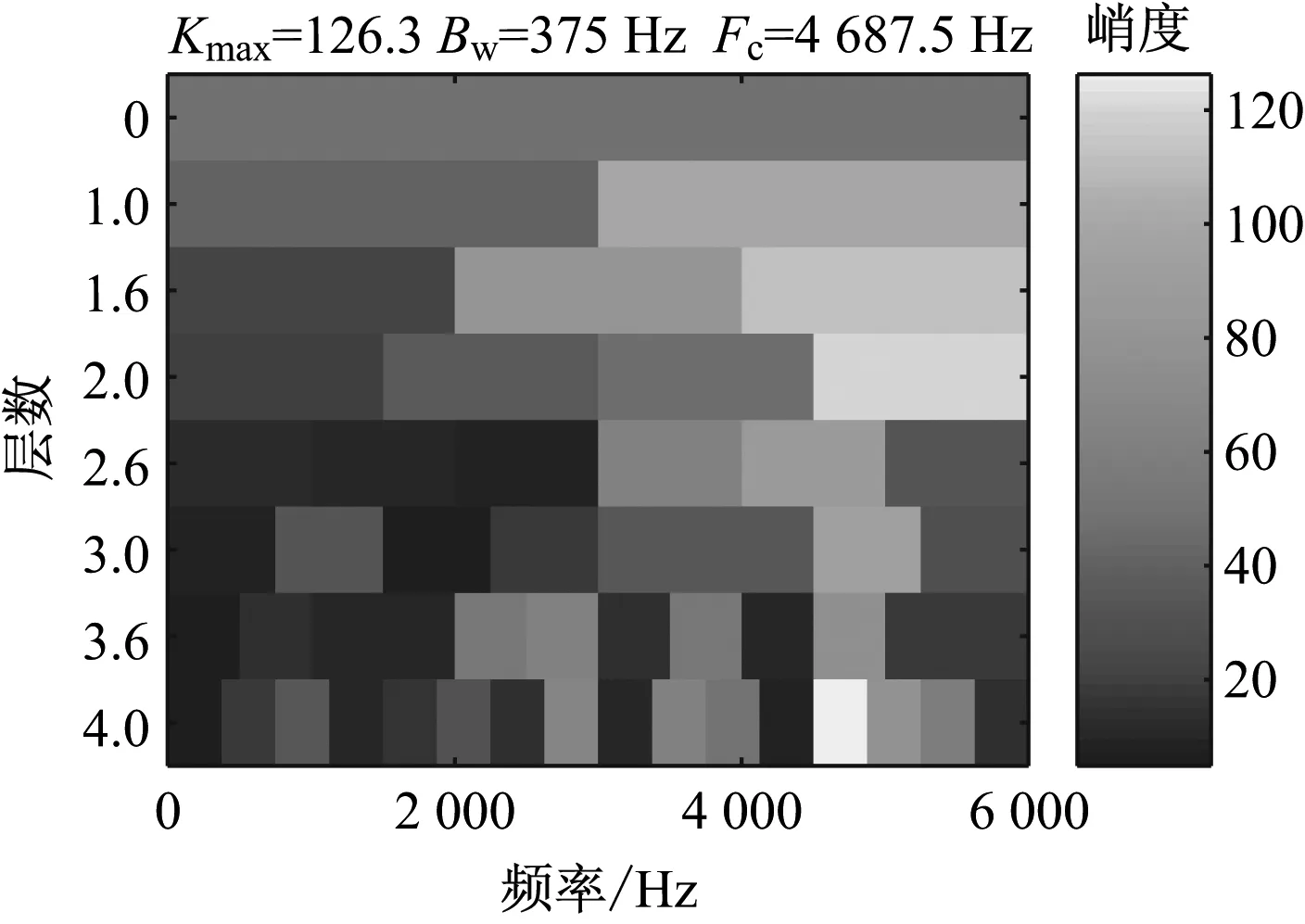
图3 采用改进峭度图法对轴承外圈故障仿真信号处理后的峭度图

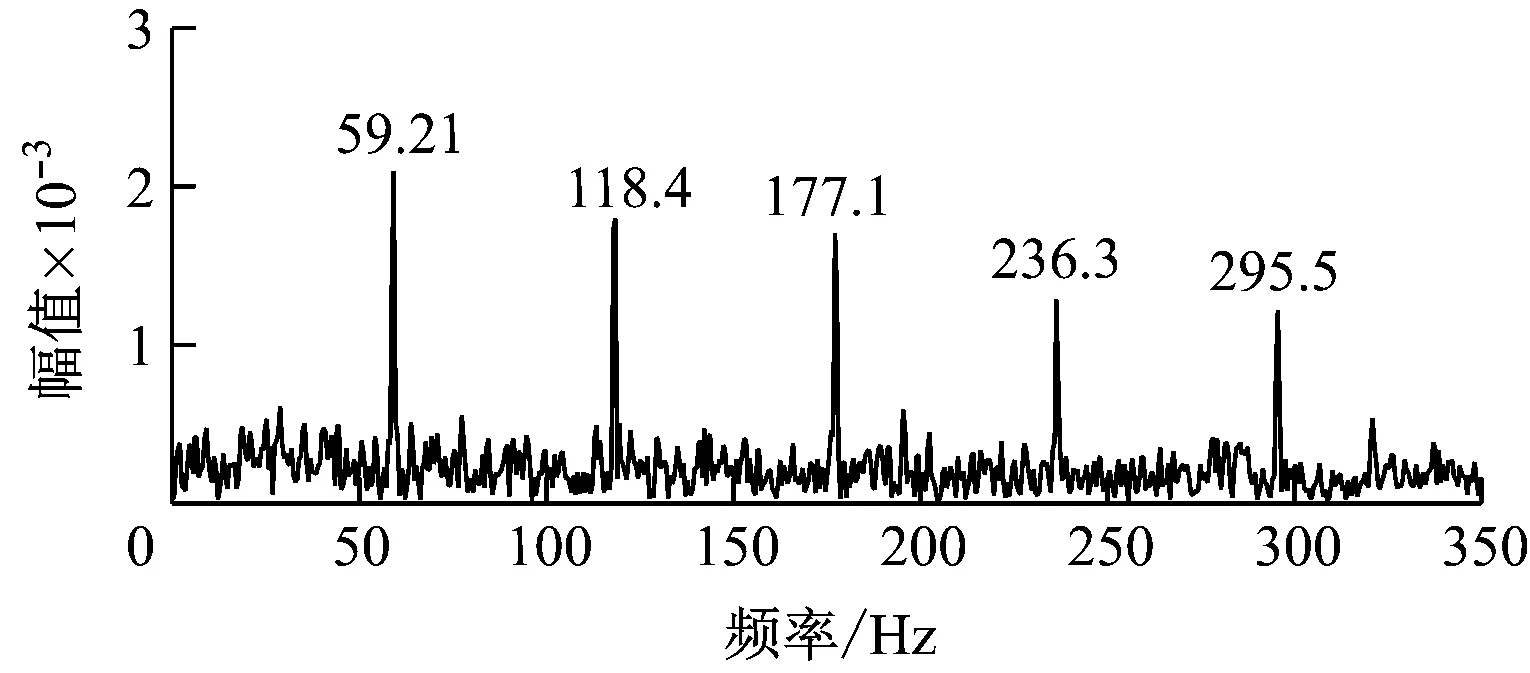
图4 采用改进峭度图法的轴承外圈解调信号包络谱

采用快速峭度图法对轴承外圈故障仿真信号进行处理后得到的峭度图如图5所示。由图5可知，最优解调频带的带宽为500 Hz，中心频率为2 250 Hz，与设置的共振频率4 800 Hz相差很远。根据解调频带得到的滤波信号的包络谱如图6所示。由于受到强烈背景噪声和随机脉冲信号的影响，快速峭度图法未能准确找到共振频带，从而没能有效提取出外圈故障特征信号，最终导致包络谱中故障特征频率非常不明显。

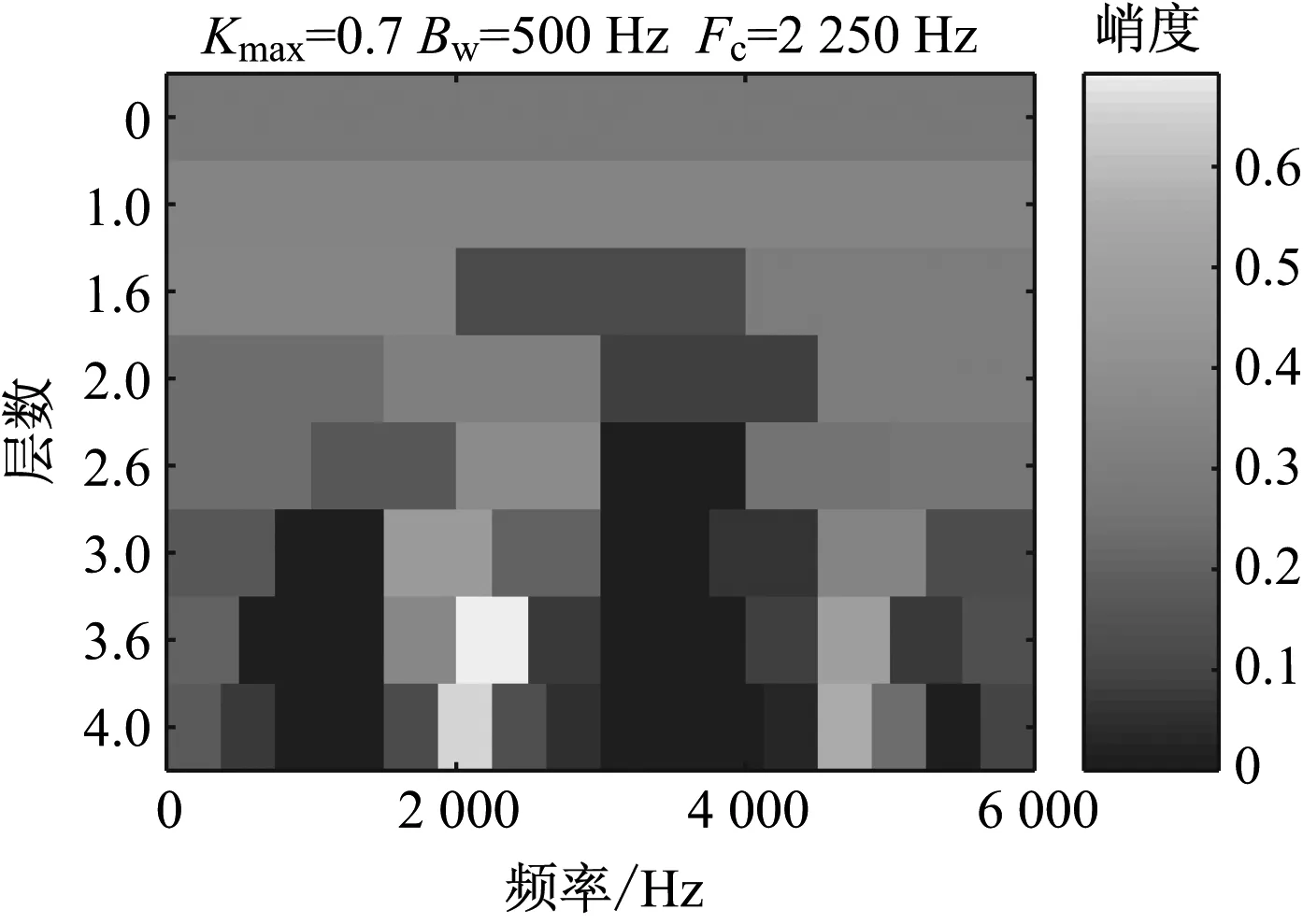
图5 采用快速峭度图法对轴承外圈故障仿真信号处理后的峭度图

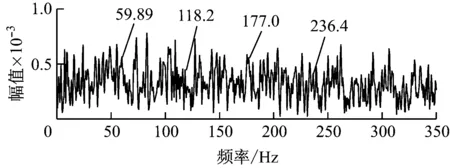
图6 采用快速峭度图法的轴承外圈解调信号包络谱

4.3 轴承内圈故障仿真分析

设置轴承内圈故障特征频率fi也为59 Hz，轴承内圈旋转频率fr为10 Hz，由内圈局部故障激起的共振频率fa为1 700 Hz，幅值调制Ai=0.5[1-sin(2πfrt)]，其他参数设置与轴承外圈故障仿真信号模型的参数设置相同。

由仿真模型得到的轴承内圈故障仿真信号如图7所示。由图7可以看出，内圈故障脉冲信号淹没在了强烈的背景噪声中，并且有非常明显的未知干扰脉冲。用改进的峭度图方法对内圈故障仿真信号进行处理后得到的峭度图如图8所示。由图8可知，最优解调频带的带宽为3 000 Hz，中心频率为1 500 Hz，与设置的共振频率1 700 Hz非常接近。根据解调频带得到的解调信号的包络谱如图9所示。由图9可以清楚地看出前5阶轴承内圈故障特征频率，并且该频率受到了内圈旋转频率的调制。因此可知，改进的峭度图法准确识别了共振频带，并有效地提取出了内圈故障特征信号。

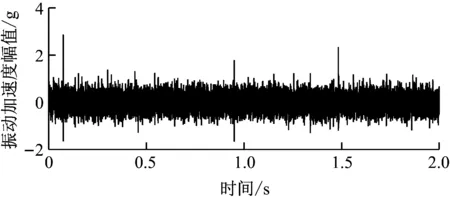
图7 轴承内圈故障仿真信号

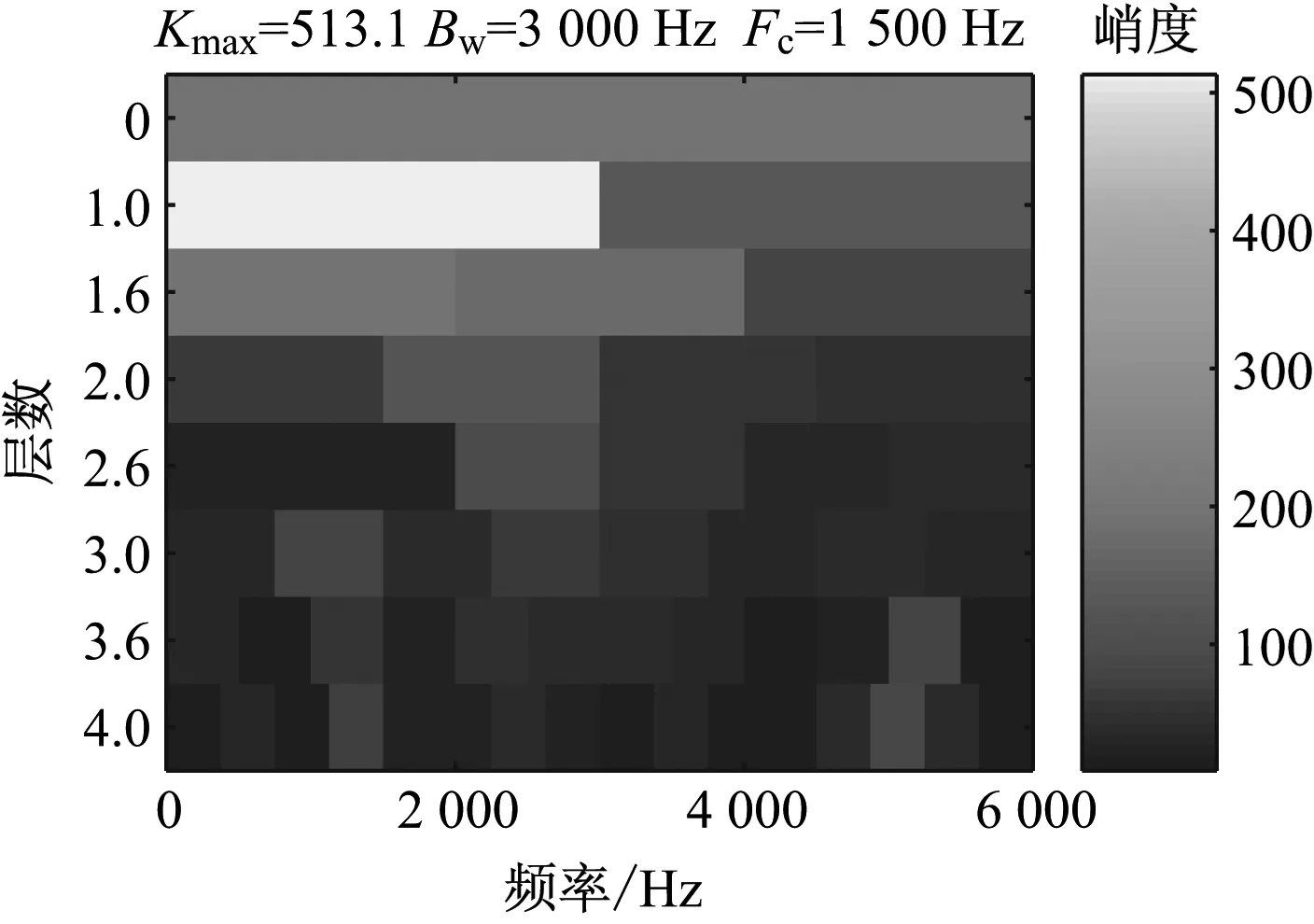
图8 采用改进峭度图法对轴承内圈故障仿真 信号处理后的峭度图

图9 采用改进峭度图法的轴承内圈解调信号包络谱

采用快速峭度图方法对轴承内圈故障仿真信号进行处理后得到的峭度图如图10所示。由图10可知，最优解调频带的带宽为500 Hz，中心频率为2 250 Hz，与设置的共振频率1 700 Hz相差较大，并且最优频带不包含共振频率。根据解调频带得到的滤波信号包络谱如图11所示。由于强烈噪声和峰值较大的随机脉冲信号的干扰，快速峭度图未能准确识别共振频带，以至于未能有效提取出内圈故障特征信息，最终导致包络谱中相应的故障特征频率及其谐波不明显。

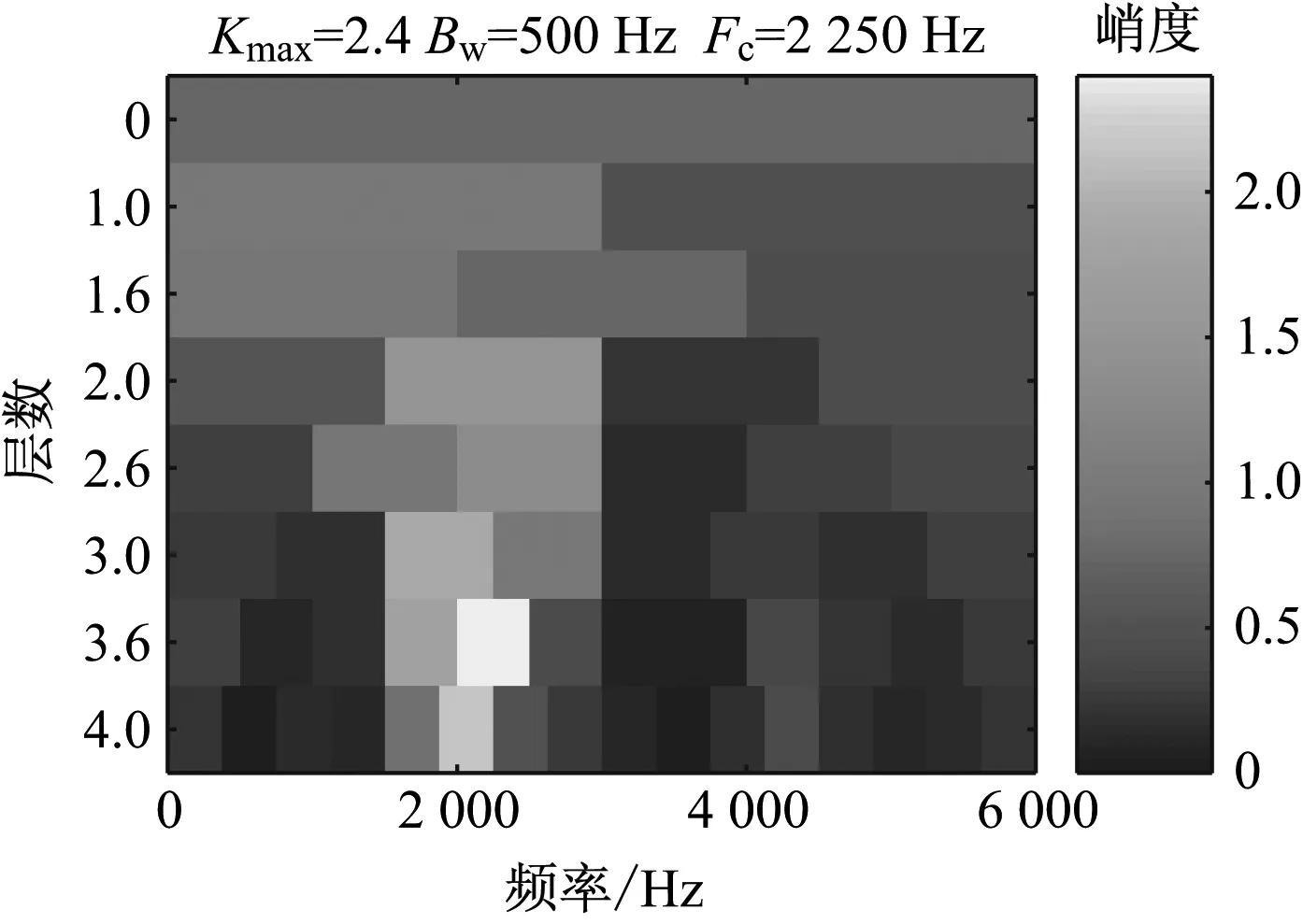
图10 采用快速峭度图法对轴承内圈故障仿真 信号处理后的峭度图

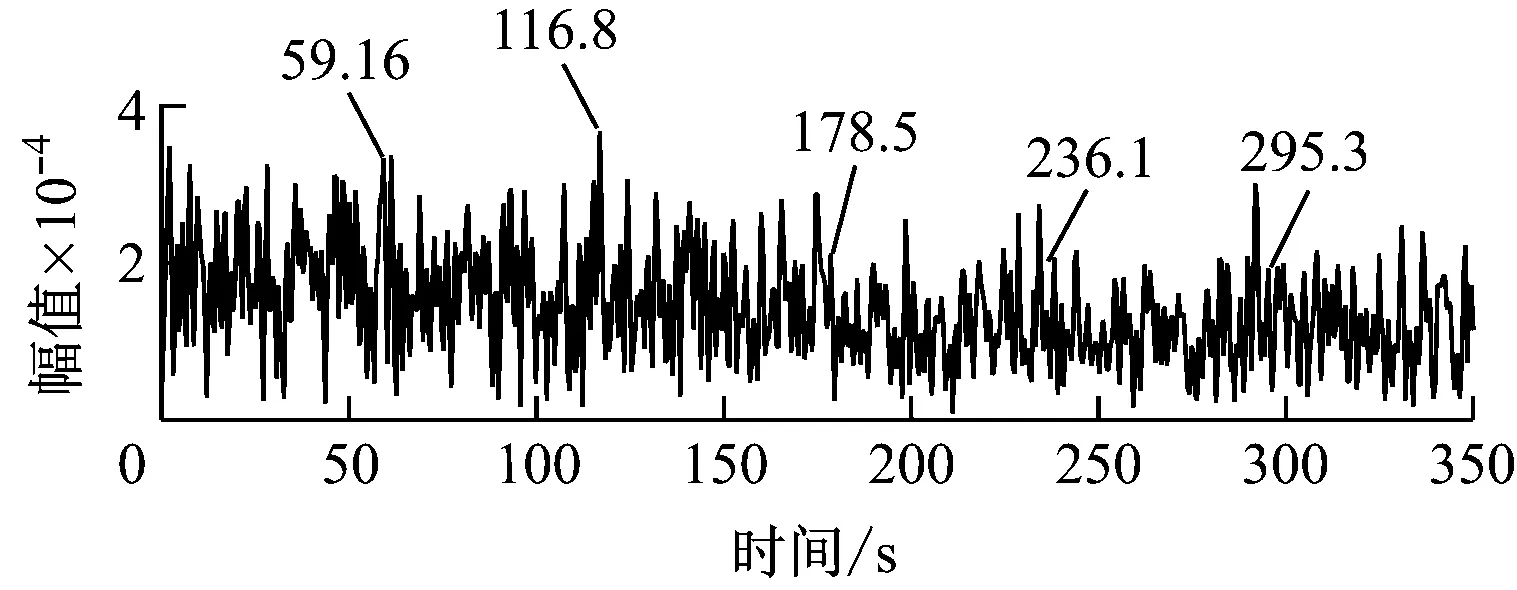
图11 采用快速峭度图法的解调信号包络谱

5 试验数据分析

为了验证改进的峭度图方法在实际轴承故障诊断中的有效性，利用滚动轴承试验台分别采集轴承外圈局部故障和滚动体局部故障时的振动加速度信号。采样频率为12 800 Hz，振动加速度信号的长度为8 192个采样点。装有齿轮的转轴两端通过轴承支撑在轴承座中，电机通过联轴器驱动转轴旋转。

5.1 轴承外圈故障试验数据分析

由试验台得到的轴承外圈故障振动加速度信号(试验信号)如图12所示。由图12可见，故障脉冲信号受到噪声干扰但不明显。采集加速度信号时电机转速为595 r/min，根据转轴转速和轴承尺寸参数计算得到轴承外圈故障特征频率为72.4 Hz。用改进的峭度图法对试验信号处理后得到的峭度图如图13所示。由图13可知，最优解调频带的带宽为3 200 Hz，中心频率为4 800 Hz。根据最优解调频带得到的解调信号包络谱如图14所示，从图14中可以清楚地看出前4阶轴承外圈故障特征频率。因此可知，改进的峭度图法识别了共振频带，并有效地提取出了外圈故障特征信息。

图12 轴承外圈故障试验信号

图13 采用改进峭度图法对轴承外圈故障试验 信号处理后得到的峭度图

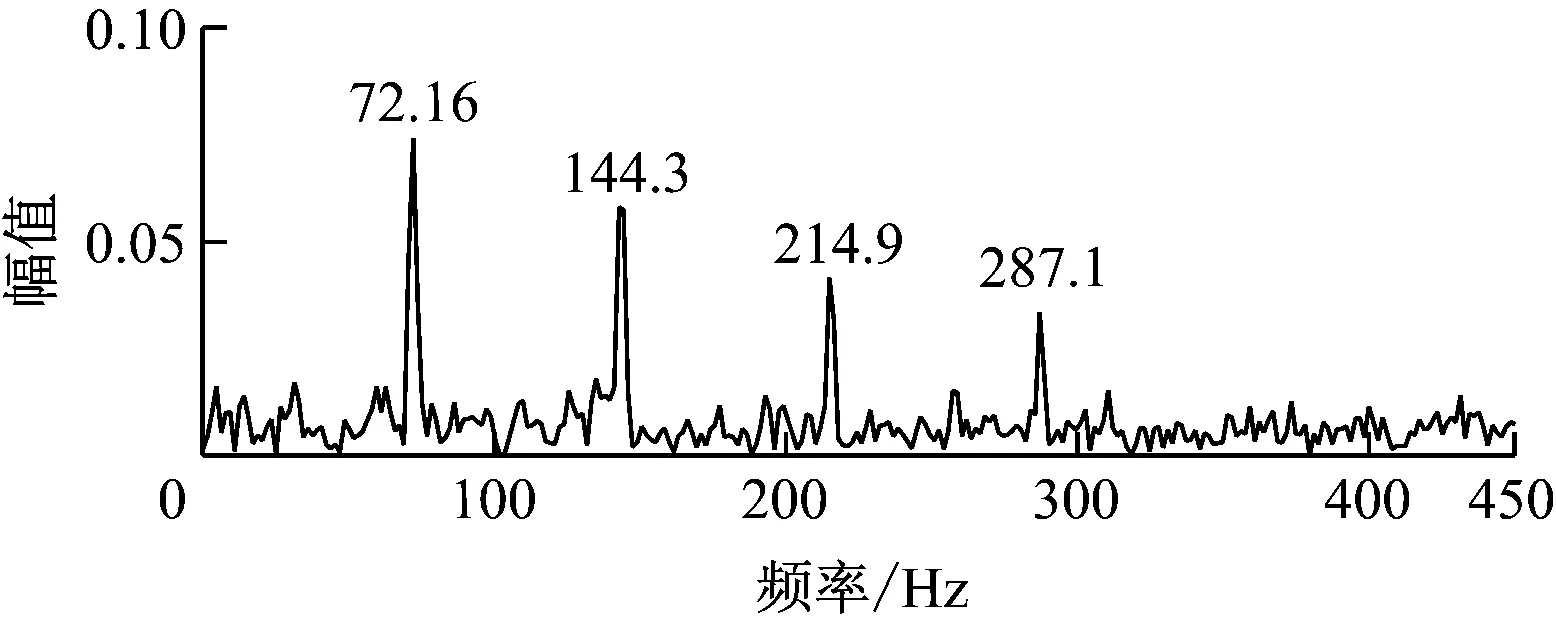
图14 采用改进峭度图法的轴承外圈解调 信号包络谱(试验)

采用快速峭度图法对轴承外圈故障试验信号进行处理后得到的峭度图如图15所示。由图15可见，最优解调频带的带宽为2 133 Hz，中心频率为1 067 Hz。由解调频带得到的解调信号包络谱如图16所示。由图16可见，在包络谱中，很难识别轴承外圈故障特征频率及其谐波频率。由此可知，快速峭度图法未能准确识别共振频带，从而无法有效提取出外圈故障特征信息，最终导致包络谱中故障特征频率及其谐波非常不明显。

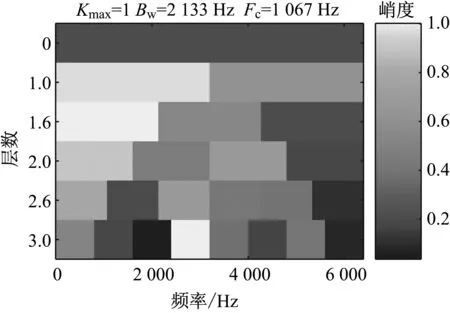
图15 采用快速峭度图法对轴承外圈故障试验 信号处理后得到的峭度图

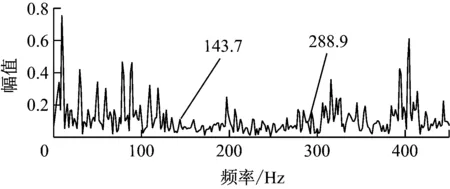
图16 采用快速峭度图法的轴承外圈解调 信号包络谱(试验)

5.2 轴承滚动体故障试验分析

为进一步验证改进峭度图法对提取轴承故障特征信息的有效性，利用试验台获取轴承滚动体故障振动加速度信号(试验信号)，如图17所示。由图17可见，故障脉冲信号受到噪声干扰，因而很难被识别。采集信号时电机转速为855 r/min，根据转轴转速和轴承尺寸参数计算得到轴承外圈故障特征频率为48.4 Hz。

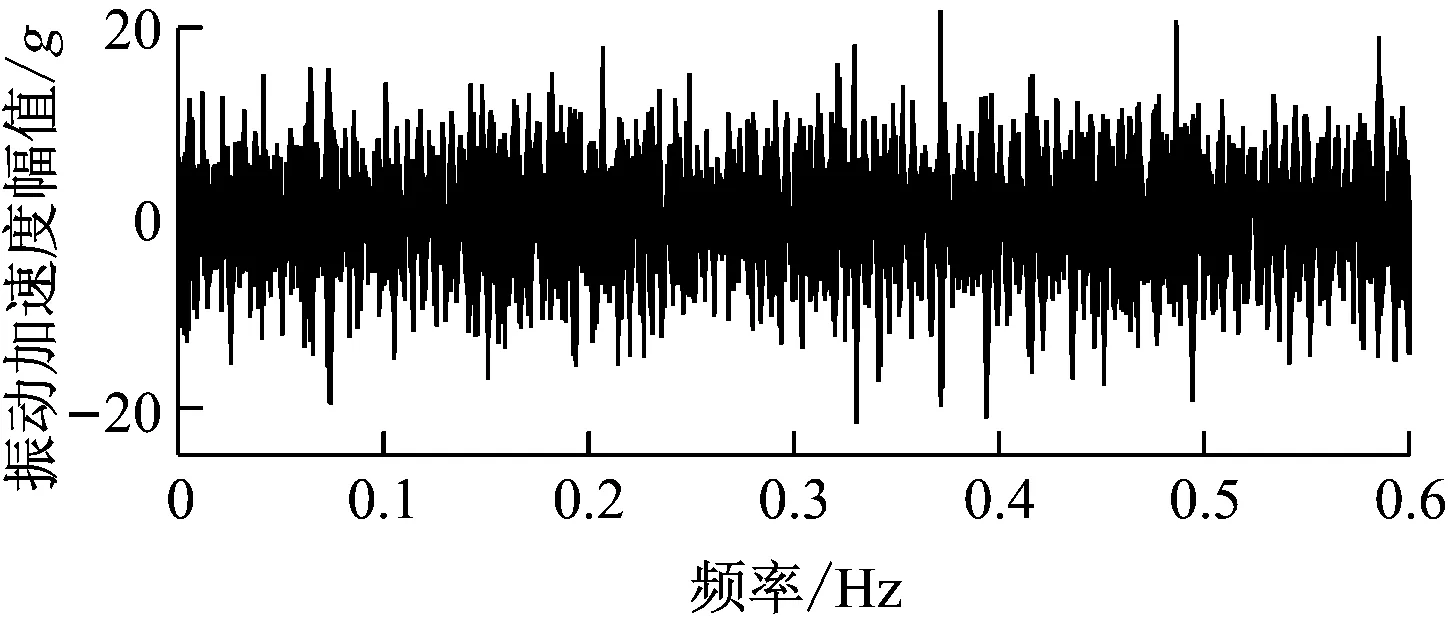
图17 轴承滚动体故障试验信号

用改进的峭度图法对轴承滚动体故障试验信号处理后得到的峭度图如图18所示。由图18可见，最优解调频带的带宽为2 133 Hz，中心频率为5 333 Hz。根据解调频带得到的解调信号包络谱如图19所示。由图19可见，在包络谱中，可以清楚地看出前4阶滚动体故障特征频率，并且该频率受到了保持架旋转频率的调制。由此可知，改进的峭度图法有效提取出了滚动体故障特征信息。

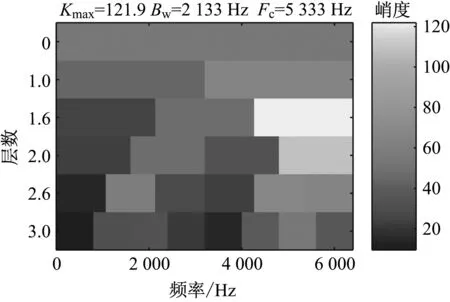
图18 采用改进的峭度图法对轴承滚动体故障 试验信号处理后得到的峭度图

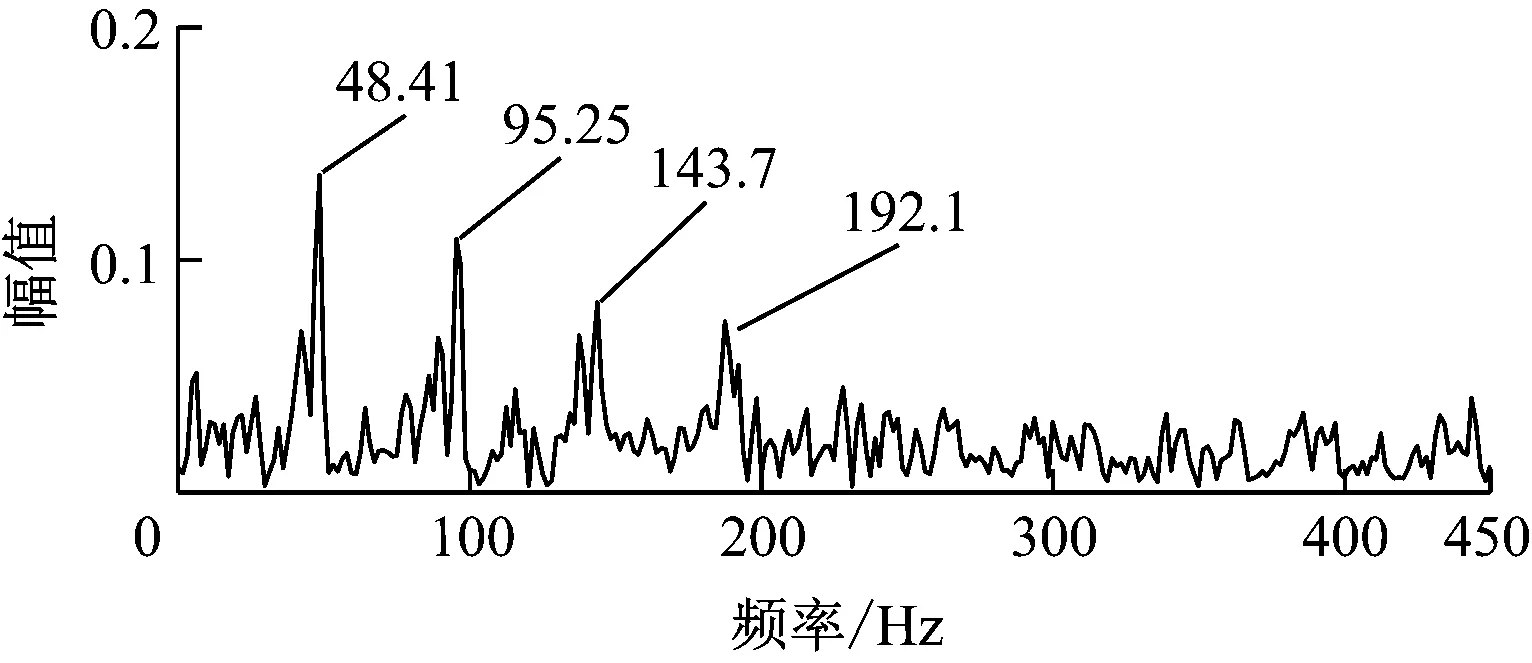
图19 采用改进峭度图法的轴承滚动体解调信号包络谱

采用快速峭度图法对轴承滚动体故障试验信号进行处理后得到的峭度图如图20所示。由图20可见，最优解调频带的带宽为1 067 Hz，中心频率为4 800 Hz。由解调频带得到的解调信号的包络谱如图21所示。由图21可见，在包络谱中，前两阶轴承滚动体故障特征频率比较明显，但后两阶特征频率由于受到保持架旋转频率的调制而不明显。由此可知，快速峭度图方法未能充分提取轴承滚动体故障特征信息。

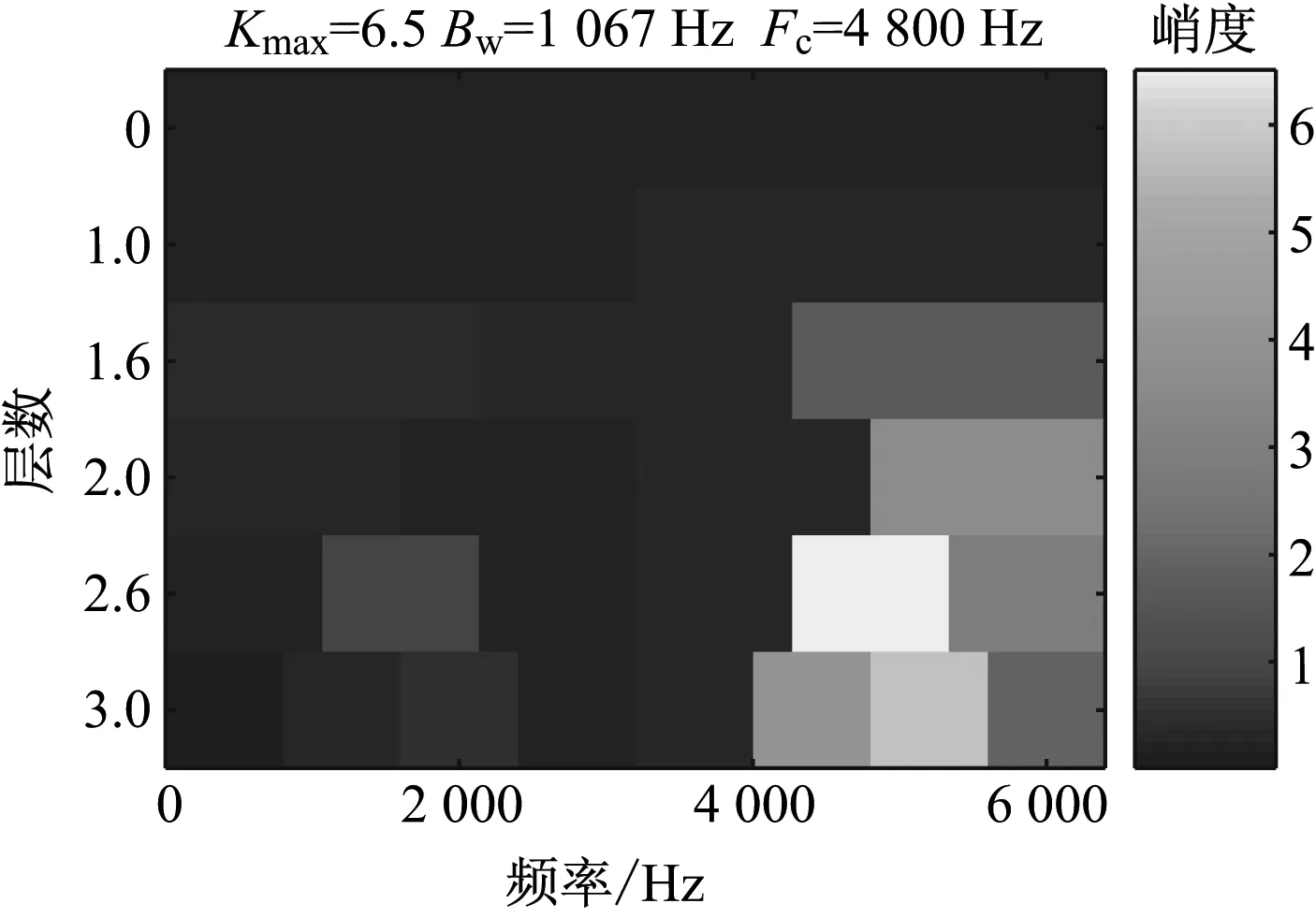
图20 采用快速峭度图法对轴承滚动体故障试验 信号进行处理后得到的峭度图

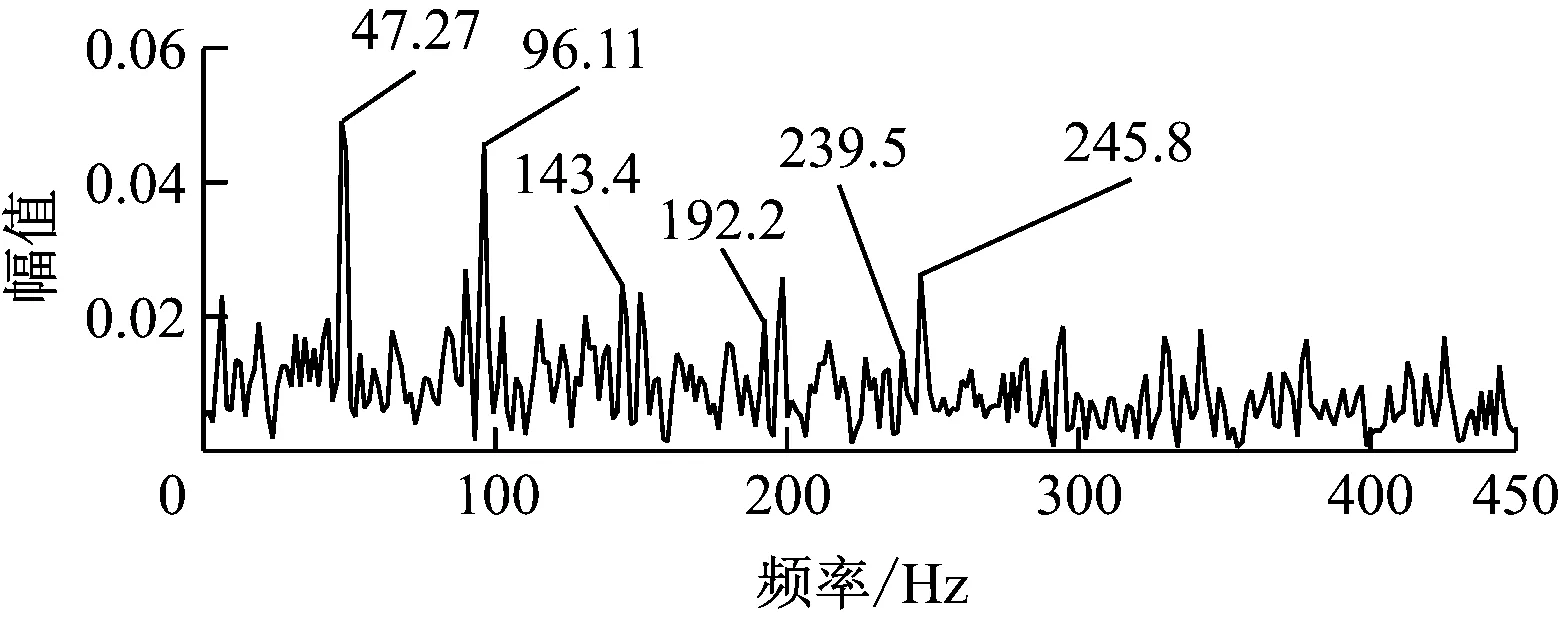
图21 采用快速峭度图法的轴承滚动体解调信号包络谱

6 结语

在低信噪比和非高斯噪声存在等情况下，快速峭度图不能充分提取脉冲信号信息，针对这一问题，提出了利用特定频带信号包络的功率谱幅值的峭度来量化由轴承局部故障引起的冲击脉冲，进而识别由局部损伤激起的共振频带。通过轴承故障仿真信号和试验信号验证了改进的峭度图法对提取轴承故障特征信息的有效性。通过与快速峭度图法进行对比分析，发现采用功率谱幅值的峭度能够有效避免背景噪声和随机干扰脉冲对时域峭度的干扰，从而提高了识别共振频带的准确率和提取脉冲信号的能力。