聚焦主题，突出重点：统计开放题的解答策略

葛 媛

（作者单位：江苏省南通市第一初级中学）

统计解答题中常常设计一些开放式问题，这类问题的答案不唯一，需要同学们根据题意简明作答，但注意回答时需聚焦主题，突出重点。以下面两题为例，讲解思路。

例1 某网站刊登了一则广告，“某种品牌的节能灯的合格率为95%”，请据此回答下列问题。

（1）这则广告是否说明市面上所有这种品牌的节能灯恰有5%为不合格？

（2）你认为这则消息来源于普查，还是抽样调查？为什么？

（3）如果已知在这次检查中合格产品有76个，则共有多少个节能灯接受检查？

（4）你以后面对这样的广告，要用怎样的数学眼光来看待它们？

【解析】（1）不能说明。

（2）消息来源于抽样调查。因为各种节能灯太多，很难实现普查。

（4）答案不唯一，可以基于抽样调查或样本代表性等角度进行阐述。比如，继续查阅该品牌节能灯的详细指标，如合格率是相对于怎样的抽样调查得到的，所选取的样本是否具有代表性，或者与其他品牌节能灯的同类指标进行对比。

例2 某中学高一（6）班共54名学生，经调查其中40名学生患有不同程度的近视眼病，初患近视眼病的各年龄段频数分布表如下：

（注：表中2岁～5岁的意义为大于等于2岁并且小于5岁，其他类似）

（1）求a的值，并把下面的频数分布直方图补充完整：

（2）从上面的直方图中你能得出什么结论（只限写出一个结论）？你认为此结论反映了什么社会问题？

【解析】（1）a=40-（3+4+13+6）=14；

频数分布直方图补充如下：

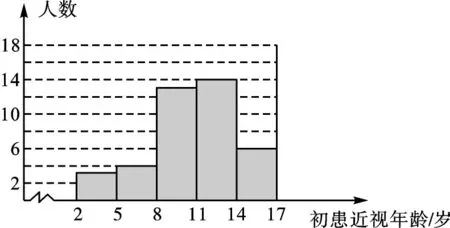
（2）本题答案不唯一。例如：调查结果表明，目前小学高年级、初中阶段的学生眼睛近视的比例大幅增加，一方面应引导学生重视用眼卫生，保护眼睛；另一方面，说明学生在小学高年级、初中阶段的学习压力过大，需要全社会都来关注这一问题；等等。

解后回顾：开放问题渐成新宠，解答时要注意聚焦主题，突显学科特点，特别是要针对题目所考查的知识点、数学概念进行阐释和作答，这样就可以尽可能争取得分点，切忌泛泛而谈、言不及义。