分层推进感悟思想
———《因数与倍数》教学
吴 亮
【教学内容】
苏教版五年级下册第30~32 页例1、例2、例3、“试一试”、“练一练”、练习五第1、2、4 题。
【教学过程】
一、揭示课题,明确学习内容
师:同学们,今天这节课我们一起学习因数与倍数。(板书课题)
二、借助素材,建构意义
1.出示例1。
师:用12 个同样大的正方形拼成一个长方形。每排摆几个,摆了几排?作为五年级的学生,同学们你们能不能挑战一下自己,在头脑中想象着拼一拼,并用一道乘法表示你的拼法呢?
(学生说如何拼,教师结合课件随机演示这三种拼法)
2.结合乘法算式,初识因数和倍数。
师:刚刚同学们用12 个同样大的正方形拼成了三种不同的长方形,由此还得到了三道不同的乘法算式。那么,在这些乘法算式中蕴藏着怎样的数学知识呢?
师:先来看第一道乘法算式,4×3=12,我们就说4 是12 的因数,3 也是12 的因数;也就是说4 和3都是12 的因数。反过来,12 是4 的倍数,12 也是3的倍数。其余的两道乘法算式,你也能像这样说一说哪个数是哪个数的因数,哪个数是哪个数的倍数吗?
(学生根据其余的两道乘法算式说一说)
师:同学们有没有发现,12 与它本身的关系很特别?
(引导学生发现12 既是12 的因数,也是12 的倍数)
师:能不能说12 是因数或者12 是倍数?
(学生讨论后明确:因数和倍数指的是两个数之间的关系,不能单独存在。另外,我们研究因数与倍数时,所说的数一般指不是0 的自然数)
3.结合除法算式,再识因数和倍数。
师:刚才我们通过拼长方形,根据列出的乘法算式认识了因数与倍数。那除了根据乘法算式,我们还能根据什么算式来描述两个数之间存在的因数与倍数关系呢?
出示“练一练”第一题。

同桌两人互相说一说,再全班交流。
小结:无论是乘法算式还是除法算式,都能帮助我们找到两个数之间存在的因数与倍数关系。
4.灵活运用,内化意义。
出示:5、9、10、36 四个数。
师:现在没有算式了,你还能找到两个数,说出哪个数是哪个数的因数,哪个数是哪个数的倍数吗?
(学生独立思考后,全班交流,交流的时候说一说自己的依据)
三、探索方法,发现特征
1.自主探究,找一个数的因数。
(1)出示例2。
师:通过刚刚的学习,同学们认识了因数与倍数。刚才,有同学提到9 是36 的因数,那除了9 以外,36 还有其他因数吗?
(学生分别说出几个36 的因数,并说一说是怎么找到的)
师:我们既可以利用乘法算式,也可以利用除法算式来找36 的因数,那36 的因数到底有哪些呢,你能想办法找到36 的所有因数吗?
(学生自主探索找36 所有因数的方法,教师巡视)
(交流展示学生作品,通过比较让学生发现有序地写出或想出所有符合条件的算式,再一组一组写出36 的所有因数,就可以不重复、不遗漏)
追问:36 里的因数里为什么没有5?
再问:为什么因数写到6 就不写下去了?
借助数形结合来研究列举36 的因数时从什么开始想起,从什么结束的问题。

师:其实列举出36 的所有因数还可以这样写:先从1 开始想起,找到1 和36 这一对,1 写在最前面,36 写在最后面。再找到2 和18 这一对,2 写在1的后面,18 写在36 的前面。同学们,你们能这样一组一组再继续写下去吗?
(学生把36 剩余的因数填写完整,核对后明确两个相同的因数6 只要写一个)
师:同学们请看,这样写就把36 的所有因数按照从小到大的顺序排列了起来。这样,不仅列举的过程是有序的,呈现出的结果也是有序的。
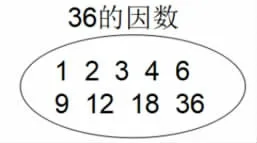
师:另外,36 的因数也可以用这样的集合圈表示:
(2)找15 和16 的因数。
师:刚才我们有序地找到了36 的所有因数,同学们想不想再来找一找一些数的因数?
(学生独立列举出15 和16 的所有因数后,指名两位同学上黑板写一写,并说一说列举的过程)
(3)观察比较。
师:刚才,我们通过有序地列举找出了这三个数的所有因素,请同学仔细观察比较一下这几个例子,说一说一个数的因数有什么特点?
(学生观察比较后,全班交流)
明确:一个数最小的因数是1,最大的因数是它本身;一个数的因数的个数是有限的……
(4)运用特征。
出示“练一练”第2 题,学生独立完成,集体核对。
2.小组活动,找一个数的倍数。
师:关于一个数的因数,我们暂且研究到这里。接下来,你们还想研究什么?
出示小组“研究单”

(1)写一写:小组里的四个人,每人想一个数,用列举的方法找出这个数的倍数。(2)说一说:在小组内交流自己找一个数的倍数的方法。(3)议一议:观察本小组找的几个数的倍数,看看有什么发现。
全班交流,明确:一个数最小的倍数是它本身,没有最大的倍数;一个数的倍数的个数是无限的……
3.回顾小结,总结经验。
师:回顾刚刚的学习过程,我们是怎么找一个数的因数和倍数的?在找的过程中要注意些什么?
小结:不管是找一个数的倍数,还是找一个数的因数。我们都要按照一定的顺序列举,这样就能做到不重复、不遗漏。
四、综合练习,提升能力
1.出示练习十五第4 题。
学生独立圈一圈,全班交流,发现:一个数本身既是这个数的因数,也是这个数的倍数。
2.出示练习十五第1、2 题。
学生独立填表后,说一说是根据怎样的数量关系来填表的。
引导学生观察比较。
提问:为什么每排的人数和排数都是总人数的因数;一共应付的元数是每人应付元数的倍数?
小结:只要题目中的数量关系满足a×b=c,那么a 和b 都是c 的因数,c 是a 和b 的倍数。
五、全课总结,回顾反思
师:今天这节课,你有什么收获?

