培养策略意识提升思维能力———《解决问题的策略（线段图）》教学设计

季正伟

【教学内容】

苏教版四年级下册笫48～49页例1、“练一练”，第52 页练习八第1～4 题。

【教学过程】

一、情境激趣，唤醒经验

师：老师这里有一幅数学上的图，谁能看懂？

小结：像这样的图叫做“线段图”，今天我们一起研究画线段图这种解决问题的策略。

【设计意图：让学生体会到图的直观、清楚，体会数学学习的价值。】

二、激发需要，感受策略

师：小春和小宁都是邮票爱好者，他们在集邮的过程中遇到了一些数学问题，我们一起来看看。

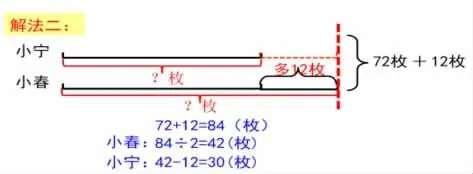
出示：小宁和小春一共有72枚邮票，两人邮票数量相等，两人各有邮票多少枚？能解决这个问题吗？

改变信息：“两人邮票数量相等”改为“小春比小宁多12 枚”。

师：这个问题和刚才的问题相比，你有什么感觉？到底这个问题难在哪里呢？

师：现在两人邮票数量不相等，数量关系变得复杂了。想一想，我们可以用什么方法能直观形象地表示出两人邮票数量之间的关系，以便我们分析问题呢？

【设计意图：从学生已有的经验入手，引入新知，加强新旧知识间的联系，唤醒经验，产生画图策略的需要。】

三、合作交流，探究策略

1.尝试画图，感知策略。

师：怎么画线段图整理信息呢？在脑子里先想一想，该先画什么？再画什么？

尝试：有想法了吗？在学习单上先尝试画一画。

介绍：我们掌声有请这位同学说一说是怎么画线段图表示题意的。

点评：画得怎么样，谁来点评点评？

小结：画线段图整理信息，既要画出条件，还要标注问题。

示范：下面伸出手和老师一起再来画一画。（指导括线的画法）

追问：为什么先画小宁的？

小结：看来画线段图时，跟谁比，先画谁，也就是先画作为标准的数量。

修改：请大家根据黑板上的线段图快速修正你所画的图。

复述：如果把文字先隐去，现在谁能对照线段图，说一说题意？

比较：要解决这个问题，你准备看文字，还是准备看线段图？

2.解决问题，体验策略。

（1）独立解决。

师：先仔细观察线段图列式解答，再和同桌交流。

（学生解答，教师巡视，指名板演）

（2）交流汇报。

师：下面我们一起来听听这些同学的想法。

方法一：

用总枚数减12 枚，就是小宁邮票枚数的2 倍，可以先求小宁的枚数，再求小春的枚数。

预设1：结合图说。

师：这位同学的介绍好在哪里？听明白的举手？找个懂你的人再来说一说。

预设2：没有结合图说。

师：写了这么多算式，老师好像还没明白，谁再来教教我？

师：你一边指着图，一边介绍算式，我听懂了，谢谢你。这么多的算式，你们是根据什么思考得出的？哪些同学也是这样做的？

方法二：

用总枚数加1 2 枚，就是小春邮票枚数的2 倍，可以先求小春的枚数，再求小宁的枚数。

追问：你们都明白了吗？你们是根据什么思考得出的？

动画演示：好方法值得回味，我们一起看大屏幕再来体会体会。

追问：为什么减12，（让小春变得和小宁一样多）总数怎么变，先算出什么？再算出什么？

为什么加12，（让小宁变得和小春一样多）总数怎么变，先算出什么？再算出什么？

方法三：（拓展）

师：要使两人邮票同样多，还可以怎么办？

（3）比较沟通。

师：虽然这三种方法不一样，但有一样的地方吗？

小结：虽然方法不一样，但是都是使两人的邮票同样多，这是解决问题的关键。

追问：同学们，你们太厉害了，原来都说难，现在竟然找到了三种不同的思路和方法，你觉得都是谁的功劳。它又不会说话，怎么帮你们了?

小结：线段图不仅可以直观、形象地表示信息，还能表示数量关系，启迪我们思考。

（4）检验答案。

师：答案对不对呢？我们还需要进行检验。

预设1：看看两人的邮票总数是不是72 枚。（30+42=72 枚）

预设2：还要检验小春是不是比小宁多12 枚。（42-30=12枚）

小结：把得数代入原题看看符合所有已知条件是一种常见的检验方法。两种方法也可以互相检验。

【设计意图：自主探究、合作交流都是重要的学习方式，本环节充分让学生先思考后交流，让学生体会解决问题的策略不同于解决问题的方法，方法可以在传递中习得，但策略却不能从外部直接输入，只能在体验中感悟、内化。通过比较沟通，学生依据自己实施的策略在头脑中拟出问题解决的具体操作程序，同时真正体会画图策略的重要性，将画图策略内化。】

四、回顾反思，建构策略

师：我们一起回顾刚才解决问题的过程，你有什么体会？

小结：当遇到比较复杂的问题，一时难以确定解题思路时，可以先画图表示题意，因为画线段图能使数量关系更直观、更清楚；根据线段图分析数量关系，更容易找到解题方法；把得数代入原题检验要符合所有已知条件。

【设计意图：让学生回顾学习的过程，帮助学生整理本节课基础知识的同时，有效促进知识结构的形成。】

五、巩固应用，内化策略

1.练一练。

师：这幅线段图，你能知道哪些信息？（图略）

快速算一算。

比较“练一练”和例1 有什么不同点和相同点？

不同点：多一些、少一些的画法不一样。

相同点：都是已知两个数量的和与差，求这两个数量的实际问题，解题时可以画线段图分析数量关系，都要想办法把两个不相等的数量转化为相等的数量。

2.试一试。

师：两个不相等的量我们能够变成相等的量来解决，想不想来点有挑战的？

出示：班级图书角上层和中层数量相等，下层比中层多12本，三层书架总共有132 本书，三层各有图书多少本？

3.想一想。

今天我们一起学习了画线段图的策略，其实线段图我们早已接触过。让我们跟着大屏幕一起来看看。

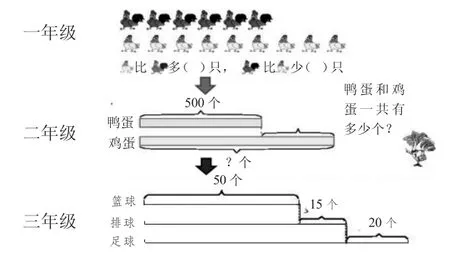
4.夸一夸。

师：今天谁对我们的帮助最大？请你来夸夸它。

文化渗透：看看数学家华罗庚怎么夸的，数形结合百般好，数形分离万事难。

【设计题图：通过多层次的变式练习，既巩固了新知，又发展了学生灵活运用新知分析问题、解决问题的能力。体现了人人学有价值的数学，不同的人在数学上得到不同的发展的思想。】

六、总结评价，提升策略

师：通过今天的学习，你有什么收获？

小结：画图的策略可以帮助我们更直观、清楚地理解题意，找到解决问题的办法。